マイナス×マイナスがプラスになることを説明するときに意識しておくこと

　数学の概念を分かりやすい言葉で説明しようとするときに、意識しなければならないことがあります。それは、抽象的な世界と現実世界との関係性です。

　例えば (-1) x (-1) = +1 という式は、抽象世界の存在です。

この式に関して、よく以下のような説明がされます。
「借金 (マイナス) がなくなる (マイナスを掛ける) とプラスになる」
これは数式 (-1) x (-1) = +1 が成り立つ理由ではなく、(-1) x (-1) = +1 という概念を「借金の論理」に応用したに過ぎません。

　一般的に、現実世界の事象の数学的な表現は、抽象世界で成り立つ事実を応用しているだけです。この、応用する側とされる側という関係を意識しておかないと、概念に間違った理由付けをおこなってしまいます。

　では、抽象世界にある数式が成り立つ理由を、現実世界に求めてはいけないかというと、すべてがそうではありません。それが意識すべきことの2つ目。「抽象世界は、現実世界からの動機付けがあって生まれる」ということです。

　再度「マイナスｘマイナス＝プラス」を例にとって説明します。

　負の数はもともと、欠けたり減ったりすることを表すために生まれたと考えられます。

　このとき、マイナス世界の加法は現実世界のイメージをそのまま投影して定義することができます。

このように、マイナスの数が生まれる部分では、現実世界が抽象世界の数式や性質に理由付けを与えています。

　抽象世界で理論が成熟してくると、マイナスの数も、プラスの数と同じように扱おうという流れが生まれ、マイナスの世界にも乗法を定義したくなります。そのとき、プラスの数の世界で成立していた分配法則などをマイナスの世界でも成り立つようにするのが自然です。

　このように性質を保ったまま概念を広げることをよく「拡張」と言ったりします。分配法則などの性質を保つ、という条件のもとでマイナスの数を扱おうとすると、必然的に「マイナス×マイナス＝プラス」がそれらの法則から導かれる「定理」となります。

　こうしてマイナスの概念は抽象世界の中で成長を続け、やがて整数の理論へと到達します。

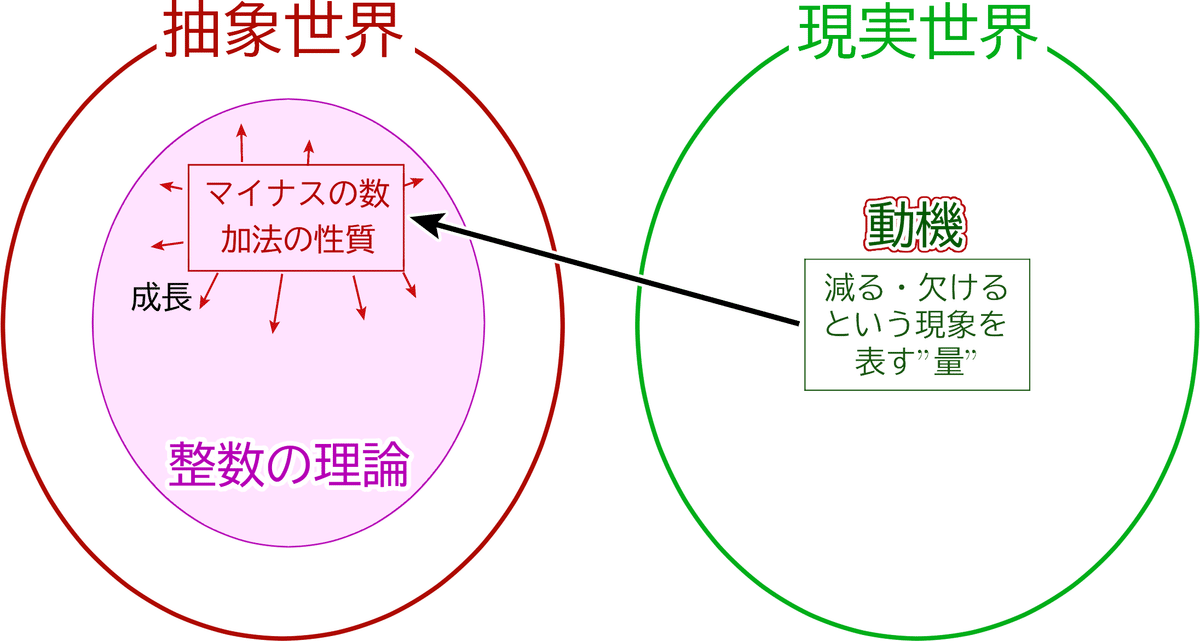
　そして、成長した世界で得られる結果「マイナス x マイナス=プラス」は、前述した「借金の論理」など、再び現実世界に応用できるものとなっています。

　(-a)+(-b)=-(a+b) などの加法に関する数式は、マイナスの世界が生まれる動機となった部分に近いため、現実世界に理由を求めてもいいといえます。

　しかし、マイナス数どうしの掛け算は、抽象世界で独自に成長を遂げた部分の数式のため、現実世界に理由を求めることが難しくなっています。

　このように、どこが現実世界からの動機づけとなっているのか、ということを意識して考えるようにすると、数式が成り立つ理由を明確にできます。

　※負の数の世界へ拡張する際、満たしてほしい法則を取捨選択し、分配法則や可換法則などのうち一部を無視したり、または全く別の自然数の法則を付け加えたりして概念を広げることも可能であり、その場合、わたしたちが知るマイナスとは異なる概念が生まれ、それが現実世界への応用を持つこともあり得ます。

次の記事では「虚数は存在するのか？」について、動機付けの観点から考察してみます。虚数は少し様子が違いそうです。