
図式で学ぶ線形代数 番外編 ~列ベクトルや行列での微分~
連載の記事一覧:
#1 図式の基礎と線形代数の基礎
#2 スペクトル分解と特異値分解
#3 テンソル積およびトレース・転置・内積
#4 行列が作るヒルベルト空間
番外編 列ベクトルや行列での微分
番外編その2 ベクトル解析
信号処理や機械学習などの分野では,列ベクトルや行列での微分を考えたくなるときがしばしばあります。このような微分の計算は,数式で考えるとやや煩雑に思えるのですが,本質的にはそれほど複雑ではありません。実際,図式で考えれば,いろいろな公式を楽に導出できるようになります。図式の威力を実感できるかもしれない活用例の一つとして,その方法をまとめておきます。
このような微分はいつ必要?
列ベクトルや行列での微分になじみのない人のために,ひとつ例を挙げておきます。行列 $${ A }$$ と列ベクトル $${ \ket{b} }$$ がわかっているときに
$$
A \ket{x} = \ket{b}
$$
を満たす $${ \ket{x} }$$ を求めたい(つまり連立1次方程式を解きたい)とします。このような問題は,さまざまな分野でしばしば登場します。この問題は,与えられた値 $${ \ket{b} }$$ から行列 $${ A }$$ の影響を受ける前の値 $${ \ket{x} }$$ を求めるという問題と解釈できます。実際の問題では,解が存在しなかったり,与えられた値 $${ \ket{b} }$$ にノイズが乗っている場合などが考えられます。この場合には,上記の式を直接解くことはもはや適切ではないでしょう。代わりに,例えば
$$
f(\ket{x}) \coloneqq \| A \ket{x} - \ket{b} \|_2^2
$$
を最小とするような $${ \ket{x} }$$ を求めるといった問題を考えたくなります。このとき,$${ f(\ket{x}) }$$ の極小値を求めるために $${ f(\ket{x}) }$$ を $${ \ket{x} }$$ で微分した値が $${ 0 }$$ になるような $${ \ket{x} }$$ を求めたくなることでしょう。この $${ \ket{x} }$$ での微分が「列ベクトルでの微分」にほかなりません。同様に,$${ f }$$ が列ベクトルではなく行列の関数として表される場合には,「行列での微分」を考えたくなると思います。
微分の定義
この記事では,実ベクトルや実行列を考えます(複素空間は考えません)。
まず,スカラーの行列での微分を考えます。$${ m \times n }$$ 実行列 $${ X \in \R^{m \times n} }$$ を $${ f(X) \in \R }$$ に写す写像 $${ f:\R^{m \times n} \to \R }$$ を考えます。$${ X }$$ の $${ (i,j) }$$ 成分を $${ X_{i,j} }$$ とおきます。$${ \frac{\partial}{\partial X} f(X) }$$ は,$${ \frac{\partial}{\partial X_{i,j}} f(X) }$$ を $${ (i,j) }$$ 成分とする $${m \times n}$$ 実行列,つまり
$$
\frac{\partial}{\partial X} f(X) \coloneqq
\begin{bmatrix}
\frac{\partial}{\partial X_{1,1}} f(X) & \frac{\partial}{\partial X_{1,2}} f(X) & \cdots & \frac{\partial}{\partial X_{1,n}} f(X) \\
\frac{\partial}{\partial X_{2,1}} f(X) & \frac{\partial}{\partial X_{2,2}} f(X) & \cdots & \frac{\partial}{\partial X_{2,n}} f(X) \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial}{\partial X_{m,1}} f(X) & \frac{\partial}{\partial X_{m,2}} f(X) & \cdots & \frac{\partial}{\partial X_{m,n}} f(X) \\
\end{bmatrix}
$$
として定義されます。
特に $${ n = 1 }$$ の場合には $${ X }$$ は列ベクトルになり(この $${ X \in \R^m }$$ を改めて $${ \ket{x} }$$ とおきます),微分は次のように表されます。
$$
\frac{\partial}{\partial \ket{x}} f(\ket{x}) =
\begin{bmatrix}
\frac{\partial}{\partial x_1} f(\ket{x}) \\
\frac{\partial}{\partial x_2} f(\ket{x}) \\
\vdots \\
\frac{\partial}{\partial x_m} f(\ket{x}) \\
\end{bmatrix}
$$
ただし,$${ x_i }$$ は $${ \ket{x} }$$ の $${ i }$$ 行目の成分です。
次に,行列の行列での微分を考えます。$${ f }$$ を $${ \R^{m \times n} }$$ から $${ \R^{m' \times n'} }$$ への写像とします。このとき,$${ X \in \R^{m \times n} }$$ に対して $${ f(X) \in \R^{m' \times n'} }$$ です。この場合にも $${ \frac{\partial}{\partial X} f(X) }$$ を上と全く同じ式で定義できます。ただし,この場合には各 $${ \frac{\partial}{\partial X_{i,j}} f(X) }$$ は $${ m' \times n' }$$ 行列であり,したがって $${ \frac{\partial}{\partial X} f(X) }$$ は $${ mm' \times nn' }$$ 行列です。なお,文献によっては上記の定義とは行列の成分の並び方などが異なる場合がありますが,本質的な違いはありません。
微分の図式
図式において,$${ \frac{\partial}{\partial X} f(X) }$$(ただし $${ X \in \R^{m \times n} }$$ および $${ f(X) \in \R^{m' \times n'} }$$)を次のように表すことにします。

$${ X }$$ には依存しない行列 $${ A }$$ については,明らかに $${ \frac{\partial}{\partial X}A = 0 }$$ が成り立ちます。また,$${ \frac{\partial}{\partial X_{i,j}}X_{k,l} = \delta_{i,k} \delta_{j,l} }$$ より

が成り立つことがわかります。特に $${ n = 1 }$$ の場合には次式が成り立ちます。

基本的な規則
微分について成り立ついくつかの基本的な規則と,対応する図式を示します。
(1) 和の保存:$${ \frac{\partial}{\partial X}[f(X)+g(X)] = \frac{\partial}{\partial X}f(X) + \frac{\partial}{\partial X}g(X) }$$

(2) 積の法則:$${ \frac{\partial}{\partial X}[f(X)g(X)] = [\frac{\partial}{\partial X}f(X)]g(X) + f(X)[\frac{\partial}{\partial X}g(X)] }$$
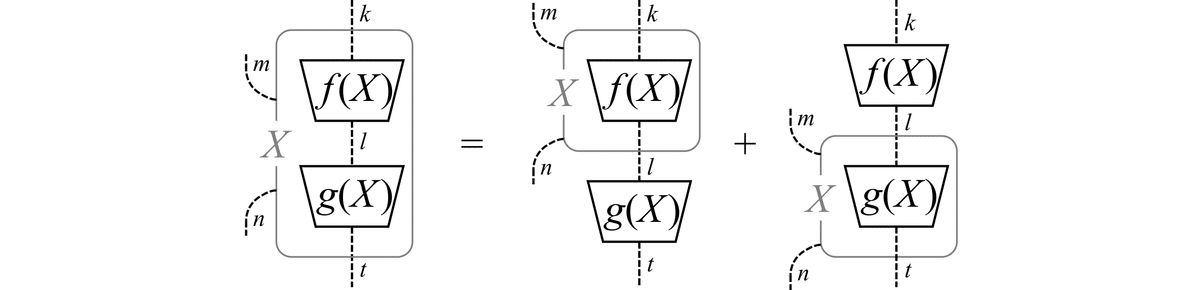
(3) テンソル積の法則:$${ \frac{\partial}{\partial X}[f(X) \otimes h(X)] = [\frac{\partial}{\partial X}f(X)] \otimes h(X) + f(X) \otimes [\frac{\partial}{\partial X}h(X)] }$$

なお,図式では右辺のテンソル積の順序が第1項と第2項で異なっていますが,本質的ではないため気にしないことにします(交換行列を適当に施せば容易に順序をそろえられます)。
(4) 連鎖律:$${ \frac{\partial}{\partial X}f[Y(X)] = \bra{\cap_k} \frac{\partial}{\partial X}Y(X) \otimes \frac{\partial}{\partial Y}f(Y) \ket{\cup_l} }$$

具体例
これまでに述べた図式を組み合わせると,行列での微分に関するさまざまな公式を導けます。以下に,いくつかの例を示します。なお,第3回で述べたような「cup列ベクトルやcap行ベクトルに関する基本的な規則」を用いますが,これらの規則を知らない人でも何となく理解できるのではないかと思います。
列ベクトルでの微分
(1) $${ \frac{\partial}{\partial\ket{x}} \braket{a|x} = \ket{a} }$$

(2) $${ \frac{\partial}{\partial\ket{x}} \braket{x|A|x} = (A + A^\mathrm{T}) \ket{x} }$$

$${ \bra{x} }$$ は180度回転させて $${ \ket{x} }$$ に置き換えてから微分します。2行目の最初の等号では,上で述べた「和の保存」の規則を用いています。
(3) $${ \frac{\partial}{\partial\ket{x}} \| A \ket{x} - \ket{b} \|_2^2 = 2A^\mathrm{T} (A \ket{x} - \ket{b}) }$$
$${ \| A \ket{x} - \ket{b} \|_2^2 = (A \ket{x} - \ket{b})^\mathrm{T} (A \ket{x} - \ket{b})}$$ を展開して上記の(1),(2)を用いればすぐに得られます(確かめてください)。これで,本記事の冒頭で述べた問題を扱えるようになりました。
行列での微分
(1) $${ \frac{\partial}{\partial X}\braket{a|X|b} = \ket{a} \bra{b} }$$
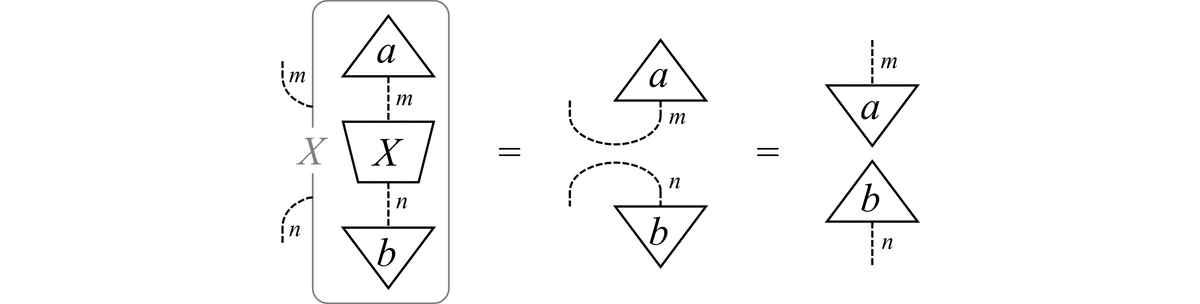
(2) $${ \frac{\partial}{\partial X}\mathrm{Tr}(AX) = A^\mathrm{T} }$$

(3) $${ \frac{\partial}{\partial X}\mathrm{Tr}(AXBX) = A^\mathrm{T}X^\mathrm{T}B^\mathrm{T} + B^\mathrm{T}X^\mathrm{T}A^\mathrm{T} }$$

(4) $${ \frac{\partial}{\partial X}\mathrm{Tr}(XX^\mathrm{T}) = 2X }$$

$${ X^\mathrm{T} }$$ は180度回転させて $${ X }$$ に置き換えてから微分します。
さらなる情報
詳細やその他の具体例に興味がある人は,次の論文をお読みください(図式が多いので英語を読まなくても楽しめると思います)。
また,この論文の内容を含んだ資料を記事「図式で学ぶ線形代数 番外編2 ~ベクトル解析~」の最後のほうからダウンロードできます。
この連載は,書籍「図式と操作的確率論による量子論」の内容の一部を紹介したものです(この記事のほうが詳しく述べている箇所もあります)。
