図式で学ぶ線形代数 #2 ~スペクトル分解と特異値分解~
連載の記事一覧:
#1 図式の基礎と線形代数の基礎
#2 スペクトル分解と特異値分解
#3 テンソル積およびトレース・転置・内積
#4 行列が作るヒルベルト空間
番外編 列ベクトルや行列での微分
番外編その2 ベクトル解析
この連載では,図式とよばれる式を用いて線形代数を説明しています。第2回目では,正規行列とスペクトル分解について説明します。また,スペクトル分解の拡張版といえる特異値分解についても述べます。
線形代数の書籍では,ユニタリ行列・エルミート行列・半正定値行列などがよく登場しますが,これらはすべて正規行列です。正規行列について学ぶことで,これらの行列を体系的に習得できると思います。
前回の復習
前回の記事では,行列をブロックで表現するような図式を紹介しました。列ベクトル・行ベクトル・スカラーは行列の特別な場合とみなすのでした。
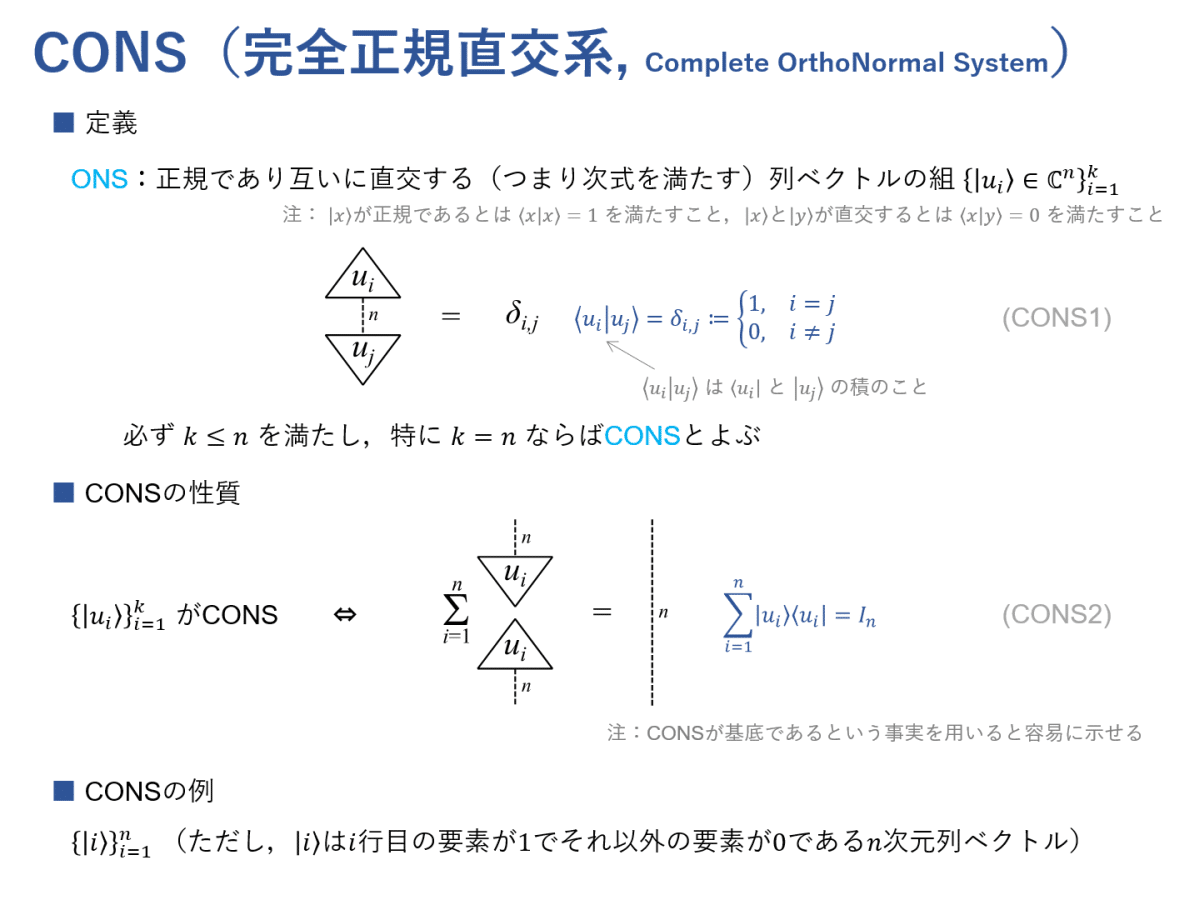
今回は,前回の記事で述べたCONS(完全正規直交系)の性質をよく用いますので,関連するスライドを再掲しておきます。
正規行列とスペクトル分解
以下では,複素行列を考えます。

正規行列の定義を示しています。また,正規行列であることはスペクトル分解できることに等しいことを主張しています。ここで,行列 $${X}$$ のスペクトル分解とは,複素数 $${\lambda_1,\dots,\lambda_n}$$ とCONS $${ \{ \ket{u_i} \}_{i=1}^n }$$ を用いて
$$
X = \sum_{i=1}^n \lambda_i \ket{u_i} \bra{u_i}
$$
の形で表すことです。なお,この命題の証明はここでは省略しますが,それほど難しくありません。本書(=今秋出版予定の書籍)に記載しています。

ユニタリ行列・エルミート行列・(半)正定値行列・射影行列の定義を表にまとめています。これらはすべて正規行列であり,固有値により分類できます。
エルミート行列・ユニタリ行列・射影行列が正規であることはすぐに確認できます。一方,半正定値行列が正規であることはすぐにはわからないかもしれませんので,後で証明します(それほど難しくはありません)。
念のため,実ベクトル空間の場合について少し補足しておきます。この場合,行列として実行列(つまりすべての成分が実数である行列)を考えることになります。複素ベクトル空間の場合と同じく式(Spec)の形で表すことをスペクトル分解とよびますが,通常は $${\lambda_1,\dots,\lambda_n}$$ や $${ \ket{u_1},\dots,\ket{u_n} }$$ のすべての成分が実数であるという制約が課せられます。この制約のため,上で示した複素ベクトル空間の場合の表とは少し様子が変わります。例えば,スペクトル分解できるのはエルミート行列に限られますし,ユニタリ行列は(それがエルミートでない限り)スペクトル分解できなくなります。また,半正定値行列の定義として,複素ベクトル空間の場合と同様に
$$
\braket{x|S|x} \in \R_{\ge 0} ~(\forall \ket{x} \in \R^n ) \quad (1)
$$
を満たすような行列 $${ S }$$ を半正定値行列とよびたいところですが,このように定義するとエルミートではない半正定値行列が存在することになります(これでは都合が悪いことが多いため,上記の式(1)を満たす行列のうちさらにエルミートであるものを半正定値行列と定義することが一般的なようです)。実ベクトル空間でも複素ベクトル空間でも,このような多少の違いはありますが多くの共通点があり,これから述べることの大半は実ベクトル空間にもそのまま適用できます。なお,エルミートである実行列は対称行列,ユニタリである実行列は直交行列ともよばれます。

先ほど表で示した行列たちの包含関係を示しています。

正規行列の捉え方を述べています。
$${ X\ket{u_j} = \lambda_j \ket{u_j} }$$ は,$${ X }$$ と列ベクトル $${ \ket{v} \in \Complex^n }$$ の積 $${ X \ket{v} }$$ を求める際にもしばしば利用できます。具体的には,
$$
\ket{v} = \sum_{i=1}^n v_i \ket{u_i}, \quad v_i \coloneqq \braket{u_i|v}
$$
が成り立ちますので
$$
X\ket{v} = \sum_{i=1}^n X v_i \ket{u_i} = \sum_{i=1}^n \lambda_i v_i \ket{u_i}
$$
です。これは,「列ベクトル $${ \ket{v} }$$ に $${ X }$$ を掛けることは各 $${ \ket{u_i} }$$ に対する係数 $${ v_i }$$ を $${ \lambda_i v_i }$$ に変えることに等しい」と解釈できます。

半正定値行列はエルミート行列(したがって正規行列)であることを示します。

正規行列同士のテンソル積は正規行列です。ユニタリ行列同士のテンソル積はユニタリ行列です。エルミート行列などについても同様です。

$${ H }$$ がエルミートならば,任意の行列 $${ X }$$ に対して $${ XHX^\dagger }$$ はエルミートです。半正定値行列についても同様です。

2組のCONSからユニタリ行列を作れます。逆に任意のユニタリ行列は2組のCONSに分解できます。CONSは直交座標系のことですので,ユニタリ行列はある直交座標系を別の直交座標系に変換するような写像とみなせます。

ユニタリ行列の定義より,$${ n }$$ 次正方行列 $${ U }$$ がユニタリであることは $${ U^\dagger U = I_n = U U^\dagger }$$ を満たすことと等価です。ここでは,単に $${ U^\dagger U = I_n }$$ を満たすこととも等価であることを示しています。このため,$${ n }$$ 次正方行列 $${ U }$$ が $${ U^\dagger U = I_n }$$ を満たすならば $${ U U^\dagger = I_n }$$ を満たします。
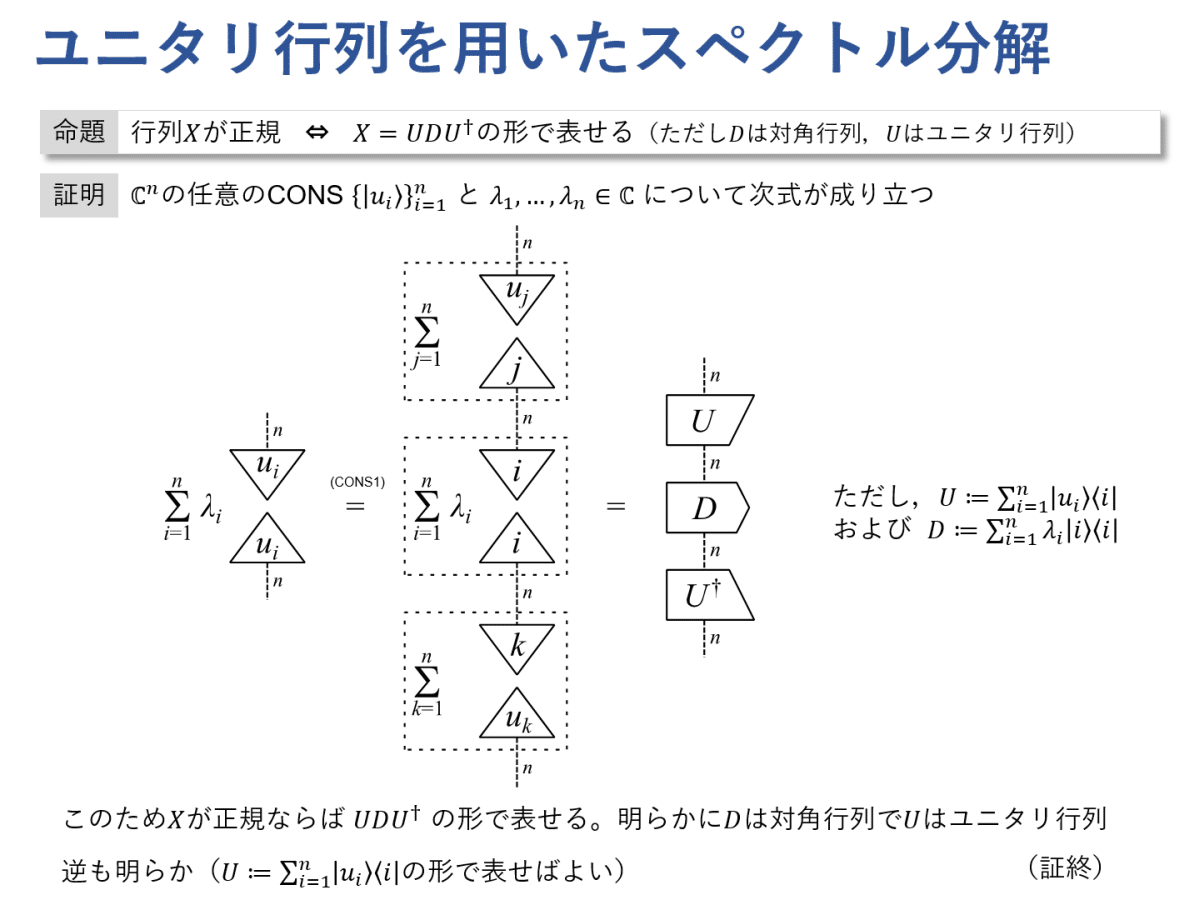
スペクトル分解はユニタリ行列と対角行列を用いて表すこともできます。この表現は,式(Spec)による表現と本質的には同じです。

半正定値行列は $${ XX^\dagger }$$ の形で表せます。この形で表すと便利な場面がしばしばあります。

スペクトル分解を用いれば,正規行列 $${ X }$$ に対して $${ X^k }$$($${ k }$$ は任意の自然数)を容易に求められます。この性質を利用することで,$${ \sqrt{X} }$$ や $${ \exp(X) }$$ といった「正規行列の関数」を自然な形で定義できます(テイラー展開やマクローリン展開を知っている方は,ここで示した命題を用いれば容易に推測できるかと思います)。正規行列の関数はさまざまな場面に応用できて,慣れると便利です。なお,正規とは限らないより一般の行列 $${ X }$$ に対しても $${ f(X) }$$ を定義できるのですが,本記事では割愛します。
特異値分解

スペクトル分解は正規行列のみに対して行えますが,任意の行列に適用できるように拡張したもの(の一つ)が特異値分解といえます。
なお,スペクトル分解の拡張とみなせるような分解は,特異値分解のほかに固有値分解(対角化)・三角化・ジョルダン分解などがあります(本記事では扱いません)。これらの分解は用途に応じて使い分けるのがよいと思いますが,量子論では特異値分解が比較的多く用いられるような気がします。
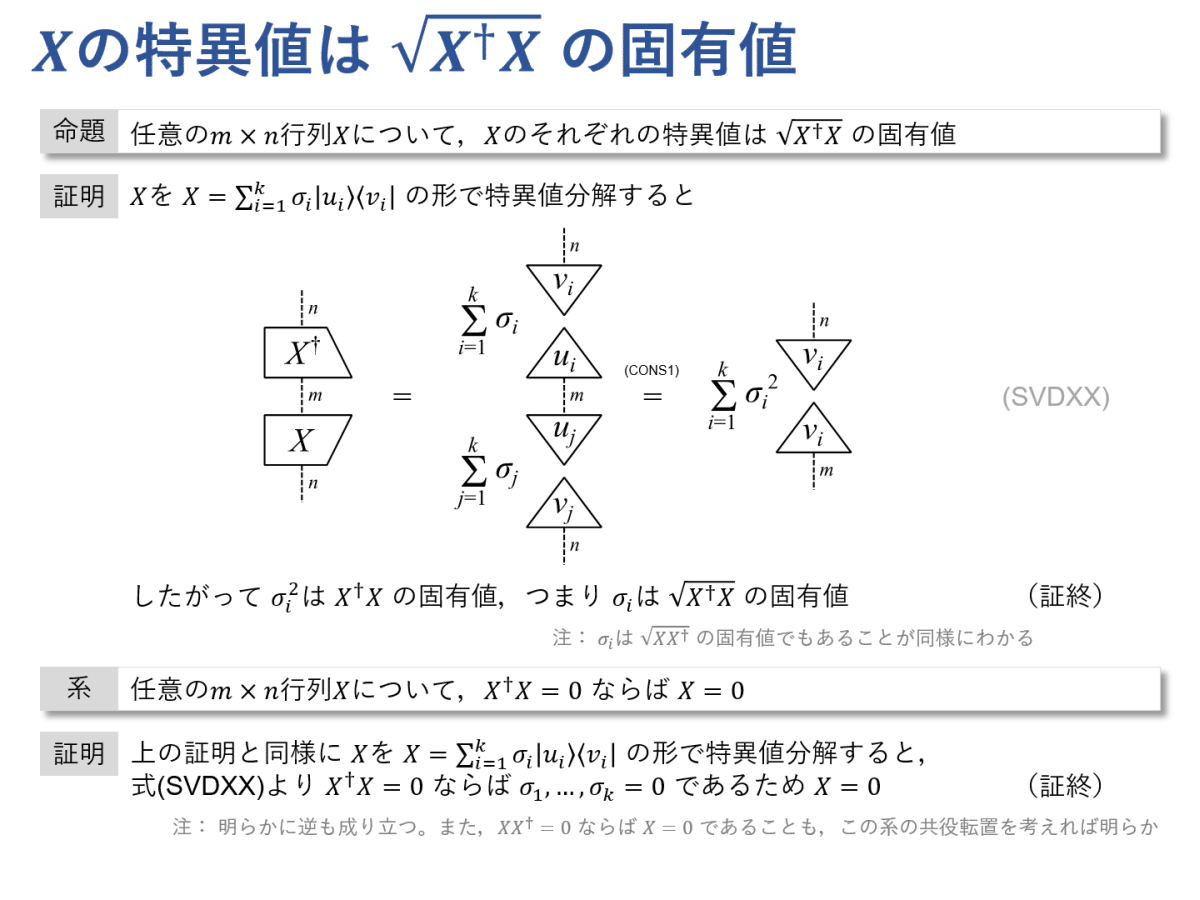
$${X}$$ の特異値は $${ \sqrt{X^\dagger X} }$$ の固有値(つまり $${ X^\dagger X }$$ の固有値の非負の平方根)です。$${ X^\dagger X }$$ は半正定値ですので,$${ \sqrt{X^\dagger X} }$$ を定義できます。

正則行列 $${ X }$$ に対して,$${ X^{-1} }$$ の特異値分解は $${ X }$$ の特異値分解からすぐに得られます。

特異値分解の式を少しだけ変形すると極分解とよばれる形になります。この分解は,複素数の極形式表現を正方行列に拡張したものといえます。
今回は正規行列がスペクトル分解できる行列であることに等しいことを述べ,正規行列の主要な性質について説明しました。また,特異値分解についても触れました。
次回は,cup列ベクトルやcap行ベクトルを導入してトレースや内積を表現する方法について説明する予定です。次回から,図式の威力が発揮されることになると思います。
この記事は,書籍「図式と操作的確率論による量子論」の内容の一部を紹介したものです(この記事のほうが詳しく述べている箇所もあります)。
