STEMA／STEAM教育とリベラルアーツまたは数学

最近、日本ではSTEMA（またはSTEAM）教育の強化が叫ばれている。背景はAIやデータサイエンス、IT人材の不足があるのだろう。しかし、英語力強化も含め教える側の教師の待遇改善、リスキリングをやらないと、タブレットやPCを使った電子教材によるカバーだけでは限界があるのではないか。現場はどうなのであろうか。

STEMAは、Aを除くSTEMの①Science②Technology③Engineering④Mathematicsまでは間違いない。見てわかるように①～④は厳密に分けられるものではない。例えば数学は科学の一部（或いは基礎）であろうし、テクノロジーとエンジニアリングの切分けがどこか曖昧である。最も、STEMは米国由来の用語なので今更日本でどうこういうものではないだろう。

よく分からないのがAである。ざっと調べたところ英語サイトには出てこないので日本でつけたのだろうと思われる。A=Artだと思っていたが、文科省のサイトを見たところ、「Aの範囲を芸術，⽂化のみならず，⽣活，経済，法律，政治，倫理等を含めた広い範囲（Liberal Arts） で定義し，推進することが重要である」とあった。
本来は理数系の教育強化を主眼としていたはずなのに、これでは何でもかんでも入れ過ぎではないかと思う。STEM＋芸術に偏ることなくバランスよく学ぶべきことは当たり前なで、敢えて入れる必要もないだろう。Liberal Artsという用語を使っているのも違和感が否めない。リベラルアーツの対象とは何か、日本に限ったとしても合意形成ができるとは思えない。また、文化や生活といっても広すぎてよく分からないのではないか。
補足：
元々のリベラルアーツは「自由に思考するための技法」「自由人として身につけるべき技法」等の意味の西欧生まれのもので、文法、修辞学、弁証法、算術、幾何、天文学、音楽の所謂自由７科と呼ばれるものをいう。
古代ギリシャ以来、西欧の人々は論理を大変重要視したので、数学に変換できる音楽をリベラルアーツに入れたが（音楽＝音階を数学に変換した元祖はピュタゴラス？）、それができない美術は入れなかったのではないかと勝手に想像している。
＜2024/05/01追記＞
この日から池上彰さんが日経朝刊でSTEAM教育のコラムを担当することに
なった。やはりA=芸術と書いてあった。

さて、用語マターはさておき、STEMAの中で元も基本と思われるM=数学について少し書いてみる。数学と聞いただけで苦手という方もいるであろうが、特に難しい話は出てこない（はず）。趣旨としては計算問題だけでなく歴史的なことも教えればもっと算数・数学が好きになるのではと思えるからである（因みに自身は小学校・中学校の算数・数学は好きではなかった）。

1．インドのゼロの発見の意味とは？
インドでゼロ（0）が発見されたことはよく知られている。0とは記号としてのゼロと数字してのゼロがある。前者の記号としてのゼロは位取りのための記号と考えればよい。例えば48、408、480、4800は異なる数字であるが、この0を現代の筆算でやるような加減乗除の対象となる数字という意味ではなく「位取り」記号として用いていると考えるということだ。「0」という文字を位取り記号として使ったかどうかを無視すれば、記号としてのゼロの発見はインドがオリジナルではない。
＜補足＞
古代メソポタミア文明では周知のように楔形文字がつかれていたので実際の記法ではないが、48と408は「48」「4　8」のように間に間隔を空けるなど
して区別していた。

インドが発見したのは数字としてのゼロである。これにより「0」は位取り記号兼数字のゼロ（0）として使えるようになった。結局、負の数を含め、0，1，2，3，4，5，6，7，8，9だけを使って全ての数を表し、我々が行っている筆算が可能になったルーツはインドと言ってよい。それをアラビア人が発展させて西欧に伝えたことで現代はアラビア数字と言わている。インド・アラビア記数法というのが本来は妥当である。

2．もう一つのアルキメデスの原理
一般に言うアルキメデスの原理＝浮力の原理を知らない人はまず、いないであろう。物体にかかる浮力は、自分が押しのけた流体の重量＝自分の体積に相当する流体の重量であるという原理である。実はもう一つアルキメデスの原理というものがある。それは
「どんなに小さい数でも、それを何度も足し合わせていけば、いかなる大きな数をも超えることができる。」
である。理屈は省略するが、例えば、これによりお馴染み円の面積の公式

「半径がｒの円の面積S」

も証明している。

アルキメデスというと、上述の浮力の原理の風呂での発見譚や対ローマ軍向けの兵器（クレーン）の作成、船のスクリュー開発などのエピソードが有名なため、数学者の側面はあまり一般に知られていないと思う。ウィキペディアに「数学者、物理学者、技術者、発明家」と書いてあるよう、絵画を除けばレオナルド・ダ・ビンチに匹敵する？マルチな天才で数学（主に幾何学）に多大な貢献をしている。冒頭の画像は数学のノーベル賞と言われるフィールズ賞の受賞者に与えられるメダル＝フィールズ・メダルで、アルキメデスの横顔をレリーフしてある。

3．現在でも信じる人がいるゼノンの逆説
「ゼノンのパラドックス」というのがあるのはよく知られているであろう。「アキレスは亀に追いつけない」「飛んでいる矢は止まっている」のうち、前者の方が広く人口に膾炙していると思う。
「アキレスは亀に追いつけない」とは？
アキレスと亀がいて徒競走をすることとなった。アキレスの方が亀より足が速いのは明らかなので亀がハンディキャップをもらうことにして、いくらか進んだ地点Aからスタートすることとなった。
スタート後、アキレスが地点Aに達した時には、亀はアキレスがそこに達するまでの時間分だけ先に進んでいる（地点B）。アキレスが地点Bに達したときには、亀はまたその時間分だけ先へ進む（地点C）。同様にアキレスが地点Cの時には、亀はさらにその先にいることになる。この考えはいくらでも続けることができ、結果、いつまでたってもアキレスは亀に追いつけない。

大分前の調査によると、米国のキリスト教徒の半分弱位は旧約聖書の天地創造神話は事実と思っていてダーウィンの進化論を信じていないそうだ。これと同様、ゼノンのパラドックスも正しいと思っている人が多い（正しくないことの説明（証明）が困難だからか？）ということを聞いたことがある。今なら、極限・収束（日本では高校の数学で学ぶ）を使って正しくないことの証明は可能（多分容易？）なるも、それを使わないでどう反駁するか、古代ギリシャ～現代まで多くの著名な数学者、哲学者が意見を述べている。素人にも分かり易く納得感のあるものはないような気がする。
以下は極限や収束を使わないで説明する一つの方法である（但し、セノンのパラドックスの反駁になっている訳でない）。
＜アキレスが亀に追いつけることの一つの説明＞
簡単のため距離はメートル単位、速度は秒速単位として、動き始める時点の位置を以下のようにする。

アキレスと亀の競争の前提

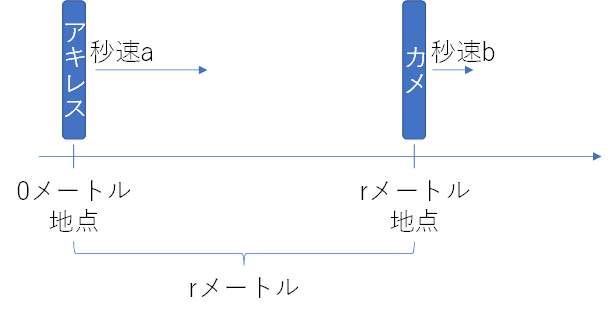
「アキレスは何秒後に亀に追いつけますか？」という問題にすれば、答えは
r/(a-b)秒後と小学生でも解ける。

4．ピュタゴラスの定理は発見にあらず
直角三角形において、直角を挟む2辺をa、bとし、斜辺をcとすると

三平方の定理

が成り立つのは多分、誰でも知っていると思う。「ピュタゴラスの定理」という言い方ともある、というよりこちらが一般的だろう。この定理が成立つことはピュタゴラスに先行する時代の各古代文明で知られていたようだ。「証明」が記録として残っているものとしては（現時点で）一番古いということでピュタゴラスの名を冠している。彼は「ピュタゴラス派」と呼ばれる宗教集団／秘密結社に類するものを率いていたので、本人が証明したかどうかは実際は不明である。

彼は全ての数は有理数(整数を含む)、つまり全ての数はn/m(m、nは整数）で表せると考えていた。しかし三平方の定理でaとｂが1ならｃ=√2（無理数）となる。このように有理数でないものがあることを発見した弟子は処刑されたという逸話がある。前出の音階もそうであるよう、ピュタゴラスは宇宙を含め「万物は数である」を標榜していた。残念乍ら彼のいう数は有理数のみであったということなる。

ところでピュタゴラス教団は、ピュタゴラスの宗教的・哲学的な面に重点を置く派＝アクスマティコイ（聴聞派）と、数学的・科学的な面に重点を置く派＝マティマティコイ（学究派）に分かれていた。後者は数学を表す英語のMathematicsと語源は同じである(ギリシャ語マテーマタは「学ぶべきこと」「学究」という意味）。
＜補足＞
三平方の定理を満たす三つの自然数の組合せ(a,b,c)を「ピュタゴラス数」と呼ぶ。このような組合せは古代メソポタミア文明の考古資料に色々残されている(例：(120,119,169))。ピュタゴラス数は無限に存在する。

【参考：アルキメデスの浮力の原理発見譚】
シラクサの僭主ヒエロン二世から、金細工師が王冠を作るための金を誤魔化していないか、王冠を破壊せず立証せよとの依頼を受けた。入浴中「物体は自身が押しのけた流体の重量と同じだけ浮力を得る」と思いついた。これによって、同じ重さの金塊より王冠の受ける浮力の方が大きければ、王冠に金よりも密度の低い金属が混ぜ込まれていることが立証できる。発見を喜んだアルキメデスは裸のまま浴場を飛び出して「エウレーカ（わかったぞ）！」と叫びながら街を走った。