
電気のおはなしその14・電位とはなにか(その2)
電位の話のつづきです。
話に入る前に、ここまでの話を軽くまとめておきます。
人間が電気を使う理由は、電気から何か役に立つ作用を得るため。
「役に立つ作用」とは、物理学的な「仕事」、つまり「力×距離」である。
例えば、クーロン力に反発して力を加えられて移動させられた電子は、移動させられることによって強力な反発力として仕事を貯め込むことになる。このように貯め込んだ仕事のことを「エネルギー」と呼ぶ。「エネルギーを持っている」とは、「そのエネルギーを放出させることによって他者に仕事を移すことができる」ということ。
クーロン力に反発して力を加えられて移動させられた電子が、移動によって貯め込んだエネルギー差のことを電位差と呼ぶ。
電験3種の国家試験でも、この「電位」の定義式
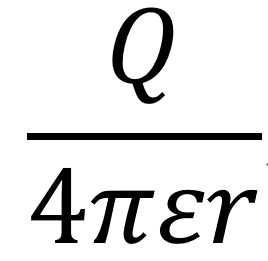
は出てくるのですが、これは「そう定義されている」として暗記事項になっています。電磁気学の勉強を始めた頃は、「rの2乗になっているのが電界、1乗が電位」なんて覚え方をした人も多いかと思います。
実はこれはある意味仕方のないことで、電界の定義から電位を求めるためには積分計算をする必要があるのですが、電験3種の試験レベルは「工業高校卒業程度」のため、微分・積分は試験内容に入っていないんですね。
さて。
それでは、電位を定義するために計算をしてみますよ。
「ある点電荷Q1が存在したとする。そのQ1が作る電界によって、他の点電荷Q2にはクーロン力が働く。このクーロン力によって、Q2に蓄えられるエネルギー(=電位)を定義」します。このとき、Q2が1クーロンとして値を求めておけば、もし5クーロンならその5倍、-3クーロンなら-3倍と楽々計算ができるので、Q2=1クーロンとして電位を求めます。
まず、Q1が距離rの点に作る電界の大きさは、
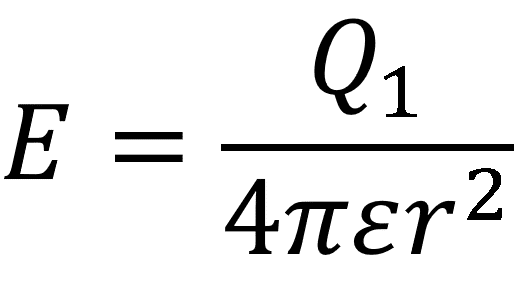
となります。この点に1クーロンの電荷を置いたとき、その電荷に発生するクーロン力は、

で求められます。
以前に少し書きましたが、電荷Q1が作る電界の大きさが真のゼロになる点は、距離rが無限大の地点、つまり宇宙の果てということになります。この点を基準として、
宇宙の果てから、距離rの地点まで、1クーロンの電荷をひたすら運んでくるときの、力×距離の総合計
を計算すれば、これが力×距離すなわち仕事の大きさになるわけですね。
これを実際に求めるためには、宇宙の果てまで行って、そこから1クーロンの電荷をひたすら押してくるという作業が必要になり、事実上無理です。
しかし、数式の上で計算することはできるので、これを求めます。
…とはいえ、1クーロンの電荷に発生するクーロン力は、宇宙の果てでは極めて小さいですが、だんだんとQ1に近づくにつれて大きくなってきます。つまり、クーロン力Fの大きさは、移動に伴って徐々に変化していく値ということになるんですね。
もし、移動中ずっと力の大きさが変わらないのであれば、単純に力×移動距離を計算するだけです。実は、地球の重力の大きさも、厳密にいえば位置によって変化するため単純に求めることはできないのですが、しょせん人間が地球上で数十メールと数百メートル程度移動したところでほとんど無視できるだけの変化しかないため、

ということで、単に力×距離、つまりmghで計算したわけです。
しかし、今回はそう近似することができないため、まともに計算します。
先に式を出してしまうと、
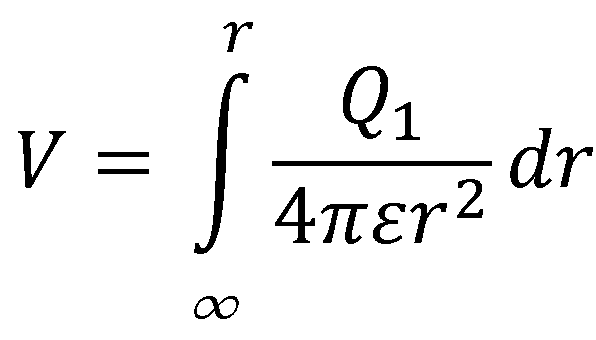
となるんですが、これは、

ということを意味しています。つまり、距離が無限の遠い場所から、距離がrの点まで、rの値をちょーっとずつ変えながらクーロン力の大きさを合計していきますよ、ということになります。
上記の式は、距離rに関係しない部分は外に出すことができるので、

と書き換えることができます。
ここで、積分の計算には、

という基本的な性質があります。実はこれ、「積分は微分の逆計算である」ということと、微分の根本的な原理から導くことができて、その道筋は全然難しくない計算ではあるのですが、今は省略しておきます。
ともかく、式7の原理を利用して式6を展開すると、

となります。[ ]で囲った右上にr、右下に∞が書いてありますが、これは、
カッコ内の式の内容に右上の値を代入したものから、カッコ内の式の内容に右下の値を代入したものを引け
という意味です。これを計算してみます。
見やすくするために変形すると、

ですから

となり、無事「4πεrの1乗、分の1」が出てきました。
めでたしめでたs
(; ・`д・´)ん?
(; ・`д・´)マイナスが付いてるじゃん?
はい、そうなんです。ここまで、仕事の定義、クーロン力の定義、それらを組み合わせて電位まで定義してきましたが、話の流れから言えば電位はプラスの値にならなければおかしいはず。何故なら、クーロン力に逆らって電荷を運んできたわけだから、移動に従ってだんだんと仕事が蓄積されてきたはずだから。
(; ・`д・´)どういうことよ?
って話ですが、実は難しい話ではなく、
Q1クーロンが作る電界は、Q1クーロンから放射状に外に向けて発散していく電気力線として表現されますが、今回はその電界と逆の向きに移動してきたので、そのために正負が反対になった
ということになります。
積分区間を逆にすると、当然結果の正負も逆になります。
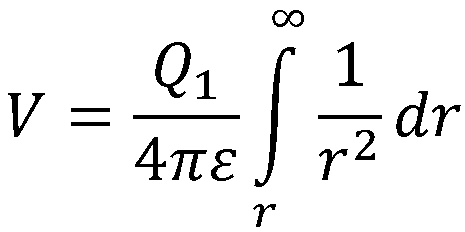
この式は、
「点電荷Q1によって電位という形で仕事を貯め込んでいる、Q1から距離rの地点に存在している1クーロンの電荷を、そのままクーロン力によって移動させて無限遠まで到達した場合、その間に吐き出された仕事の量を求める式」
という意味合いになりますから、当然結果は、
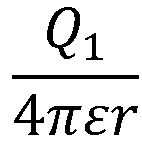
となります。
もう一度確認しますが、物理学的にもっとも素直な考え方で距離rの点の電位を求めたのが式10ですが、これは「Q1クーロンが作る電位が負」を意味しているのではなく、Q1クーロンが作る電界の向きと逆向きに足していったから計算上マイナスの値になっただけで、Q1クーロンが距離rの点に作る電位は式12のとおりプラスの値ということになります。
あ、以上の計算は、すべてQ1が正の値という前提で計算してきましたから、もし負の値であれば電位の値も負になりますので、その点よろしくお願いいたします。
こういう話をするとやっぱり長くなってしまうね。
以上。
