
電気のおはなしその12・スカラーとベクトル、ベクトルの和と差の計算
「ベクトル」と聞いただけで数学アレルギーが~!という向きもいらっしゃるかもしれませんが、電気の勉強をするうえでベクトルの概念を外すことはできませんし、それよりも何よりも、ベクトルって
誰でも日常から当たり前に使っている概念
ですので、ここで簡単に解説しておくことにします。最初はスカラーから。
スカラーは、その大きさだけで決定できる量
のことを指します。
例えば、財布の中に1万円が入っていたとします。1万円は、「右に1万円」とか「上に1万円」とか「下に1万円」なんて概念はありませんよね。俺に1万円くださいという概念はあるあくまでも、「1万円」と言えば1万円でしかありません。
同様にして、「体重64kg」も、上に64kgとか西北西に64kgなんて概念はありませんし、「水1リットル」も、北北西に1リットルとかありません。
このように、その大きさの数値だけで決定できる値をスカラーといいます。
次はベクトル。
ベクトルは、大きさと向きを持った量
のことです。
例えば、「駅から僕の家まで500mだよ」とだけ言われても、駅の何口から出てどの道をどっちに500m行けばいいのか、まで言わないとたどり着くことはできません。この場合、「駅の南口から東南東に500m」のように、距離と向きの両方が分からないと意味がありません。したがって、地図上で地点を表すのはベクトル値です。また、

物体に力を与えて押すときも、図のように右から左に押せば物体は左の方に動きますが、

反対側から押せば、物体は右の方に動きます。したがって、力を与えるといっても、どっちからどっちに向けて力を与えるかによって結果が異なってきます。したがって、「力」もベクトルです。
さらに、男女間の愛情

についても、完全に釣り合いが取れていれば平和なのですが、現実世界では

えてしてベクトルに片寄りがある場合もあり、そのままベクトルを大きくしていくと、
となり、やがてストーカーからDVへと発展していくのです。
1万円も、お金だけを見ていればスカラー量ですが、それを「俺の方に寄越せ」と流れを指し示せばそれはベクトル

ベクトルは、矢印で表します。矢印の長さがその大きさ、矢印の向きがベクトルの向きとなります。これは、地図上で地点を表すのと全く同じですから、感覚的にすぐに分かるのではないでしょうか。
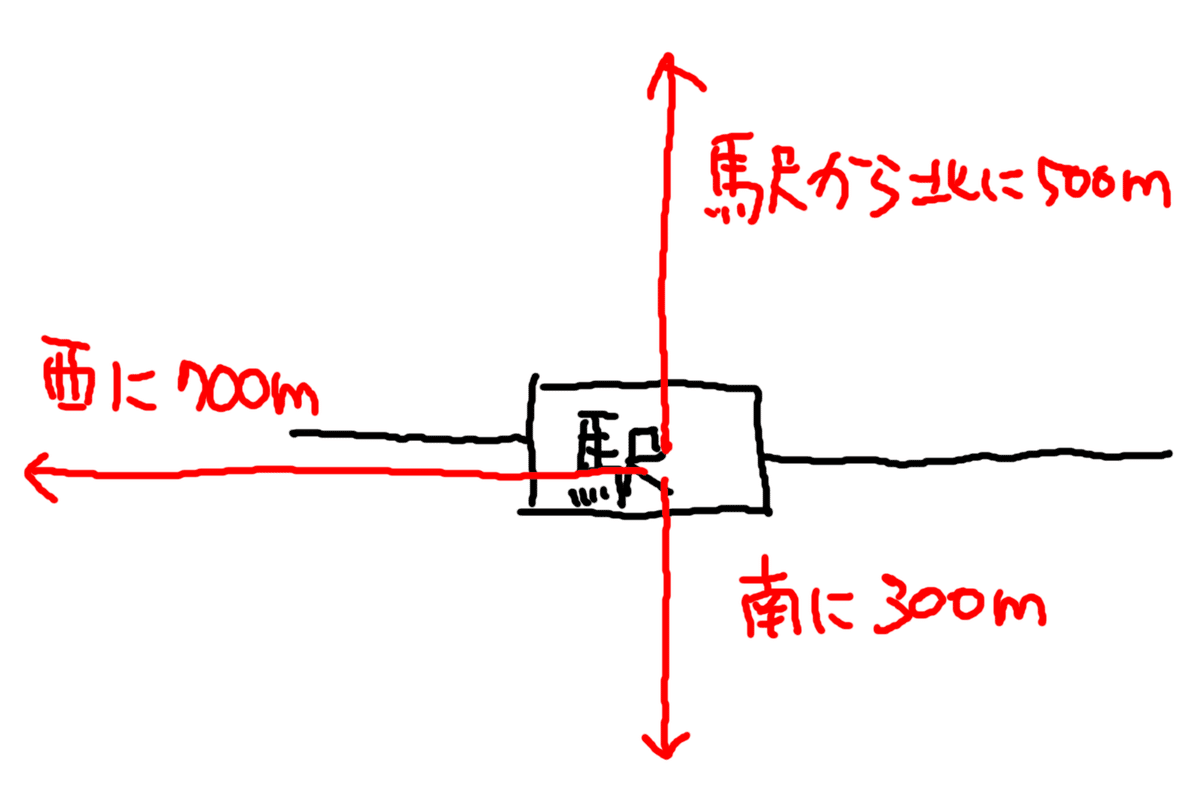
通常の地図では、北を上にするというルールですから、図7のように「駅から北に500m」とか「駅から南に300m」などの位置をベクトルの矢印で表現することができます。
最後に、スカラーとベクトルの和と差について。
スカラーは、単純に足したり引いたりするだけです。例えば、10000円と5000円を足せば15000円、3000円から500円を引けば2500円…のように、なにも難しくはありません。
ベクトルの場合は、大きさだけでなく向きを持っているため、ちょっとだけ難しくなります。
①ベクトルの足し算
ベクトルの足し算は、単純に矢印をつないでいくだけです。そして、最初のベクトルの開始地点と、つないでいった最終地点を結べば、それが答えのベクトルとなります。これも、地図を使えばすぐに分かりますから、図で考えてみることにします。
例えば、駅と自宅の間が図8のような位置関係だったとします。

家に遊びに来る友達に道すじを教えるとき、
駅からこの方角にぴったり500mだから、それをまっすぐ来て。
と伝えてしまうと、野原を突っ切って途中のビルや建物などの壁をぶち破ってまっすぐ進めば確かにたどり着くことはできますが、そんなことをしたら損害賠償がそんなことをする訳にはいかないですよね。
ではどう伝えればよいかというと、
駅から東に400m歩いて、そこから南に300m歩けば着くよ。
とすれば、友達はまず駅から東に400mのベクトルを歩き、次いで南に300mのベクトルを歩いて無事たどり着くことができます。

つまり、
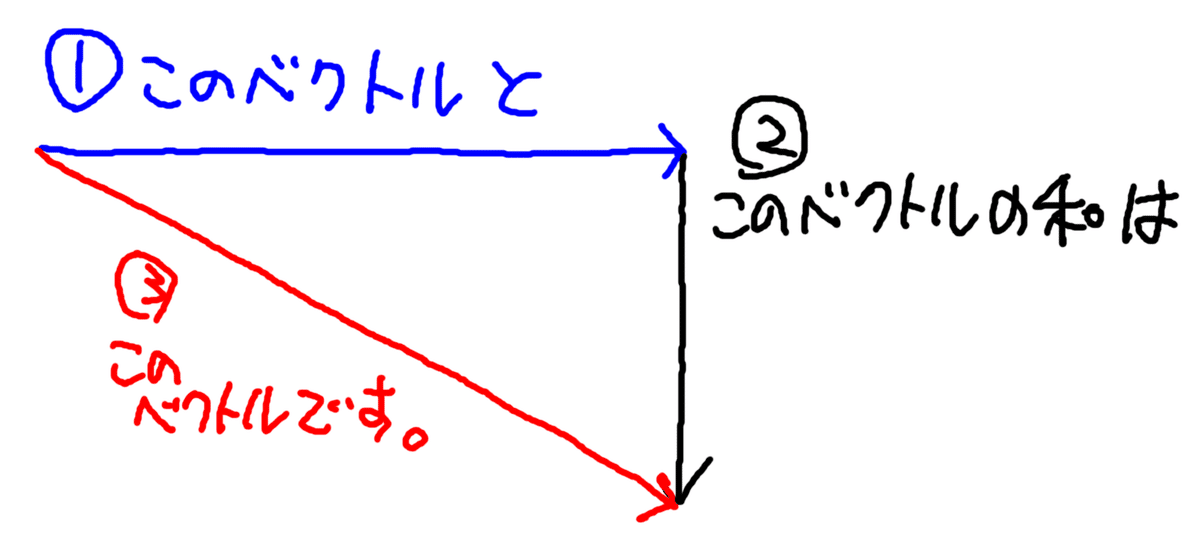
ということになります。
ところで、「東に400m」と「南に300m」の順序を入れ替えたらどうでしょうか。この場合も、

正しくたどり着くことができます。つまり、

ということです。このように、ベクトルの和は、どちらを先に足しても構わないことが分かります。
もちろん、クネクネ道を通る場合のように「東に100m」「南に200m」「東に300m」「南に100m」と刻んだとしても、和の合計のつじつまさえ合っていれば、必ず同じ終端地点にたどり着くことができます。
➁ベクトルの引き算
このような「大きさと向き」を持ったベクトルどうしを「引く」というのはちょっと意味が分からないと思います。結論から言うと、
引かれる方のベクトルの向きを逆にして足す
というのが、ベクトルの引き算になります。でも、ちょっと分かりにくいと思うので、これも駅と家の例で示します。
「駅から家まで、南に300m・東に400m」というところを、「駅から家まで、南に300m行って、そこから西に400mを引いて」と伝えたとします。つまり、南向きのベクトルから西向きのベクトルを引く、という計算です。
こう言われた場合、まず駅から出て南に300mまで行きます。

交差点まで来たら、「西に」と言われたので西を向きます。

そして、そこから「400m引け」と言われているわけですから、友達は後ろ歩きで400m歩けばいいわけです。(前を向いて歩いたら、西向きに足すことになってしまうので)
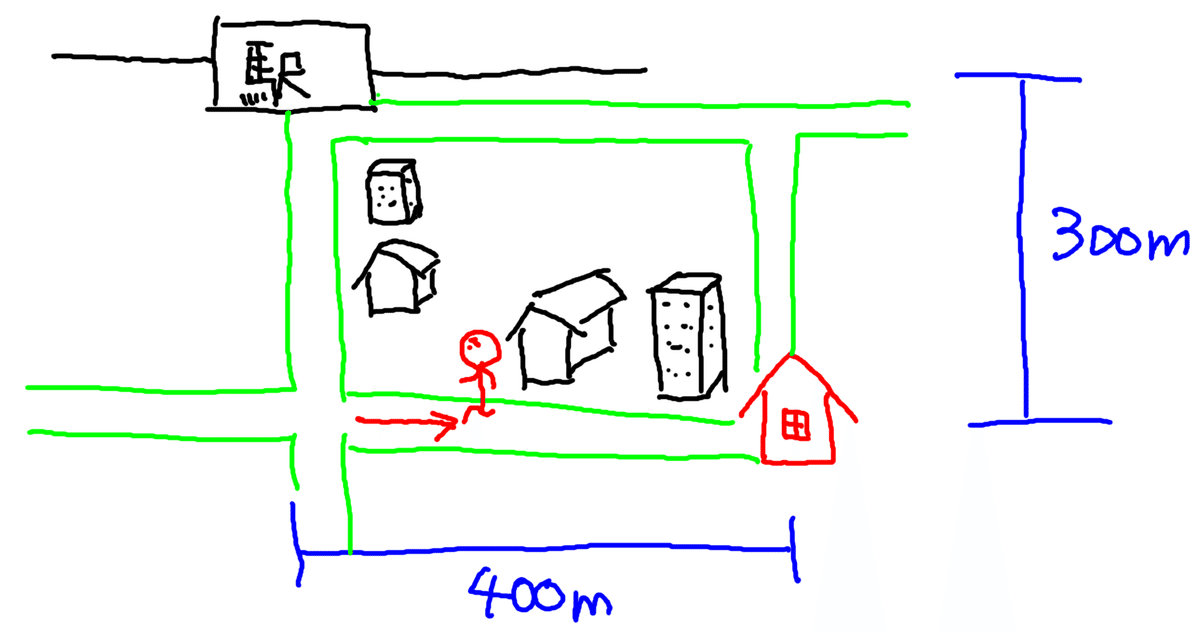
そうすれば、正しく家にたどり着くことができるわけです。
これはまぎれもなく、「西にー400m」と「東に400m」は同じ意味であることを示しています。
他の例でいえば、車を運転していて目的地を通り過ぎてしまったとき、気が付いた地点で車を止めて延々バックすれば目的地に戻りますが、普通はUターンして車の向きを180°逆にし、そこから行き過ぎた分だけ戻りますよね。これも、行き過ぎた距離の分だけベクトルを引き算していることになります。麻雀でも、例えばロン宣言をするときに上家か下家か、あるいは対面かに向かってロン宣言するわけですから、ある意味ロンする相手、という向きを持ったベクトルと言えるかもしれません
さて、ここではスカラーとベクトルの和と差の計算だけを取り上げました。このほかに、掛け算(積)などもあるのですが、ベクトルどうしの積の計算は、「向きと大きさ」の二つの要素を持っている以上、一筋縄ではいきません。細かい話をすると内積と外積というのがあり、内積は高校の数学でも出てくるものの、外積は大学にならないと出てこないちょっと難しい話になってしまいます。また、現段階では「電気の基礎のおはなし」という性質上、その辺の計算は省略して、もしかしてこの先必要となれば、その時に改めて解説しようかと思っています。
数学は数学だけ、別項にまとめた方が良い気もしているんですけどね。…それはそれで大量に書くべきことが発生してしまうという。
長くなりました。この辺で、サヨナラ・サヨナラ・サヨナラ!(淀川長治先生も亡くなってだいぶ経つんだねぇ)
以上。
あ。書き終わってから気づいた補足。
力や電界など、その値が向きを持っているベクトルであるものを表すときは、記号FやEなどを太字のFとかEで書いたり、その記号の上に矢印を書いたりして「この値はベクトルですよ」ということを示したりします。
…そういうルールになってますが、「力とか電界がベクトルなんてのは、当たり前に知ってるっしょ?」という暗黙の了解をもとに、別に太字とか矢印とかを書かないで表現することもあります。
