
税務データのパネル構造を用いた給与収入変化の把握:行政データと実証経済学⑥
経済セミナー編集部noteでは、『経済セミナー』2022年6・7月号から23年10・11月号まで8回にわたって連載した「行政データと実証経済学:東京大学CREPE自治体税務データ活用プロジェクトの実践」を、第1回から改めて掲載していきます。
第1回から第8回までの各回は、以下の noteマガジン に順次公開していきますので、ぜひご覧ください。
このnoteでは、2023年8・9月号に掲載された連載 第 6 回 をお送りします。
著者紹介(執筆当時)
亀山裕貴
東京大学政策評価研究教育センター(CREPE)リサーチアシスタント。
プロフィール
2023年、東京大学公共政策大学院修士号取得。
川口大司
東京大学公共政策大学院教授/大学院経済学研究科教授
プロフィール
2002年、ミシガン州立大学Ph.D.(経済学)取得。2017年10月より東京大学政策評価研究教育センター(CREPE)副センター長、2019年4月から2022年3月まで同センター長を兼任。主著:『労働経済学』有斐閣、2017年。『日本の労働市場』(編者)、有斐閣、2017年。『計量経済学』(西山慶彦・新谷元嗣・奥井亮と共著)有斐閣、2019年。
1. はじめに
これまで、本連載では東京大学政策評価研究教育センター(CREPE)が実施する「EBPM推進のための自治体税務データ活用プロジェクト」のねらいや取り組み、自治体税務データを活用した研究の可能性について紹介してきた。第6回となる今回は、同プロジェクトの目的の1つである「日本の行政におけるエビデンスに基づく政策形成(Evidence-Based Policy Making:EBPM)の推進」を念頭に、市町村の税務データを用いた給与収入の推移を把握する。また、分析の過程で判明した洞察や知見についても、あわせて紹介する [1]。
[1] なお、本稿の実証分析の結果のより詳細な情報は、経済セミナー編集部のサイトにアップしたウェブ付録で公開している。以下では本稿とウェブ付録の対応にも適宜言及しているので、ぜひ参照してほしい。

労働市場の情勢を把握するための賃金指標は、地方行政や中央行政の政策現場で、頻繁に利用されてきた。その最たる例が、金融政策運営だ。 2013年1月、政府と日本銀行は長らく続いたデフレ脱却と持続的な経済成長の実現を掲げ、消費者物価の前年比上昇率2%という「物価安定の目標」を設定した。それ以来、異次元とも言われる金融緩和が実施されてきたが、物価目標の持続的・安定的な達成には依然として至っていないとの見方が支配的だ。この最大の理由として指摘されているのが、賃金の伸び悩みだ。この例が示す通り、賃金指標は政策現場において極めて重要な役割を果たしている。本稿の関心対象である給与収入の推移も、労働市場の足元の情勢を捉える賃金指標の1つとなりうる。
とはいえ、賃金指標の解釈には注意を要する。その1つが、「集計バイアス(aggregation bias)」、または「構成バイアス(composition bias)」と呼ばれる問題だ。集計バイアスとは、労働者構成が変化することで、賃金指標が特定の方向に引っ張られる現象を指す。たとえば、不況期に賃金の低い労働者に集中して失業が発生すれば、個々人の賃金が減少傾向でも、平均賃金指標は上昇しうる。反対に、好況期に賃金の低い個人の労働参加が進めば、個々人の賃金が増加傾向でも、平均賃金指標は低下しうる。つまり、平均賃金と景気循環の関 係を見ると、賃金と景気の関係は逆方向(countercyclical)にバイアスがかかってしまう。これが集計バイアスと呼ばれるもので、こうした賃金指標の問題点は先行研究(たとえば、Bils 1985;Solon et al. 1994)でも指摘されてきた。
足元の日本に目を向けると、昨今、女性や高齢者の労働参加が進むとともに、非正規雇用労働者が増加している(Kawaguchi et al. 2021)。さらに、コロナ禍の収入や就業に対する影響は、特定の産業や非正規雇用労働者、低所得者層をはじめとした特定のグループに集中したと指摘されている(Kikuchi et al. 2020, 2021;Kotera and Schmittmann 2022;Fukai et al. 2021)。そのため、労働者構成に変化があったと考えるのが自然だ。こうした労働者構成の変化は、賃金指標に集計バイアスの影響を与えるおそれがある。そのため、賃金指標を活用する際には、背景にある労働者構成の変化に注意を傾ける必要がある。
労働者構成の変化を考慮に入れた賃金動向を把握するためには、主に2つのアプローチが考えられる。第1に、観測可能な労働者の特徴(属性)を固定することによってサンプルを調整して、平均賃金の変化を推定する手法が挙げられる。その最たる例が、労働政策研究・研修機構が公表するラスパイレス賃金指数だ。同指数は、クロスセクションデータを用いて性別や学歴、勤続年数、従事する産業などの属性を固定することで、これらの構成変化を制御した平均賃金の変化を推定している。これは、物価水準の変化を捉える際に消費のバスケットを固定するという作業に近いと言える。ただし、こうした賃金指標では労働者の観測可能な属性を制御することができるが、観測不可能な異質性を制御することはできないという課題が残る。
第2に、同一労働者の賃金変化をベースとした平均的な賃金変化を測定するアプローチが挙げられる。本稿ではこの手法を採用するが、1つ目のアプローチと比較すると、時間を通じて不変な観測されない異質性も制御できる点で優れている。その反面、同一の個人を時間を通じて追跡できるパネルデータが必要となるため、データの要求水準が高いのが難点だ。実際、既存の賃金関連の政府統計は基本的にはパネル調査となっていない、またはパネル調査となっていたとしても調査単位が事業所であるといった理由から、こうした分析にはそぐわない。その点、同一個人の収入情報を記録した業務データや家計調査などで収集された個票データの方が、こうした分析に適している [2]。
[2] 個票データを用いる場合、慶應義塾大学パネルデータ設計・解析センターの実施する「日本家計パネル調査」や、リクルートワークス研究所の実施する「全国就業実態パネル調査」など、民間のパネル調査も選択肢となりうる。しかし、これら調査はサンプルサイズの点で課題を抱えている。総務省統計局が毎月実施する「労働力調査」もパネル構造を持っているが、世帯員の収入を一度しか聞いていないため、収入はパネル構造にはなっていない。加えて、収入項目の設問は、所定の区分からの選択式となっているため、正確な収入の数値を把握できない。
2. 分析に用いるデータとサンプル
2.1 サンプルの構成
分析には、CREPEが実施する「EBPM推進のための自治体税務データ活用プロジェクト」へ参加した2つの市町村、A市とB市の税務情報を用いる。A市は人口100万人規模の大都市で、B市は人口1.5万人規模の地方の小都市である。このデータは、個人住民税に関する税務の遂行を目的として各自治体が集計したもので、CREPEに対しては研究利用用途で提供されたものだ。各データには、自治体内において個人を一意に識別するために付番された宛名番号、性別、生年、各年度の給与収入などの情報が含まれている。A市のデータは、2016年度から2021年度に課税申告のあった個人全員から50%ランダムサンプリングによって抽出されたもので、毎年、トップ1%の給与収入にはトップコーディングが適用されている [3]。住民税は前年の所得に賦課されるため、データには 2015年から2020年の給与収入が含まれていることとなる。一方、B市のデータは2012年度から2021 年度の間に住民基本台帳に登録のあるすべての個人を対象としており、トップコーディングは施されていない。つまり、2011年から2020年の給与収入の情報がそのまま含まれている。以降では、混乱を避けるため、「年」や「年度」という言葉を用いる際は、住民税の賦課年度ではなく、給与収入のある年を指す。
[3] トップコードされたデータには、元の数値の代わりに各年でトップコードされた給与収入の平均値が挿入されている。今回、トップコードされた値であってもそのまま使用した分析結果を報告するが、これらのデータを除外した分析結果も本稿のウェブ付録で報告する。ただし、2つの分析結果の間に大きな差は確認されなかった。
ここからは、サンプル構成プロセスを説明する。元のデータにおけるA市のレコードは220万5498 件、B市のレコードは19万4818件ある。このレコードから、まず生年や性別が欠損しているレコードを落とした。この操作で、A市のレコードは28 件、B市のレコードは14件落とされた。かつ、B 市に関しては当該年度中に死亡した個人を判別できるため、追加で2440件を落とした。
次に、分析対象を25歳以上60歳未満の個人に絞ることとした。25歳未満の個人は就学中の可能性が高いうえ、両市の税務データには個人の学歴や教育年数といった変数が存在しないため、給与収入の変動から就学や就業による影響を除去できない。同様に、60歳以上の個人は退職や再雇用、再就職などの選択により、給与収入に変動が生じてしまう。そのため、25歳未満および60歳以上の個人はサンプルから除外した。この操作の結果、A市のレコードは104万7109 件(元データの約47.5%)、B市のレコードは6万8022件(元データの約34.9%)となった。
また、極端に低収入な個人の収入変動が分析結果に影響を与えるのを避けるため、労働市場へ十分に定着していないと考えられるオブザベーションをサンプルから除外した。この点に関しては、 GRID(Global Repository of Income Dynamics)の実践を参考にした。GRIDは、ミネソタ大学ミネソタ・エコノミクス・ビッグデータ研究所、プリンストン大学、スタンフォード大学による共同イニシアチブであり、現在、13カ国の所得格差に関する統計をオープンアクセスで提供している [4]。そして、GRIDがサンプルを絞り込むために用いている1つの基準が、「労働市場への意味あるアタ ッ チ メ ン ト(meaningful attachment to the labor market)」という閾値(以下「MA閾値」)だ。この閾値は最低賃金で週20時間、四半期働いたときに得られる収入として定義されており、所得不平等などを分析するうえで使用するログベースの統計量に歪みが生じることを避けるため、同閾値以下の極端に収入の低い個人はサンプルから除外されている(Guvenen et al. 2022, p.1330)。本稿では、極端に低収入のオブザベーションは、労働市場の平均的な収入変化を捕捉するうえで障害となると考え、MA閾値以下の年間給与収入を持つオブザベーションをサンプルから除外した。たとえば、ある個人の $${t}$$ 年の給与収入の値がMA 閾値より低い場合、$${t}$$年のオブザベーションは削除されるが、$${t-1}$$ 年や $${t+1}$$ 年の給与収入がMA閾値より高ければ、これらのオブザベーションは削除されない。ただし、この操作が適用されたことで、分析サンプルは母集団における低収入層を代表していない点には注意が必要だ。以上の結果、A市のレコードは92万8758件(元データの約 42.1%)、B市のレコードは5万232件(元データの約25.8%)となった [5]。
[4] 興味のある読者は、Guvenen et al.(2022)や同論文が掲載されたQuantitative Economics, Volume 13, Issue 4、およびGRIDの公式ウェブサイトなどから詳細を確認できる。
[5] 各年度、各自治体におけるMA閾値の値は厚生労働省(2021)「平成14年度から令和3年度までの地域別最低賃金改定状況」から算出した。
本分析で自治体税務データを用いる最大の強みは、給与収入を正確に把握できる点にある。また、ある自治体における住民全員を対象とした、大規模なサンプルを確保できる点でも優位性がある。さらに、回答拒否による欠落に伴う非標本誤差の懸念が小さいことも、既存のサーベイデータと比較した優位点と言える。
他方、われわれのデータの弱みは、分析に活用できる変数が少ないことにある。たとえば、税務に直接的に関係のない労働日数や労働時間などの情報は収集されていない。そのため、収入変動の要因を時間当たり賃金と労働時間の変化に分離するといった分析を行うことができない。また、性別や年齢、続柄といった基本的な情報を除き、人口統計的な情報も限られており、学歴や職種などの情報もわからない。第3節の実証戦略で述べる通り、本稿で用いるモデルは個人の観測されない異質性を制御するため分析自体に支障はないが、異質性を詳細に検討することができない点で課題が残る。また、サンプルからの脱落によって生じる問題への懸念もある。個人が死亡したり、自治体から転出した場合、サンプルからは脱落が生じる。仮に、脱落が給与収入に影響を与える要因と相関している場合、推定結果にバイアスが生じる可能性がある。しかし、後述の通り、今回の分析では個人固定効果を含めた分析を行うことから、個人固定効果で説明できる範囲の脱落傾向に関するバイアスは軽減できていると考えられる。最後に、今回利用するデータは2つの自治体に限られることから、本稿の分析結果が他の自治体についても一般的に適応できるかどうかは不確かであることも指摘しておく。
2.2 記述統計
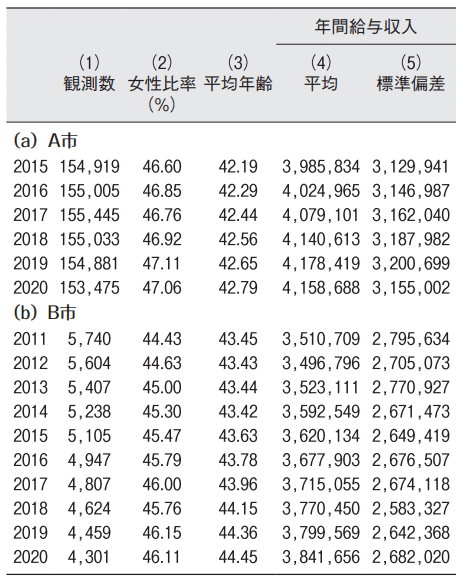
分析に用いるサンプルの基本的な特徴は表1にまとめた [6]。まず、列 (1) には観測数を記載した。A市のサンプルは2015年から2020年までをカバーし、毎年15万人以上の給与収入者の情報が含まれている。一方、B市のサンプルは2011年から2020 年までをカバーし、4300~5700人程度の情報が含まれているが、少子高齢化による影響で、観測数が著しく減少している。続く列 (2) と列 (3) には、女性比率と平均年齢を表した。ここからわかる通り、両自治体において女性比率および労働者の平均年齢は増加傾向にある。特に、B市では、2011 年から2020年の間で、女性全体の構成比率は約 1.7%ポイントも上昇している。列 (4) と列 (5)には、給与収入の平均値と標準偏差を示している。ここから、両市において給与収入の平均値は年々増加傾向にあることが読み取れる。
[6] A市の年間給与収入に対して適用されたトップコーディングの割合、閾値、平均値については、ウェブ付録の表A1に示した。
次に、給与収入の分布を見ていこう。図1に年間給与収入のヒストグラムを自然対数軸上に示した。階級の幅は0.05とした。まず、両自治体において男性の方が女性よりも収入分布が高い傾向が見て取れる。特に女性については、住民税や所得税が非課税となる100万円前後で出っ張りが見られることから、就労調整を行っていると推測される。このことから、税制を受けて内生的に労働供給を調整している労働者の実態が想像される。以下の分析では、個人の就労調整行動を所与として収入の推移を推定していくが、本プロジェクトにおいては税・社会保険制度と就労調整の関係自体を1つの研究課題として捉えていることも述べておく [7]。同トピックに関する概論は、本連載第4 回(近藤 2023)を参照してほしい。また、A市のヒストグラムでは給与収入の値がある閾値を超えたところで度数が0となり、それより右に再び出っ張りが見られる。これは、トップコーディングによって生じたものだ。
[7]「EBPM推進のための自治体税務データ活用プロジェクト」の詳細は、本学術研究領域と連携して運営されている研究プロジェクト「税務データを中心とする自治体業務データの学術利用基盤整備と経済分析への活用」のウェブサイトを参照。


最後に、性別と年代層のクロスセクションに着目して、労働者構成の変化を確かめる。図2は、特定の性別、年代層の労働者が各年の労働者全体に占める構成比率を示したものだ。まず、A市に目を向けると、2015年から2020年にかけて男女ともに50代の労働者の構成比率が1%ポイント前後増加していることがわかる。その反面、30代の労働者の構成比率は1%ポイント強減少している。そして、それ以外のグループについては、さほど変化が見られない。B市については、A市よりも観測期間が長いことも重なってか、より大きな変化が見られる。女性労働者の方では、2011年から 2020年の期間で、40代と50代の構成比率は上昇しているが、20代と30代の構成比率は減少している。もう一方の男性労働者では、40代の構成比率は約 4%ポイントも増加したが、他の年代の構成比率は減少していることが読み取れる。


上記のような労働者構成の変化が起こることで、賃金指標にはどのような影響があるのだろうか。たとえば、女性が比較的低収入のパートタイム労働に従事し、就労調整を行う傾向があれば、女性の労働参加が進むことで、労働者全体の平均収入が低下するおそれがある。また、勤続年数が長い労働者の方が高い賃金を得る傾向があるとすれば、労働者の高齢化が進むことで、平均収入は上昇する可能性もある。ただし、水面下では性別や年齢層以外の構成変化も起きている可能性がある。そのため、第1節で述べた通り、個々の労働者の観測可能な属性に加えて、観測できない異質性を制御した収入変化を捉える必要がある。
3. 実証戦略
最も単純なモデルとして、自然対数変換した個人 $${i}$$ の $${t}$$ 年における年間給与収入$${\ln Earning_{i t}}$$ を被説明変数、年度ダミー$${YearDummy _t}$$ を説明変数とするモデルを考える。関心対象である年度ダミーの係数 ×Ʊ は、最小二乗法によって求められ、データに含まれる最も過去の年度と比較した $${t}$$ 年の給与収入の変化分を表す。ただし、ここでは $${\beta_{t}}$$ は個人間で一定であると仮定している。
$$
\ln Earning_{i t}=\beta_0+\sum_{t} \beta_t YearDummy _t+u_{i t} \qquad (1)
$$
モデル (1) の欠点は、労働者全体が高齢化したときに、加齢による増収が年度の影響として捉えられてしまう点だ。この問題を解消するため、年齢$${Age_{it}}$$を説明変数に加えたモデルを考える。今回用いるデータには労働市場での経験年数や潜在経験年数を計算するのに必要な学歴が含まれていないため、代替的に年齢を統制することで賃金プロファイルをはじめとした影響の制御を試みる。ただし、年齢$${Age_{it}}$$は年度ダミー$${YearDummy _t}$$に加え、この後モデルで制御することとなる生まれ年(個人固定効果に含まれる)にも依存するため、完全な多重共線性が発生する。この識別上の問題を避けるために、5歳の区分ごとに標準正規分布の確率密度関数 ñ で$${Age_{it}}$$を変換することで[8]、 $${\beta_{x} \phi(・)}$$をもって非線形の賃金プロファイルを仮定する。
[8] 正確には、Card et al.(2018)の議論に従い、年齢をガウス基底関数によって変換することとした。
$$
\begin{aligned}
\ln Earning_{i t}= & \beta_0+\sum_t \beta_t YearDummy _t \
& +\sum_{x \in 25, \ldots, 55} \beta_x \phi\left(\frac{A g e{i t}-x}{5}\right)+u_{i t}\qquad (2)
\end{aligned}
$$
最後に、個人固定効果 $${\alpha_i}$$ を含めたモデルを考える。これにより、個人に特有の時間に依存しない、コホートや性別、教育年数、潜在能力などの異質性を制御する。このとき、固定効果モデルを用いて $${\beta_t}$$ を推定することで、個々人の異質性を制御した平均的な賃金変化を捉えることができるのではないかというのが、ここでのアイデアだ。
$$
\begin{aligned}
\ln Earning _{i t}= & \sum_t \beta_t YearDummy_t \
& +\sum_{x \in 25, \ldots, 55} \beta_x \phi\left(\frac{\text { Age }{i t}-x}{5}\right)+\alpha_i+u_{i t} \qquad(3)
\end{aligned}
$$
以上のモデルでは、$${\beta_{t}}$$ や $${\beta_{x}}$$ が労働者間で一定であると仮定している。しかし本来、従事する産業や職業、企業規模に加え、教育年数やコホートをはじめとする個人の属性に応じて、収入変動や賃金プロファイルが異なると仮定した方が現実に即している。そこで、以下では具体例として男女別のサブサンプル分析も実施することとする。
4. 分析結果
4.1 メインサンプル分析
4.1.1 A市
A市の分析結果は、図3の通りとなった。同図は横軸に年度、縦軸に2015年比の年間給与収入成長率をパーセンテージでとり、モデル (3) の分析結果のみ濃い線で表した。推定値の周りにあるバンド(縦方向の線)は95%信頼区間を示しているが、その計算にあたっては、同一個人の誤差の相関を考慮して、クラスターロバスト標準誤差を使用した [9]。
[9] なお、メインサンプル分析で推定された係数などの詳細は、ウェブ付録の表A2に示した。また、トップコードされたデータを除外した分析結果は、表A3に示した。

まず、年度のみを説明変数とするモデル(1)と、これに年齢を加えたモデル (2) を比較する。この 2つのモデルで推定された成長率の値の間には、95%信頼区間において統計的に有意な差はないが、モデル (2) の方がモデル (1) よりも成長率を小さく見積もっていることがわかる。このとき、推定された年齢の係数 $${\hat{\beta_{x}}}$$ は負の値をとることから、$${ \phi(・)}$$ と $${YearDummy_t}$$ の間には負の相関関係が成り立っている。やや解釈 が難しいが、年齢、 $${Age_{it}}$$ は5歳区分で分割されており、年齢はこの区分ごとに標準正規分布の確率密度関数、$${ \phi}$$ によって変形されて、単調減少の正の値をとる。そのため、$${ \phi(\cdot)}$$ と $${YearDummy_t}$$ の間に負の相関関係があることは、年齢と年度の間に正の相関関係があることと整合的だ。この示唆は、A市の労働者の平均年齢水準が上昇している事実と符合する。
次に、年度と年齢を説明変数とするモデル (2) と、これに個人固定効果を加えて個人の異質性を制御したモデル (3) を比較する。すると、モデル (3) の方がモデル (2) よりも給与収入成長率を大きく見積もっていることがわかる。よって、A市の場合は、個人固定効果を導入して個人の異質性を制御しなければ、給与収入成長率に下方バイアスがかかりうるという示唆が得られた。
モデル (3) で推定された個人固定効果の要約統計は、表2に示している。これを見ると、推定された個人固定効果の平均値や中央値、第3四分位数にはおおむね減少傾向があることが確認できる [10]。よって、全体としては、観測されない異質性によって収入の低いタイプの個人が労働市場で増えてきていると推測される。個人固定効果には、性別やコホート、教育年数、潜在能力をはじめとするさまざまな要因が含まれていることから、この背景にある具体的な要因は特定できない。しかし、2.2項で例示した通り、労働者構成における女性比率の増加は要因の1つとして有力かもしれない。なぜなら、平均的に女性労働者の方が給与収入の低いタイプの個人が多ければ、女性の労働者構成比率が上昇することで年度と個人固定効果に負の相関関係が生じるためである。
[10] 年度の項と個人固定効果の相関係数はウェブ付録の表A2に示したが、$${-0.010}$$となっており、弱いながらも負の相関が認められる。

4.1.2 B市
B市の分析結果は、図4の通りとなった。B市の場合、2011年度からデータが存在するため、同図の縦軸には2011年比の年間給与収入成長率をパーセンテージで示した。

まず、年度のみを説明変数とするモデル (1) と、これに年齢を加えたモデル (2) を見比べる。この 2つのモデルで推定された年度の係数の間に統計的に有意な差はないが、モデル (2) の方がモデル (1) よりも給与収入成長率を若干小さく見積もっている。説明が重複するため省略するが、このとき、年度と年齢に正の相関関係が成り立ち、これはサンプルにおける平均年齢水準の上昇と整合的だ。
次に、年度と年齢を説明変数とするモデル (2) と、これに個人固定効果を加えて個人の異質性を制御したモデル (3) を比較する。両者の間でも統計的に有意な差は確認できないが、モデル (3) の方がモデル (2) よりも給与収入成長率をわずかながら小さく見積もっていることがわかる。そして、表3に示したモデル (3) で推定された個人固定効果の要約統計を見ると、第3四分位数のみ減少傾向が確認されるが、それ以外では特筆すべき傾向は見られない。そのため、年度と個人固定効果の間にほとんど相関関係は確認されず、観測不可能な属性による集計バイアスはB市においては無視できることを示している。

4.2 男女別サブサンプル分析
本項では、男女別にサブサンプル分析を実施する。第3節で言及した通り、サブサンプル分析を実施するメリットは、観測可能な要因に応じて異なる給与収入成長率や賃金プロファイルを仮定できることにある。ここでは、性別を例にとって分析を行う。
4.2.1 A市
A市におけるサブサンプル分析の結果は、図5 のようになった。左のパネルが女性サンプル、右のパネルが男性サンプルを用いた2015年比の給与収入成長率の推定値を表している [11]。
[11] 実際に推定された係数などの詳細は、ウェブ付録の表A4に示した。

メインサンプル分析と同じく、モデル (1) とモデル (2) で推定された給与収入成長率の値は、 95%信頼区間において統計的に有意な差は検出されなかったが、男女ともにモデル (2) の方がモデル (1) よりも給与収入成長率を低く見積もる結果となった。先述の通り、これは年度と年齢の間に正の相関関係があることを示唆しており、男性労働者と女性労働者の間で年齢水準が上昇していることと合致する。
興味深いのは、図中の濃い線で示されたモデル (3) の推定結果を薄い線で示した他のモデルと比べたときに、男女間で異なる示唆が得られることだ。まず、左パネルの女性サンプルを対象とした分析結果を見ると、濃い線で示した個人固定効果を入れたモデル (3) の方が、薄い線で示した個人固定効果を入れないモデルよりも、給与収入成長率を高く見積もっている。よって、女性の場合、個人の異質性を考慮しなければ給与収入成長率に下方バイアスがかかる。このとき、表4のパネル (a) からわかる通り、推定された個人固定効果には減少傾向が見られる。そのため、女性労働者については年度と個人固定効果の間には負の相関関係があり、観測されない異質性によって収入の低いタイプの労働者が増加していると考えられる。

他方、右パネルの男性サンプルの分析結果からは、濃い線で示した個人固定効果を入れたモデル (3) の方が、薄い線で示した個人固定効果を入れないモデルよりも、給与収入成長率を低く見積もっている。よって、男性労働者の場合、個人の異質性を考慮しなければ、給与収入成長率に上方バイアスがかかる。表4のパネル (b) を見ると、推定された個人固定効果の平均値や第1四分位数、中央値には上昇傾向、第3四分位数には減少傾向が観測できる。つまり、男性労働者全体としては、観測されない異質性によって収入の高いタイプの個人が増えていると推測される。今回、なぜ男女間で異なる結果が得られたのかは不明だが、A市の場合、性別に応じて給与収入の成長率は異なる方向にバイアスがかかっているようだ。
もう1つ明らかになったのは、すべてのモデルにおいて、女性サンプルの方が男性サンプルと比べて給与収入成長率の推定値が高くなったということだ。この背景には、低収入層の方が給与成長の幅が大きいことが影響していると思われる。前掲の図1 (a) で見た通り、女性労働者の収入分布は男性労働者と比較して低い。これにより、女性サンプルの方が男性サンプルよりも推定された給与収入成長率が大きくなったと考えられる。そして、女性の給与収入成長率が高い結果、メインサンプルの給与収入成長率の推定値も引き上げられていたと推測される。
4.2.2 B市
B市でも男女別にサブサンプル分析を行ったところ、分析結果は図6のようになった[12]。
[12] 実際に推定された係数などの詳細は、ウェブ付録の表A5に示した。

まず、これまでの分析結果と同様、統計的に有意な差は見られないが、男女ともにモデル (2) の方がモデル (1) よりも給与収入成長率を小さく見積もっていることがわかる。次に、濃い線で表した個人固定効果を入れたモデル (3) と他のモデルを比較すると、こちらも統計的に有意な差は検出されなかったが、男女ともにモデル (3) の方が給与収入成長率を低く見積もっていることが見て取れる。このとき、表5からわかる通り、女性サンプルについては2011年から2015年頃にかけて推定された個人固定効果の分布に上昇傾向が見られるが、その後はおおむね減少傾向となっている。よって、2015年までは収入の高いタイプの個人が増加し、その後、収入の低いタイプの個人が増加したと推測される。もう一方の男性サンプルで推定された個人固定効果の平均値、第1四分位数、中央値については若干の上昇傾向が観察されるが、第3四分位数には減少傾向が確認される。最後に、B市の分析結果でもすべてのモデルにおいて、女性の方が男性と比べて推定された給与収入成長率が高くなっていることも指摘しておく。

5. おわりに
本稿では、労働者構成の変化を考慮した収入動向を把握することを目的として、平均的な給与収入の成長率を推定した。分析にはA市とB市の税務データを使用し、時間を通じて不変な個人の異質性を考慮した固定効果モデルでの推定を試みた。メインサンプル分析の結果からは、A市の2015 年から2020年の給与収入成長率は8.37%程度と推定され、年齢と個人の異質性を考慮しなければ、成長率に下方バイアスがかかることがわかった。考えられる一因は、労働市場において、観測されない異質性に由来する収入の低いタイプの個人が増加しているということだ。確定的なことは言えないが、収入が低い女性の労働参加が進んでいるのは全国の都市部において進行している現象であり、A市において得られた結果はほかの都市部においても成立している蓋然性が高い。
一方B市では、2011年から2020年の給与収入の成長率は11.49%程度(2015年比では約8.08%)と推定され、年齢と個人の異質性(個人固定効果)を考慮しなければ、給与収入成長率に上方バイアスが生じる可能性が示された。ただし、年齢や個人の異質性を考慮しない場合と比べても、統計的に有意な差は検出されなかった。A市では観察された集計バイアスの問題が、B市では統計的に有意には観察されなかったことは、一部の地域で得られた結果をもって全国的な現象を推測することの危険性を示唆している。
次に、給与収入成長率の異質性を許容するために、性別に着目してサブサンプル分析を実施した。
まず、A市の女性サンプルの2015年から2020年の給与収入成長率は15.79%程度と推定され、年齢と個人の異質性を制御しなければ、給与収入成長率に下方バイアスが生じることがわかった。一方、男性サンプルでは約2.10%と推定され、反対に上方バイアスが生じることがわかった。加えて、この分析からは、女性労働者については観測されない異質性によって収入の低いタイプの労働者、男性労働者については収入の高いタイプの労働者が増加しているという分析結果も得られた。これは先ほど述べた、女性の労働参加が進むことによって給与収入成長率に下方バイアスが生じるという推論と整合的である。他方、B市の女性サンプルの2011年から2020年の給与収入成長率は約18.28%(2015年比では約 14.04%)、男性サンプルの成長率は約6.33%
(2015年比では約3.45%)と推定され、男女ともに年齢と個人の異質性を制御しなければ給与収入成長率が低く見積もられる傾向があるとわかった。しかし、これらの要因を制御しないモデルの分析結果と比較しても、統計的に有意な差は確認できず、年齢や観測不可能な属性による集計バイアスは無視できると考えられる。
また、両市の分析結果からは、女性サンプルを用いた推定結果の方が男性サンプルの推定結果よりも給与収入成長率が大きくなることが判明した。この背景には、女性の方が男性と比べて収入分布が低く、低収入層の方が給与収入成長率が高いことが影響していると推測される。これは固定効果で吸収される収入のレベルでの異質性だけではなく、収入の成長率の異質性をも考慮することが大切であることを示唆している。
以上の分析結果をふまえると、賃金指標を作成するうえで、労働者の年齢や性別、観測されない異質性などの構成変化を考慮することは、重要な意味があると思われる。その重要性を強調したうえで、留意点として給与収入成長率自体に異質性が存在する可能性があることも指摘しておく。今回、地域や性別という観測可能な属性をとっても、平均的な給与収入成長率は異なることが明らかになったが、前年度の収入や従事する産業や職種、学歴などの個人の属性に応じて、異なる収入成長の傾向に直面するということは、十分考えられる。こうした給与収入成長率の異質性を考慮しなければ、集計バイアスとは異なる形でのバイアスが生じうる。そのため、将来的には地域や性別以外の異質性をふまえたうえで、実証戦略を注意深く検討する余地がある。
最後にデータ整備の重要性も強調しておく。本稿では、同一労働者に着目した収入変化に着目することで、平均的な賃金変化を捉える手法を提案したが、この分析を行うには正確な給与収入を記録したパネルデータが求められる。その点、個人住民税の税務データは最適だが、2.1項でも述べたように利用可能な変数が限られている点では、限界がある。たとえば、個人の学歴や職種、従事する産業、企業の属性などがわかれば、より詳細に異質性の検討ができただろう。また、時間当たり賃金や労働時間がより細かな頻度でわかれば、年間給与収入よりも細かなレベルで速報性を持って賃金変動が推定できるはずだ。変数の問題に加えて、サンプル構成上の問題も存在する。現状、個人住民税の税務データは自治体ごとに異なる管理がなされており、データ収集・データ整備のハードルが極めて高い。そのため、日本全体の代表性を兼ね備えたサンプルを構築するまでには、長い道のりがある。以上をふまえると、現段階では個人住民税の税務データは既存の賃金統計を代替するものとは言えず、両者を補完的に活用するためにも双方のさらなる利用促進や改良が求められる。同時に民間の給与計算システムのデータをはじめとする民間業務データの利活用も視野に入れることが、重要と言えるのではないだろうか。
参考文献
厚生労働省(2021)「平成14年度から令和3年度までの地
域別最低賃金改定状況」。
近藤絢子(2023)「自治体税務データの可能性──ライフサイクルを通じた働き方の選択を探る(行政データと実証経済学、第4回)」『経済セミナー』2023年2・3月号:65-73。
Bils, M. J.(1985)”Real Wages over the Business Cycle: Evidence from Panel Data,”Journal of Political Economy, 93(4): 666-689.
Card, D., Cardoso, A. R., Heining, J. and Kline, P.(2018) “Firms and Labor Market Inequality: Evidence and Some Theory,”Journal of Labor Economics, 36(S1): S13-S70.
Fukai, T., Ichimura, H. and Kawata, K.(2021)”Describing the Impacts of COVID-19 on the Labor Market in Japan until June 2020,”Japanese Economic Review, 72 (3): 439-470.
Guvenen, F., Pistaferri, L. and Violante, G. L.(2022) “Global Trends in Income Inequality and Income Dynamics: New Insights from GRID,”Quantitative Economics, 13(4): 1321-1360.
Kawaguchi, D., Kawata, K. and Toriyabe, T.(2021)”An Assessment of Abenomics from the Labor Market Perspective,”Asian Economic Policy Review, 16(2): 247278.
Kikuchi, S., Kitao, S. and Mikoshiba, M.(2020)”Heterogeneous Vulnerability to the COVID-19 Crisis and Implications for Inequality in Japan,”RIETI Discussion Paper Series, 20-E-039.
Kikuchi, S., Kitao, S. and Mikoshiba, M.(2021)”Who Suffers from the COVID-19 Shocks? Labor Market Heterogeneity and Welfare Consequences in Japan,”Journal of the Japanese and International Economies, 59, 101117.
Kotera, S. and Schmittmann, J. M.(2022)”The Japanese Labor Market During the COVID-19 Pandemic,”IMF Working Paper, No.2022/089
Solon, G., Barsky, R. and Parker, J. A.(1994)”Measuring the Cyclicality of Real Wages: How Important is Composition Bias?”Quarterly Journal of Economics, 109(1): 1-25.
「自治体税務データ活用プロジェクト」の最新情報については、以下の文部科学省科学研究費補助金学術変革領域研究 (B)「税務データを中心とする自治体業務データの学術利用基盤整備と経済分析への活用」のウェブサイトをご覧ください!

*本稿は、『経済セミナー』2023年8・9月号からの転載です。
いいなと思ったら応援しよう!

