
西條辰義「日本人は『いじわる』がお好き?!」
〈著者紹介〉
西條辰義(さいじょう・たつよし)
高知工科大学フューチャー・デザイン研究所 所長
1952年生まれ。1985年、ミネソタ大学経済学部Ph.D.取得。
詳細は【こちら】もご覧ください。
本投稿は『経済セミナー』2005年12月号からの転載です。
はじめに
友達と2人で一緒にアルバイトをするとしましょう。あなたに決定権がある場合、あなたは次の どちらの店を選びますか。①あなたも相手も時給1500円、②あなたは1400円で相手は1200円。①を選ぶのが当たり前でしょうか。
本稿では、公共財供給実験を出発点とし、20世紀型の経済学の問題点を振り返りつつ、ニューロサイエンスを含む生物学などの分野と21世紀型の 社会科学がどのように関連するのか眺めてみましょう。
公共財供給と囚人のディレンマ
あなたと相手がお互いに10ドルずつ持っているとしましょう。この10ドルから幾らかお金を出し合うと、〈出したお金の合計額×0.7〉分のお金を互いに受け取れるという状況を考えてみましょう。話を簡単にするために、お互いに出せるお金は0ドルか10ドルに限ります。そうすると、表1の右下のセルのように、2人が共に10ドル出せば、合計額は20ドルなので、お互いに14ドル(=20×0.7)のお金を受け取れます。もちろん、2人とも出さなければ、左上のセルのように、手元に10ドルが残ります。相手が出して、あなたが出さなければ、あなたの場合、17ドル(=相手の出した10ドル×0.7+手元の10ドル)もらえることになります。相手は手元に残るお金がないので7ドルしかもらえないのです。
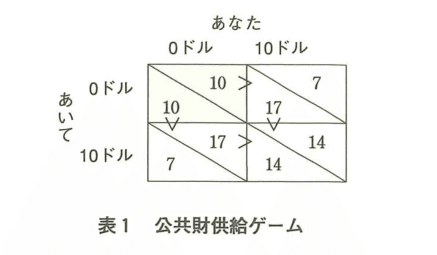
相手が出さないとするなら、あなたが出さないならあなたの利得は10ドル、出すなら7ドルなので、出さないほうがよいのです。相手が出すとしても、あなたが出さないなら17ドル、出すなら14ドルなので、やはり出さないほうがよいことになります。どっちにしても出さないほうがよいのです。2人ともそう考えるなら、結局のところ、2人とも出せばお互いに14ドルもらえるのにもかかわらず、2人とも出さずにもとの10ドルのままになります。
このゲームは囚人のディレンマとよばれています。ここでは公共財供給の文脈で考えてみましょう。お互いにお金を出しあって公共財(たとえば 金額の大きさに応じて長くなる道路)を作るのですが、それはみんなで使うことができるので、あなたも相手も道路を使うことによって得をするのです。この例だと、一人だけで道路をつくると損をしてしまうものの、2人でつくると互いに得をする、という設定になっています。
1988年の頃です。カルフォルニア大学サンタバーバラ校の図書館でアイザック・ウォーカー(Quarterly Journal of Economics, 1988)の公共財供給に関する実験論文を眺めていました。表1のゲームで、自由に0と10ドルの間で、出すお金を選べるとしましょう。そうすると、被験者は結構お金を出すのです。同じ実験を10回繰り返すのですが、1回目あたりは約半分、最終回でも2~3割出すというのです。表1の場合、相手がどのような戦略をとっても、自分にとってはベストな戦略があるという特徴があります。このような戦略を支配戦略とよびます。その頃は、天真爛漫に、被験者が支配戦略をとらないなんておかしい、と思ったものです。
そこで、公共経済学の授業で、アイザック・ウォーカーたちの実験とほぼ同じものをやってみました。結果は彼らとほぼ同じになるのです。実験研究では被験者に謝金を払わねばならない、という話を聞き、給料から500ドルほどさいて、謝金を支払う実験をしたのもこのころです。やがて、 囚人のディレンマのゲームには膨大な実験があり、被験者がなぜ支配戦略をとらないのかが大きなトピックになっているのを知りました。
公共財供給実験の論文を読み進むにつれて、社会学研究者と経済学研究者の間で、結構な「せめぎあい」があるのがわかりました。社会学者のマーウェルたちは、1970年代後半頃から公共財供給実験を実施し、手持ちのお金のうち4割から6割を出すのが普通で、フリーライドする被験者はまれだ、と結論づけたのです。さらにマーウエル・エイムズは、「フリーライドをするのは経済学研究者だけ?」(1981年)という挑発的なタイトルの論文を『Journal of Public Economics』という専門誌に発表しました。ウィスコンシン大学の経済学専攻の院生を被験者にすると2割程度しか出さなかったからです。
公共財があると人々はフリーライドするんだ、と教室で教えていた先生方にとっては、マーウェルたちの研究が経済学研究者への「挑戦」と映ったようです。社会学者の実験はどこかがおかしいのであって、経済理論が間違っているはずがない、という反応です。多くの経済学研究者たちが、公共財供給実験を始めました。社会学者たちの実験は1回のみですが、経済学研究者たちは同じ実験を繰り返します。1回目あたりは社会学者のいうように被験者は半分程度のお金を出すものの、10回目あたりだと1~2割になる、というのです。両陣営、引き分けといったところでしょうか。
スパイト・ディレンマ
これらの研究は、アンドレオーニ(American Economic Review, 1955)らの研究にみられるように、人々には、親切心や他人を思いやる心があり、それで出さなくてもよい時に出すんだ、という方向にむかいました。ただ、私はこの方向に違和感を持ちました。そこで、次のような実験を考えたのです。表1の場合の係数は0.7で1以下です。この係数を1よりも大きくするのです。表2では、係数が1.5の場合を示しています。この場合だと、相手が出そうが出すまいが、10ドル出すのがベストとなります。実験をすると、どの被験者も10ドル出すに違いありません。

カルフォルニア大学から筑波大学に移籍した頃、このタイプの実験をしました。被験者は0から10 の間の整数を選べるのです。しかも、表1の実験を10回した後、表2の実験を10回行う実験と、その順序を逆にした実験も実施しました。表1の場合、被験者はどちらの場合でも約2割程度のお金を出しました。ところが、表2の場合、かなり出す被験者もいればそうでない被験者もいたのです。
出さない被験者の理屈は次の通り。相手が出し自分が出さねば、相手の取り分は15、自分は25となり、両方で出し合う場合の取り分の30よりも少なくなるものの、相手よりも取り分が多くなります。そのように考えるなら、出さなければ相手を出し抜くことができるのです。自己の取り分を減らしてまで相手の取り分をよけいに減らす行為を「スパイト(いじわる)」行動と名付けました。表2で、自分の取り分から相手の取り分を引いた差の表を作成してみると、0ドル出すのがベストとなります。つまり、できるだけ多くのお金を求めるなら「出す」のがベスト、相手を出し抜くのなら「出さない」のがベストとなり、被験者はこの間で心が揺れ動いていると考え、この現象を西條・中村(Journal of Conflict Resolution, 1995)は「スパイト・ディレンマ」と名付けたのです。このディレンマは表1では起こらないことを確かめてみるとよいでしょう。
表1の場合、お金を出す被験者の心根が親切心や利他心で、同じ被験者が表2の場合スパイト行動をとる、という説明で納得する人はあまりいないでしょう。この実験結果をみて、公共財供給実験において被験者は親切心や利他心でお金を出しているのではない、と確信するようになりました。ただ、欧米の研究者は、フリーライドがよいのにもかかわらずそうしない理由を親切心や利他心に頼る、という路線をとり、私たちの研究は、欧米の研究の路線からはずれてしまったのです。
だいぶ後になってからですが、私たちの研究をみたメステルマンたち(Economics Letters, 2001)のグループが、スパイト・ディレンマ実験とほぼ同じ実験を実施し、カナダ人はほとんどスバイト行為をしない、という結果を公表しました。
公共財供給とタカハトゲーム
スパイト・ディレンマ研究が一段落した頃、私たちの関心事は、公共財供給の理論にむかいました。グロブズ・レッジャード(Econometrica, 1977)やそのフォロワーたちは、社会の制度(メカニズム)を上手に作ると、社会的に望ましい(パレート効率な)公共財の供給ができることを示しています。フリーライダー問題は少なくとも理論的に解決済み、という訳です。ただ、彼らは、全員がメカニズムに参加することを暗黙のうちに仮定しています。たとえば、ウォーカー・メカニズム(Econometrica, 1981)の場合だと、各々の個人は数をアナウンスせねばなりません。アナウンスせよといってもアナウンスしたくない、ということができないのです。アナウンスしない人が公共財を使えないようにできる場合ならそれでもよいのですが、地球温暖化の問題のように京都議定書を批准しないアメリカのような国も他国の温室効果ガスの削減からの便益を享受できます。空気に国境はないのですから。つまり、グロブズ・ウォーカー以降のメカニズムデザイナーたちは、いわば、排除できる公共財の問題を暗黙のうちに扱ったのです。私たちは本来公共財の持つ「非排除性」の問題が残されたままだということに気づいたのです。
そこで、参加しなくても公共財からの便益を享受できると想定し、お金を出し合うゲームの前に、そのゲームに参加するのかしないのかという意思決定のステージを付け加えるのです。参加の意味を考えてみましょう。たとえば、表1のゲームの場合、相手が参加しないのならお金を出さないと考えるなら、相手が参加せず、あなたが参加する場合、あなたは迷わず0ドルを出すでしょう。一 方、相手もあなたも参加するのなら、あなたは相手がどちらの戦略をとるのかわからなくなります。あなたにとって、相手が参加しないことと参加し て0ドル出すのとは全く異なっているのです。
西條・大和(Journal of Economic Theory, 1999)は、このような公共財供給の参加ゲームに おいては、全員が参加する仕組みをデザインする のは不可能であることを示しました。この意味で、非排除性を有する公共財供給に関する制度設計の理論は振り出しに戻ることになったのです。
地球温暖化のように公共財の「非排除性」を認めると、そんなに簡単には公共財が供給できないことを知り、落胆してしまった私たちは、実験室の中で何事が起こるのか、検討しようということになったのです。図1のように参加・不参加が選べるゲームを考えます。まず2人が同時に参加す るかどうかの意思決定をします。次に、互いの参加に関する意思決定を知った上で、公共財を作るのにどれぐらいお金を出すのかを決めるのです。

表1などとは異なって、2人の評価関数はコブ・ダグラス型で同じとしましょう。つまり、非線形の評価関数を使うのです。評価関数が非線形なので、表3のように利得表を用います。実際の実験では、お互いに0から24までの間の数値を選 べますが、ここではスペースの都合で0から12までの範囲の利得を示しています。

実験では特定のセルに色を付けたりはしていません。この実験ではお金を出すことを「投資」とよぶことにしました。斜めの灰色のセルがベストリスポンスです。たとえば、相手が出さない とき、あなたは11を投資するのがベストです。読者の皆さんは、ここで数分、利得表とにらめっこしてください。たぶん、相手が8のときに、自分も8を選ぶのがナッシュ均衡であることに気付く でしょう。
ここで図1に戻ってみましょう。2人とも参加 を選ぶと、(8,8)の戦略を選び、お互いの利得は7345となります。相手が参加しないときは、11を選び、自分の利得は2658で相手の利得は8278となります。相手はフリーライディングの利得を亭受するのです。両者ともに参加しなければ、お互いに706の利得をえます。これをもとに、参加・不参加を戦略とするときの利得表を作ると、表4 のようになります。
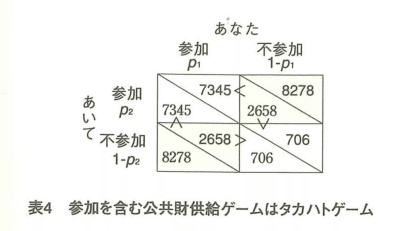
相手が参加するときには不参加、不参加の時には参加がナッシュ均衡となります。相手も自分も参加するのは均衡ではありません。このようなゲームはタカハトゲームとよばれています。つまり公共財の非排除性を考慮に入れるなら、ゲームの構造は四人のディレンマ型ではなく、タカハト型になるのです。タカハトゲームには、混合戦略のナッシュ均衡があり、これは、互いに0.68の確率で参加することです。さらには、この確率が数理生物学者のジョン・メイナード・スミスの開発した概念である進化論的に安定な均衡となります。この意味で、この実験は、進化論的に安定な均衡が実現するのかどうかを検証することとも深く関係しているのです。
日本人は「いじわる」がお好き?!
以上の枠組みで、最初の予備実験をしたのは1995年のことです。当時、住宅金融公庫から筑波大学大学院への派遣院生であった横谷が中心とな って実験を実施しました。1996年秋、ツーソンにて、エコノミック・サイエンス・アソシエーション(実験研究を中心とする学会)の会合でこの研究を報告しました。私たちの報告に強い関心を示してくれたのがケイソン(学術雑誌 Experimental Economicsの編集長〔注:執筆時点〕)です。ここから彼との共同研究が始まることになります。
実験は、日本では筑波大学と都立大学、アメリカでは南カルフォルニア大学(USC)とパーデ ュー大学で実施されました。特定の場所に依存することを排除するために同じ国で複数の大学を選択したのです。今回の実験の場合、同じ国の中ではデータに差がでなかったものの、国の比較になると差がでる、という結果となりました。なお、これまでのほとんどの国際比較研究では各々の国の一カ所でしか実験がなされていませんでした。同じ国の中の複数の場所で実験をする、というのはケイソンのアイデアでした。今後、国際比較実験のスタンダードになるでしょう。
まず、比較のために、全員が参加せねばならな い実験をデザインします。図1の左下の部分です 20人の被験者を同じ教室に集め、2人1組で10組のペアを作ります。ただ、ペアとなった相手が教室のなかでどこにいるのかはわからないようにしています。教室内での話し合いは不可です。まったく同じ実験を15回繰り返しました。回ごとに相 手を変え、同じ相手とは二度と対戦しないように し、これを全員に伝えました。さらには、全員が同じ利得表を持っていることも全員に伝えました意思決定の結果ですが、ペアになった相手の決定はわかるものの、それは他の被験者には知らされないようにしました。以上のデザインをトリートメントAとし、これに加えて、参加の意思決定のできる実験をトリートメントBとしました。
トリートメントAの実験結果をみましょう。ここでは、筑波とUSCを比較しましょう。被験者たちは、もちろんナッシュ均衡なる概念を知りませんが、(8,8)あたりに落ち着くことをなんとなく理解します。ただ、相手が8を選ぶとするな ら、自分が8を選ばずに7を選ぶと、自分の利得は7345から7340に5単位減るものの、相手は7345から6526に減ることに気づき、そのようにするのです。まさにスパイト行動です。
10組のペアで15回繰り返すので、150個のデータがあります。このうち、筑波の場合、ナッシュ均衡の(8,8)は36個、(8,7)は35個、USCの場合、(8,8)は29個、(8,7)は26個です。筑波の平均投資数は7.24、USCのそれは7.75で、それほどの差ではないものの、有意に筑波のそれがUSCに比して低いのです。
参加の意思決定ができるトリートメントBの筑波とUSCの実験結果をみましょう。もし進化論的に安定的な均衡の予測する0.68が正しいとするなら、両者ともに参加するのは、46%(=0.68×0.68×100)、片方のみ参加するのは44%、両者ともに参加しないのは10%となります。150個のテータのうち、たとえば、(8,7)も(7,8)も同じデータとして扱います。つまり、(大きい投資数、小さい投資数)とするのです。こうして150個のデータの分布を示したのが図2です。

筑波の場合、両者ともに参加した場合、一番好度の多いのは(8,8)ではなく、(8,7)です。一方、片方のみが参加した場合、一番多いのは最適反応の11ではなく、なんと7です。両者ともに参加しなかった場合のデータ数は18でした。相手が参加しないことを知った後で、11ではなくなぜ7を選んだのでしょうか。表3をみればわかるように、11を選べば、自分の利得は2658、相手の利得は8278となります。一方、7を選べば、自分の利得は2210となり448減少するものの、相手の利得は4018となり4260減少します。つまり、自己の利得を犠牲にしてまでも、参加をしない相手の利得が大幅に下がるような戦略を選択したのです。
USCの場合には、相手が参加しなかった場合の行動が筑波と異なっています。その場合にでも参加をした被験者は自己の利得を最大にする11を選んでいます。もちろん、7を選んでいる被験者も若干名います。「相手は相手、私は私」といっ たところでしょうか。
トリートメントBの場合のスパイトはAの場合のスパイトとは少し異なっています。Aの場合は相手がどのような行動をとるのかがわからずにス パイト行動をしているので、いわば、純粋なスパ イト行動です。一方、Bの場合は、相手が参加しないことに腹を立て、懲罰的にスパイト行動をすると考えることができます。経済環境で数多くの国際比較実験がありますが、この研究のように、明白に差がでたのはめずらしいといってよいでしょう。
話はここにとどまりません。USCの参加率は最初から最後まで68%の周辺で推移したものの、筑波の場合、それが最初は4割でしたが、最後の5回では85~95%となったのです。公共財をみんなで作ろうとすると、日本人は「ただ乗り」をめざすものの成功しません。というのは、参加をした人が、参加をしなかった人の足を引っ張るからです。これを経験してしまうと、後で参加せざるをえなくなるのです。日本の社会ではみんなで仲良く協力してコトにあたってるのではなく、協力 しないと後が怖い、というところでしょうか。
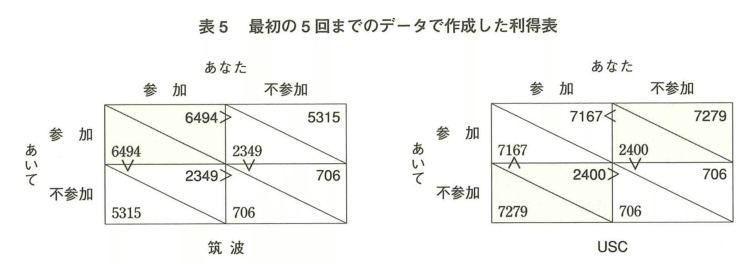
表5は実験の1回から5回における実際の平均利得を示しています。筑波の場合、もともとはタカハトゲームであったのにもかかわらず、被験者のスパイト行動を通じて、両者とも参加するのが ベストというゲームに変容しています。一方、USCの場合、平均利得は変化するもののタカハトゲームの構造自体は変化していません。なお、上記の日本の実験はケイソン・西條・大和・横谷論文(Games and Economic Behavior, 2004)、日米比較実験はケイソン・西條・大和論文(Experimental Economics, 2002)として公刊されています。
20世紀型の経済学から21世紀型の社会科学へ
少し極端かもしれませんが、時や場所にかかわらず、他人との関係ではなく自分のことだけを考える利己的な個人から構成されるモデルで経済活動はほぼ説明できる、と暗黙のうちに仮定してきたのが20世紀型の経済学です。ところが、実験研究が進むにつれて、20世紀の最後あたりから、そうではないらしいことがわかりはじめました。
経済学における限界革命の担い手の一人であったジェボンズは、人間の「こころ」から派生する「感情」を直接計測することはできないとして、計測できる数量情報のみに頼って理論を構築するという方法論を採用しました。19世紀後半のことです。この手法では、人々の評価をブラックボックスとして扱い、人々が「合理」的に行動すると 仮定するのです。人々がどのように評価を形成したのかを問うことなく理論構築を行ったのが20世紀型の方法でした。20世紀型の研究者は、利己的 な個人を仮定し評価を与件とするという大胆な〈簡便法〉で理論を構築し一定の成功を納めるものの、なんとこれが〈伝統〉になってしまったのです。
一方、これに先立つ18世紀の研究者、たとえばアダムスミスやディビット・ヒュームは、他者との関係をもっともっと重視していました。ある意味では、実験研究者は、人間は他者との微妙な関係でさまざまな評価をしていることを再発見しているといってよいのかもしれません。さらには、ニューロエコノミストとよばれる先鋭集団は、脳をスキャンすることによって、ブラックボックスをこじ開けようとしています。「スパイト」をする遺伝子の発見につながる研究もありえるはずで「マキャベリ的知性仮説」とよばれる仮説が人類学者、進化論の研究者、さらには認知科学者な どに支持されています。ヒトはなぜ賢くなったのか、を問うのです。相手を騙し、欺き、出し抜くことによって知性を進化させた、という仮説です。私たちのいう「スパイト」行動もこの仮説につながりを持つはずです。
このような視点から、私たちは、「日本人はいじわるがお好き?!」プロジェクトを立ち上げ、新たなコントロールのもとで公共財に限らずオークションなどを含む理論・実験研究を継続し、さらにはf-MRIを用いて被験者の脳をスキャンし始めています。
参考文献
[2.公共財供給と囚人のディレンマ]
Issac, R. M. and J. Walker, (1988), "Group Size Effects in Public Goods Provision: The Voluntary Contributions Mechanism," Quarterly Journal of Economics, 103, p. 179-199 Marwell, G. and R. Ames, (1981), "Economists Free Ride, Does Anyone Else?" Journal of Public Economics, 15, 295-310.
[3. スパイト・ディレンマ]
Andreoni, J. (1995), "Cooperation in Public Goods Experiments: Kindness or Confusion?" American Economic Review, 85(4), 891-904.
Saijo. T., and H. Nakamura (1995), "The 'Spite' Dilemma in Voluntary Contribution Mechanism Experiments," Journal of Conflict Resolution, Vol.39(3), 535-560.
Brunton, D., R. Hasan, and S. Mestelman (2001), "The 'spite dilemma: Spite or No Spite, Is There a Dilemma?" Economics Letters, 71(3),405-412.
Ledyard, J., (1995). "Public Goods: Some Experimental Results", Ch.2 in John Kagel and Alvin Roth (Eds) Handbook of Experimental Economics, Princeton University Press.
[4公共財供給とタカハトゲーム]
Groves, T., and J. Ledyard (1977), "Optimal Allocation of Public Goods: A Solution to the Free Rider Problem." Econometrica, 45,783-811.
Walker, M. (1981), "A Simple Incentive Compatible Scheme for Attaining Lindahl Allocations." Econometrica 49, 65-71.
Saijo. T., and T. Yamato (1999). "A Voluntary Participation Game with a Non-Excludable Public Good," Journal of Economic Theory, 84, 227-242.
[5. 日本人は「いじわる」がお好き?!]
Cason, T., T. Saijo, T. Yamato, and K. Yokotani (2004), "Non Excludable Public Good Experiments," Games and Economie Behavior.49(1),81-102.
Cason, T., T. Saijo, and T. Yamato (2002), "Voluntary Participation and Spite in Public Good Provision Experiments: An International Comparison, Experimental Economics 5. 133-153.
Brandts, J., T. Saijo, and A. Schram (2004), "A Four Country Comparison of Spite, Cooperation and Errors in Voluntary Contribution Mechanisms," Public Choice 119 (3-4), 381-424.
Saijo, T., "Spiteful Behavior in Voluntary Contribution Mechanism Experiments," forthcoming in Handbook of Experimental Results, Eds., Charles Plott and Vernon Smith.
いいなと思ったら応援しよう!


