
論理学(特に命題論理)は自然言語の一般化ではない
私は、拙著
A→Bが「正しい」とはどういうことなのか ~真理(値)表とは何なのか
http://miya.aki.gs/miya/miya_report40.pdf
・・・の第7章において、命題論理は電子回路と電流が流れるかどうかの関係として捉えることができるが、一方その論理は私たちの日常生活における真偽判断とは異なるものであることを述べた。
論理学は私たちの日常的な真偽の判断に基づくものではない。むしろ特定の回路において電流が流れるか流れないかの判断に基づく学問、真偽ではなく電子回路に関する学問だと捉えるべきだいうことなのである。
論理学の面白味は、自然言語に根ざしながらもそこからどんどん一般化を進めていくというところ
・・・という考え方は全くの的外れなのである。論理学は自然言語に根ざしてなどいない。部分的に拝借はしているが(ここが論理学の正確な位置づけを見えにくくしている)。自然言語を根拠に説明しようとするから私たちの日常生活における真偽判断と齟齬をきたしてしまうのである。それらの齟齬は条件法や選言において顕著である。
論理学における命題論理とは、例えば2変数の真理関数において
表1:2変数の真理関数が全部でいくつあるか
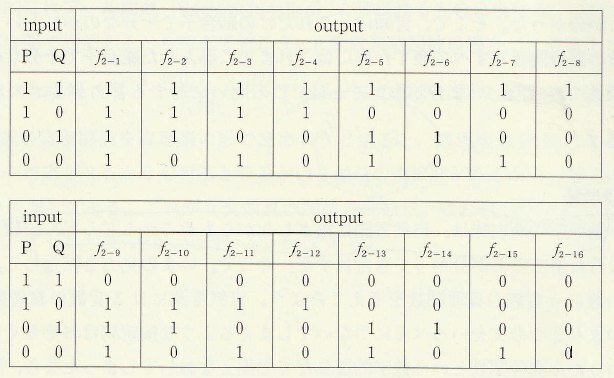
・・・というふうに16通りのoutputを表現できる関数(人工言語)を制作していく、取り決めていくプロセスなのである。まずこの前提が先にあるわけで、私たちの日常的真偽判断とは別物なのだ。上記の表は1と0いう記号の組み合わせが16通りあるという事実のみを示しているのであって、1と0とが真/偽と対応していることは全く前提されていない。そもそも”真理関数”でさえないということである。
そして先に述べたように、1と0を、真/偽ではなく、電流が流れている/流れていない、という電子回路の問題として捉えれば全く齟齬なく命題論理を理解・解釈することができるのである。
日常言語→一般化→命題論理、ではなく
電子回路の電流on/off(命題論理)→日常言語や数学理論との擦り合わせ
・・・実際のところコンピュータ関連の業界では後者のプロセスで作業(?)が進んでいると思うのだが、いかがであろうか?
このように割り切って考えれば、健全性や完全性について非常にすっきりした形で理解できるのではないだろうか。もしウカシェビッチの公理系などで躓いている人がいたら、このように解釈してみることをお勧めする。
