線を引く - 単純そうに見える奥の深い世界
むかしむかし、グラフィック画面に点を打つのに、自分でアドレスを計算して直接VRAMに値を書き込むことで点を打つ話を以下の記事に書きました。
自分で点を打つ世界
点ですら自分で打たなくてはならなかったくらいなのですから、当然のように線も自分で引かないとなりません。線というのは2つの点を結ぶものですから、2つのXY座標を指定して線を引きます。学校でならったと思いますが、直線の方程式は
Y = mX + nですから、2つの点(X0,Y0)と(X1,Y1)を満たすmとnを計算して、XからY(またはYからX)を求める式を作ります。
Y = (Y1 - Y0) / (X1 - X0) ✕ (X - X0) + Y0これでXをX0からX1に変化させながらYを求めて線を描いていけばいいはずです。
【高校】直線の方程式5パターンの求め方をイチから!
大したことは無いじゃないと見えるかもしれませんが、実際に画面に直線を描くには、あまり効率の良い方法ではありません。そもそも小数のまま計算なんてしていたら、昔のCPUにとっては重いことこの上ありません。
線分の描画
直線なのでひとつ前の点から大きく値が変わることはないので、前の座標を計算した結果との差だけを考慮したほうが処理が速くなるわけです。
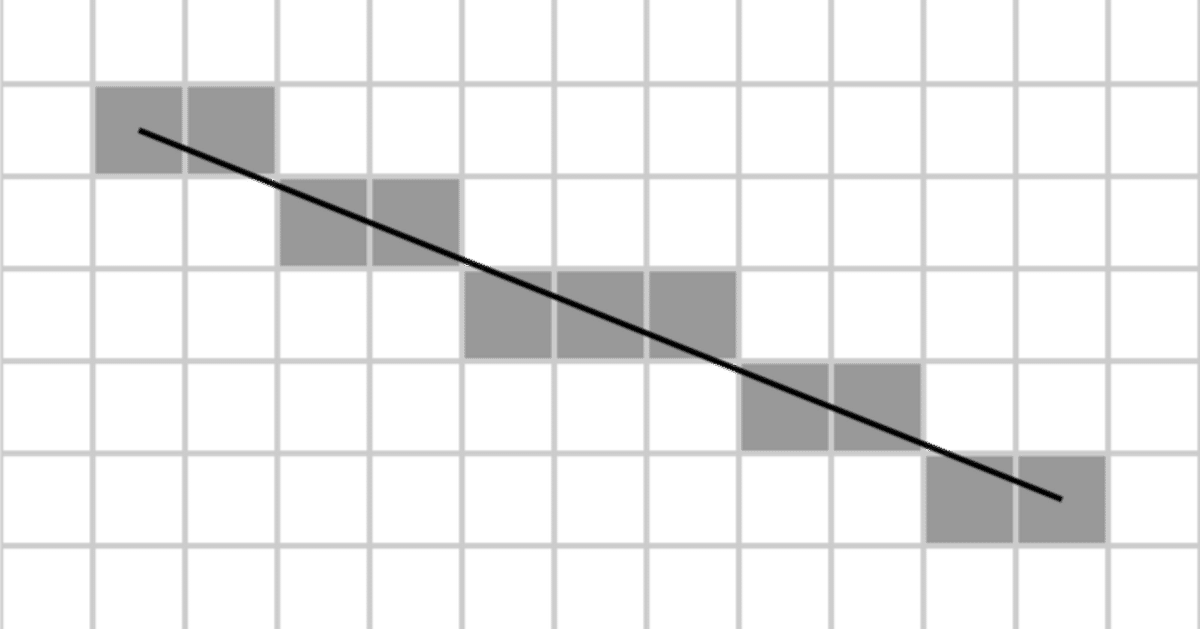
ブレゼンハムのアルゴリズム
整数で処理すると丸め処理が見た目に大きく影響します。特に解像度が320✕200とかであれば、ひとつの点がハッキリと目に見えるわけですし、単純に計算するだけではデコボコが目立つこともあります。傾き次第でひとつのXに対して複数のYの点を打たないと繋がって見えない場合もあるわけです。
線を引くのなんて簡単だ !?
もっと細かいことを言えば、傾きの小さな線であれば横方向の点は同じアドレス(1バイトで8点分とか)の値に含まれることが多いので、これを1度の処理で済ませたくなります。これとは逆に傾きが大きい時は端数処理の関係で縦棒に近い場合はオーバーフローしないような配慮も必要です。こうして単に線を引くだけでアレコレ考える羽目になるんですね。
ふぞろいの段差たち
これで単純な線は引けるようになるわけですが、カラーの場合、複数のプレーンに対する処理をしたり、実線ではなく点線で引きたい、それもいろいろな点線のパターンを使いたい、太さも選べるようにしたいと次々と要求が増えてきて、それぞれの場合に無駄な処理が無いか、コードをニラメッコしてより高速な処理を目指すわけです。
プログラマーとしての生い立ち
直線に関してはPC-9801などではGDCと呼ばれる専用のグラフィック処理を行うチップが追加されていて、そちらにパラメタを渡せば高速に処理を行ってもらうことも出来るようになったのですが、それでも今度は曲線を引こうとすれば、やはり手で値を作っていかなければなりません。グラフィック処理は結果が直ぐに目の前にでるだけに、パフォーマンスが求められることも多く、システムが提供してくれたり出来合いのコードを使うと汎用的なだけに、遅くなってしまうことも多く、アセンブラで書くにしても速度を稼ぐために命令のクロック数を数え、インダイレクトやインデックスを使うと遅くなると自己書き換えまでしてコードを書いていました。
解像度が上がって色数も増えてくると、今度はアンチエイリアスという手法で線を綺麗にひこうとするのですが、これもちょっと面倒で、さすがにあり物をいただくようになりました。
ドット絵似非講座 (2) 直線と曲線
いやあ、線だけでも奥が深いですね。線が済むと、今度は面というか塗りつぶすにもいろいろなテクがありました。その辺りはそのうち思い出します。実は、プログラムを書くのに特定のジャンルを除くと、あまり数学を使うことは出てこないのですが、グラフィックをやるときは教科書を引っ張り出す羽目になることも多いです。そういえば、ちょうどインターフェース誌でも特集されているようです。
Interface 2024年4月号
ヘッダ画像は、以下のものを使わせていただきました。https://commons.wikimedia.org/wiki/File:Bresenham.svg
Crotalus horridus - I created this SVG file using Notepad, according to the official specification. Inkscape was used to verify that it was rendering properly., パブリック・ドメイン, https://commons.wikimedia.org/w/index.php?curid=3243491による
いいなと思ったら応援しよう!

