UU_Rhino会＃１ parametric design

rhinocerosというか主にgrasshopperを使って、２次元のパターン生成の練習をしていきました。

１目的

grasshopperを使って、parametrical designの導入っぽい二次元模様を作ってそこから色々応用していきたい。

２作ったものとGHのコンポーネントデータ

↓rhino側

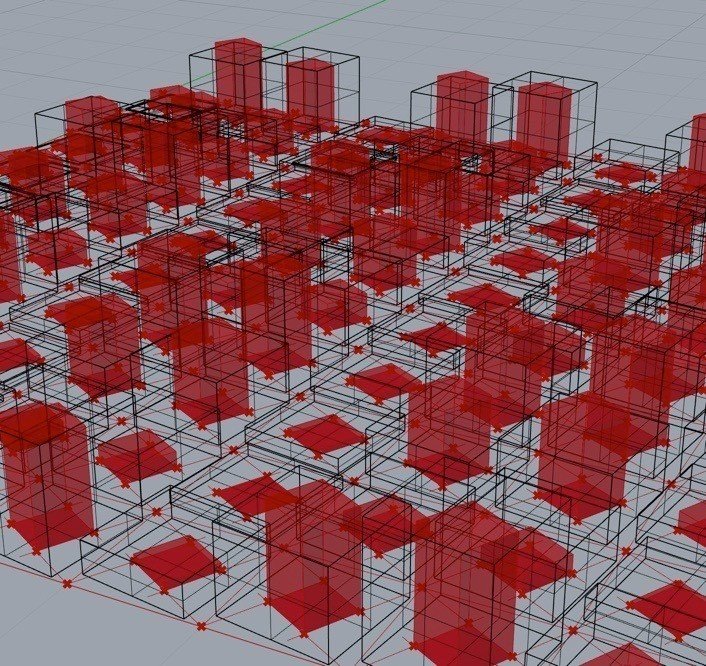
grasshopper側

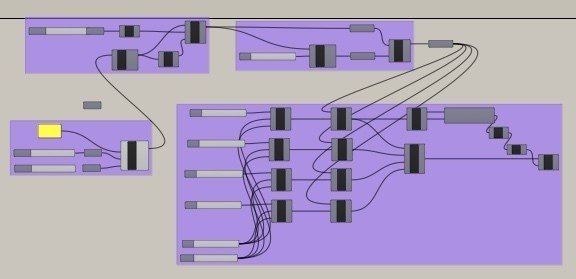
３製作手順

１. １０×１０の四角形を作る

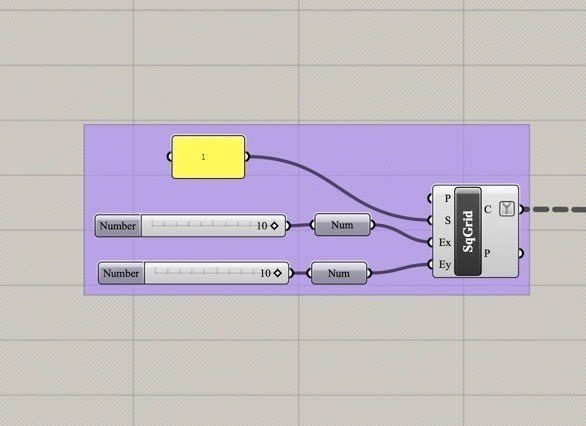
SqGrid(square)<Grid<Vector
num(number)<Primitive<Params
Number(slider)<Input<Params

まずは１０×１０のグリッドを持った四角形を作ります。（左下の四角形は無視してください）

後から気になったのですが、squareコンポーネントの出力部のcとpはcurveとpointによる出力ができるそうなのですがどのように出力されているのか調べてみました。

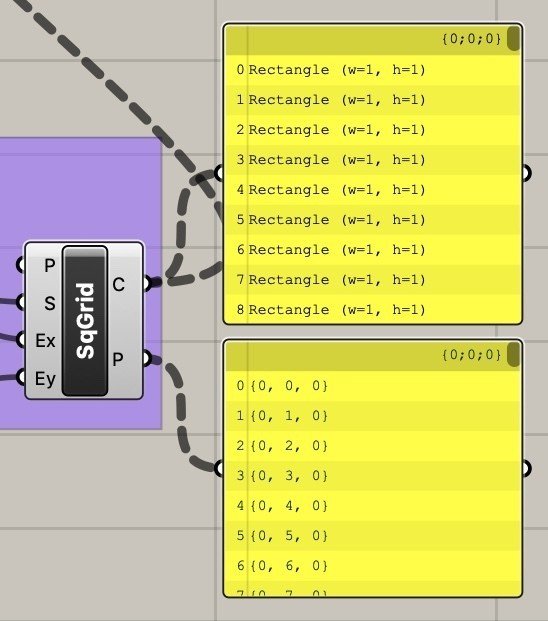
curveの方の出力は、１００個の辺的な出力ではなく１００個の四角の線的な出力であると分かりました。pointの方の出力は予想通り１００個の点が出力されていました。

このまま進めていってもいいのですが、コンポーネントの出力部Cの上で右クリックしてsimplfyというものを使うとリストの中の無駄な部分を削ってシンプルにしてくれるのでオススメです。（ただ使うと今回の場合階層が一番下から一番上に上がってくるので、他のリストと対応させるときに注意が必要です。）

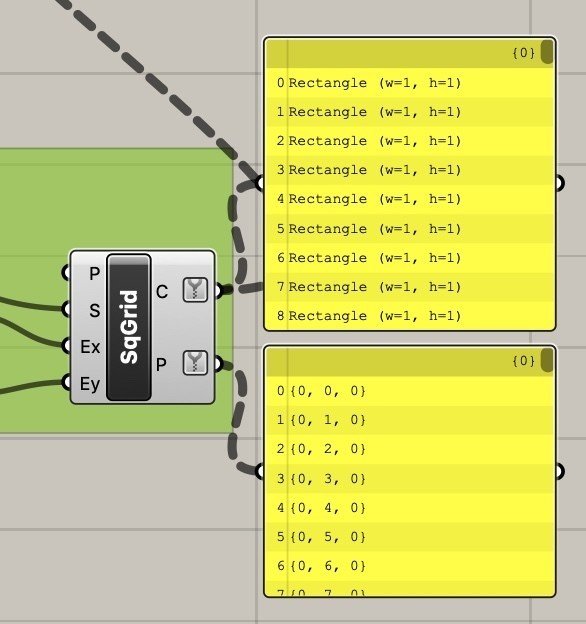
パネルの右上の{0,0,0}が{0}になっているのが分かると思います。

２. １のspuareコンポーネントの出力cからcurveのリストを取得して、パターンを製作していく

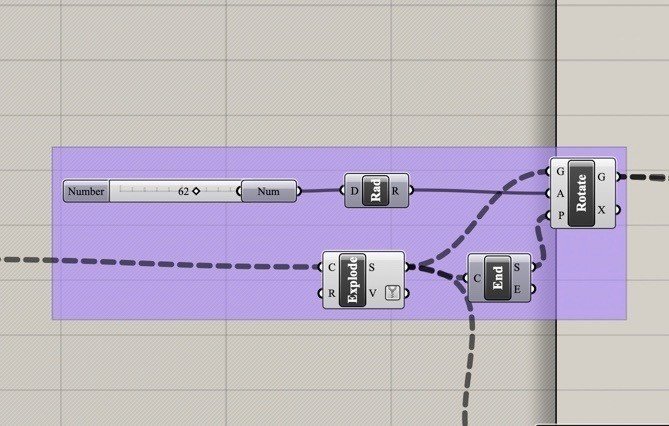
Rad(Radians)<Trig<Maths
Explode<Util<Curve
End(End points)<Analysis<Curve
Rotate<Euclidean<Transform

Explodeは受け取った四角の線を４つの辺に分割して、Sに出力してくれます。なのでSには４００個の辺のデータリストが出力されます。この400個のデータに対してEndコンポーネントを使って、端点を出力します。この端点２つの片方を軸として、400個それぞれの辺を回転させて模様を作っていきます。ここで気をつけたいのは、RotateのA（angle）はradiansの形で入力しないといけないので、度数をRadコンポーネントを通してradiansの形にする必要があります。Aの上で右クリックからdegreeボタンを押して、度数入力できるようにすることもできます。

３. 各curveに対して交点を取得していく

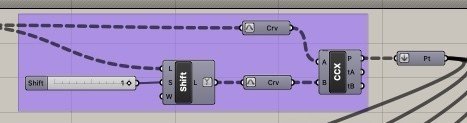
Crv(Curve)<Geometry<Params
CCX(Curve || Curve)<Physical<Intersect
Shift(Shift List)<List<Sets
Pt(point)<Geometry<Params

ここではCCXコンポーネントを使いcurveとcurveの交点を求めて、交点の点のリストにしてまとめていきます。Ptの↓のマークは、「Flatten」で階層を一つ上にあげます。なので無駄に分離しているものを一つのまとまりに戻すイメージになります。

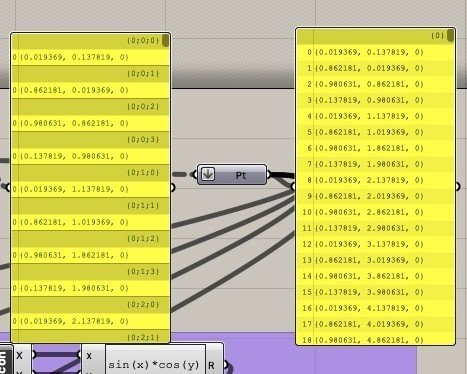
分離していたものが、一つのまとまりになっていることが分かると思います。

ちなみにcurveコンポーネントの横にあるニョロっとしたマークはreparameterizeというものです。以下が詳しい説明です。

Q3.[Reparameterize]（正規化）とは何ですか？
A.[Reparameterize]とは「再定義する」という意味。この再定義を行なう事で、サイズや形状の異なるカーブやサーフェスを同一規格で扱える様になります。Grasshopperではこの[Reparameterize]（正規化とも言う）を行なうと、どの様なカーブのパラメーター[t]も、始点を[0]、終点を[1]として再定義します。サーフェスの場合も、サーフェスは[U]方向と[V]方向にそれぞれ伸びたカーブが格子状に配置された物という認識が出来る為、[U]方向と[V]方向のカーブそれぞれのパラメーター[t]について、始点を[0]、終点を[1]として再定義する事で、カーブと同様に扱える様にしています。

要は、バラバラになった線の始点と終点を揃えるイメージで「正規化する」っていいます。（書いてて覚えた（笑））

４.  交点４つを使って平面をつくりそこから波っぽい表現をします。

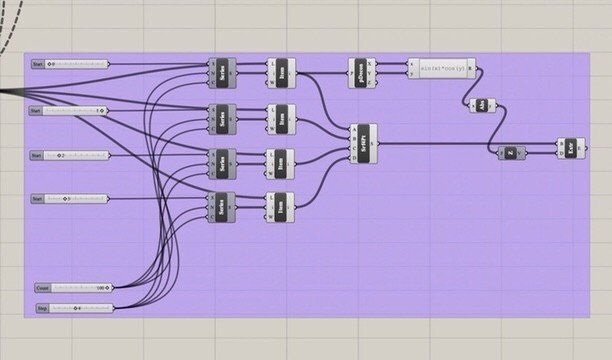
Shift(Shift List)<List<Sets
Item(List Item)<List<Sets
Srf4Pt(4Point surface)<Freeform<Surface
pDecon(Deconstruct)<Point<Vector
Expression<Script<Maths
abs(absolute)<Operators<Maths
Z(Unit Z)<Vector<Vector
Extra(Extrude)<Freeform<Surface

ここが複雑に見えてかなり簡単な仕組みです。交点のリストの中から、０−３番目の交点データで面を作り、次は４−８番目のデータで面をつくる...ということを繰り返していきます。なのでオリジナルのリストを４つに分けて、１つ目は0,4,8,12...のデータを持つリスト、次が1,5,9,13...のデータを持つリスト、2,6,10,14...のデータを持つリスト、3,7,11,15...のデータを持つリストという風に決めると、各リストから１つずつ取っていくと最初が0,1,2,3のデータで面を作り、次に4,5,6,7で面を作りというように上手く作り出していることがわかります。

最後にExpressionコンポーネントを使って、三角関数の計算をしてくれるようにしてExtrudeコンポーネントで押し出しをしました。

三角関数を弄ったり、回転のパラメータを弄ったり↓

製作してて思ったのが、ビルの高さを三角関数に沿って、作り出すと景観が見やすかったり、風の流れが良いなと感じました。実際のビルの作り方では実用性はないかもしれませんが、トヨタのように一から全部決めた上で街を作り出すときはこういった手法で高さを決めるのも街のParametricalDesignかもしれませんね。