債券ポートフォリオ

債券価格変化率の近似

• 次に残存期間が短い債券が示されていない場合は、「短期金利」、「ゼロ」を使用する。

• 超過リターン＝キャリーリターン＋ロールダウンリターン

• トータルリターン＝超過リターン＋短期金利

「利回りベースのロールダウン」といえば修正Dを除いて計算する

バタフライトレード

利回り曲線の曲率の変化を想定した戦略である。

• 利回り曲線の曲率が増加すると想定するなら、曲率の変化のエクスポージャーがプラス値の国債をロング、マイナス値の国債をショートする。

モ－ゲージ･バック証券は、期限前返済額が変動する特徴がある。
その原因は、金利低下による借り手のローン借り換えなど。

インフレ連動債

イールドカーブ・金利の期間構造

利回り変化幅のマイナス度合いが大きいほどリターンは高くなる

純粋期待仮説
フォワードレートは、将来のスポットレートの期待値に等しい。

リスクプレミアム仮説
短期債に比べて長期債は金利変動に伴う価格リスクが大きく、これに見合ってきたんリターンが高くなる。フォワードレートは、将来の予想短期金利にリスクプレミアムを加えたものになる。

特定期間選好仮説
投資家や借り手が選好する期間は経済主体や目的ごとに異なる。

市場分断仮説
特定の満期セクター内での需給関係によって金利期間構造が異なる。

ポートフォリオ構築方法

フルキャップ法
インデックス採用銘柄すべてを保有するポートフォリオを構築する方法。

層化抽出法
銘柄種別や残存期間などで区切った区切ったセクターごとに個別銘柄を抽出し、ポートフォリオを構築する方法。

最適化法
制約条件の下、何らかの目的関数を最適化する解を求めることによって銘柄を選択し、ポートフォリオを構築する方法。

債券運用

年金運用などの場合、負債とのマッチングを図るパッシブ運用が行われることが多い。

• キャッシュフローマッチング

• デュレーションマッチング

■キャッシュフローマッチング（デディケーション運用）
負債のキャッシュアウトフローと資産のキャッシュインフローを時期、金額ともに一致させる。
原理的には単純でデフォルトがなければ確実な支払いが可能となるが、キャッシュフローの支払日に完全に合致するような債券銘柄の選択が困難。

■デュレーションマッチング（イミュニゼーション運用）
資産の金利感応度（修正デュレーション）を負債の金利感応度（デュレーション）に一致させる。サープラスを安定させる。
債券銘柄の選択が柔軟で債券ポートフォリオの組成が比較的容易であるが、資産と負債のデュレーションは期間の経過に伴って乖離してくるため債券ポートフォリオのリバランスが必要。

イールドカーブの変化

オプション内蔵型債券

実効デュレーション

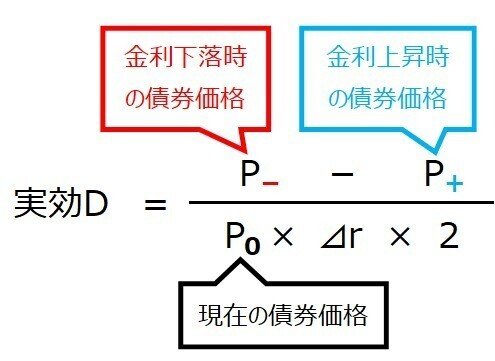
物価連動国債

• 想定元金を調整する連動係数は現在1.000

• 1年後に連動係数が1.010に上昇

物価変動国債の1年間のリターンはいくらか。

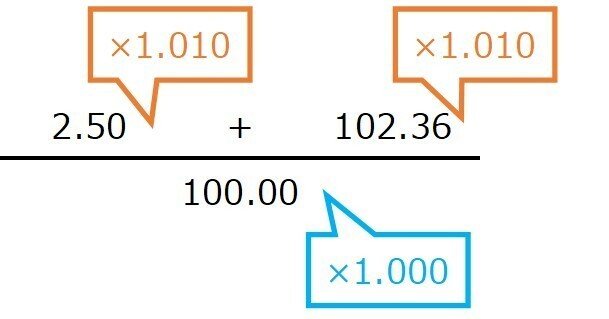
• クーポンレートと1年後の債券価格に連動係数1.010を掛ける

• 現在の名目価格は現在の連動係数1.000を掛ける

キーレートデュレーション

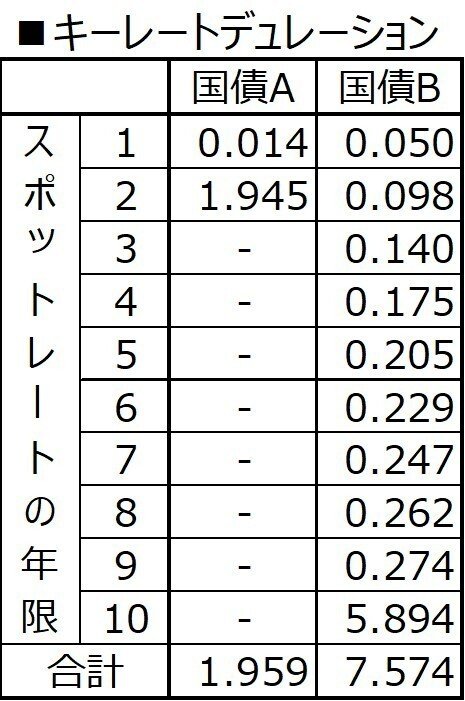
国債Bが①のように変化した時の価格変化率
↓
▲7.574×(＋0.05)＝▲0.38％
●水準変化の場合はキーレートデュレーションの合計を使用
●キーレートデュレーションの合計×水準変化幅でOK
●ただし、KRDの符号は逆にすることを忘れない

国債Aが②のように変化した時の価格変化率
↓
▲0.014×(▲0.04)＋▲1.945×(▲0.03)＝＋0.06％
●傾き変化の場合は各スポットレートを使用
●KRDの符号を逆にすることを忘れずに

利付債の最終利回りは全ての期間に共通の割引率でありフラット。
スポットレートは通常、短期が低く長期が高く右上がり、しかも中期ぞ^んに膨らみがある場合が多い。
このため、フラットな利付債の最終利回りに基づいた修正デュレーションと、フラットではないスポットレートに基づいたキーレートデュレーションの合計は完全には一致しない。