OpenFOAMでシュレーディンガー方程式の検討

オープンCAEのアドベントカレンダー2023の投稿記事です。

オープンCAEのカレンダー | Advent Calendar 2023 - Qiita

はじめにこちらの記事は自分のメモなので、全く有益な情報はないかもしれません。

それにうまくいっていません(笑)
というか言い訳をすると、ちょっと考えて、ちょっとやってみたという程度です。
ゆえに、進捗程度にお聞きください。

やりたいこと

やりたいことは本記事のタイトル通りです。

OpenFOAMは流体解析のオープンソースとして有名です。
流体解析がメインですが、偏微分方程式解法がクラスとしてまとめられていたりするので、原理的にはどういった偏微分方程式もカスタマイズして使用することができるはずです。

そこで、量子力学の基礎の方程式となるシュレディンガー方程式をOpenFOAMでできないかを考えます。

シュレディンガー方程式を書くと以下のような、複素関数の時間発展の式です。

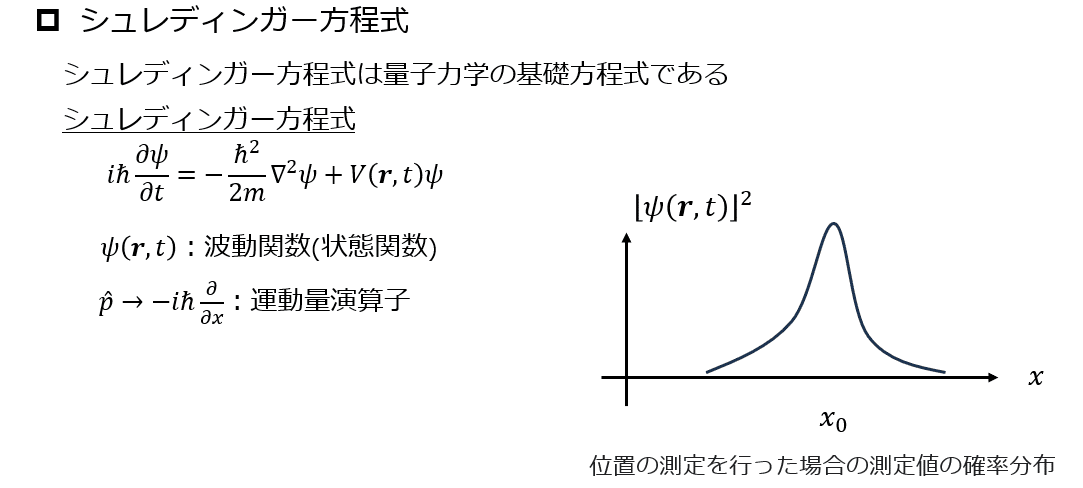
シュレディンガー方程式は全く流体と関係がないわけではなく、似た形でグロスピタエフスキー方程式と呼ばれる多体系のボース粒子が従う方程式があります。

グロス＝ピタエフスキー方程式 - Wikipedia

グロス＝ピタエフスキー方程式（グロス＝ピタエフスキーほうていしき、英: Gross–Pitaevskii equation; GPE）は、ボソン間相互作用が擬ポテンシャルとして表される理想的なボソン多体系の、ハートリー＝フォック近似の下での基底状態を記述するモデルである。

上記の方程式はボース＝アインシュタイン凝縮体の一粒子波動関数に対するモデル方程式となっている。グロス＝ピタエフスキー方程式はギンツブルグ＝ランダウ方程式と似た形をしており、また非線形シュレーディンガー方程式として言及されることも多い。

説明は端折り気味ですが、ここから量子流体という量子力学的な効果を持った流体現象を引き越します。
シュレディンガー方程式方程式は1粒子の確率密度に関係した関数が従う方程式ですが、グロスピタエフスキーは多体系の数密度が従う方程式です。
ですが、以下に示すように粒子間の相互作用が加わっただけでほとんど式はシュレディンガー方程式です。

量子力学的効果と言われているのは、上記のグロスピタエフスキー方程式から、ナビエストークス方程式と似た式を導くことができることから来ており、量子力学的な流体現象を示唆しています。

詳しくは、書籍でどうぞ_(._.)_

量子流体力学

いきなり難しいことはできないので、まずはシュレディンガー方程式ができないか考えてみます。

※先に言っておきますが、現状できていません！
が、少しだけ考えたので良い方法があれば是非ともトライして共有してください_(._.)_

OpenFOAMでシュレディンガー方程式を考える

似たような例がないか探すと・・・・ありました。

Nonlinear Schrödinger Equation

さらに、実装方法はこちらを参考にできそうです。

まず、シュレディンガー方程式を方程式は複素関数を扱う式であり、式の中に虚数が入っています。
OpenFOAMには

•  volScalarField：圧力、温度、エネルギーなど

•  volVectorField：流速など

のようなクラスが存在しており、基本的に実関数を扱うクラスです。

volComplexScalarFieldみたいなものがあればいいですよね。
仮にあったとしても、OpenFOAMで用意されている行列式を解くことができるのか怪しいです。

そこで、実部と虚部に分けることを考えます。

これで、解くべき方程式は実関数のみになりました。

laplacianFoamをカスタマイズ

ほとんどlaplacianFoamと同じ式なので、適当にカスタマイズします。
laplacianFoamをMylaplacianFoamにコピーして編集していきます。

Make/files

MySchroedingerFoam.C

EXE = $(FOAM_USER_APPBIN)/MySchroedingerFoam

MylaplacianFoam.C

#include "fvCFD.H"
#include "fvOptions.H"
#include "simpleControl.H"

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

int main(int argc, char *argv[])
{
    argList::addNote
    (
        "Laplace equation solver for a scalar quantity."
    );

    #include "postProcess.H"

    #include "addCheckCaseOptions.H"
    #include "setRootCaseLists.H"
    #include "createTime.H"
    #include "createMesh.H"

    simpleControl simple(mesh);

    #include "createFields.H"

    // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

    Info<< "\nCalculating temperature distribution\n" << endl;

    while (simple.loop())
    {
        Info<< "Time = " << runTime.timeName() << nl << endl;

        while (simple.correctNonOrthogonal())
        {
            // solve(fvm::ddt(T) - fvm::laplacian(DT, T));

            fvScalarMatrix PsiRealEqn
            (
                fvm::ddt(PsiImg) - fvc::laplacian(DThbar/(2*mass), PsiReal)
             //==
             //   fvOptions(PsiImg)
            );

            //add
            /*
                fvcにして陽解法にしている
                空間微分にクランクニコルソン法を適用する場合は、fvc::laplacian(DT, Ti)ではなく
                0.5*( fvm::laplacian(DT, Ti) + fvc::laplacian(DT, Ti) )
                のように、TnとToの平均を計算するようにする
            */
            fvScalarMatrix PsiImgEqn
            (
                fvm::ddt(PsiReal) + fvc::laplacian(DThbar/(2*mass), PsiImg)
             //==
             //   fvOptions(PsiReal)
            );

            //fvOptions.constrain(PsiRealEqn);
            PsiRealEqn.solve();
            //fvOptions.correct(PsiReal);

            //add 
            //fvOptions.constrain(PsiImgEqn);
            PsiImgEqn.solve();
            //fvOptions.correct(PsiImg);
            //add end
        }

        forAll(PsiReal,i)
        {
            absPsi[i] = sqr(pow(PsiReal[i],2) + pow(PsiImg[i],2) );
        }
        //Info << "absT : " << absT << endl;
        
        //#include "write.H"
        runTime.write(); //add
        runTime.printExecutionTime(Info);
    }
    
    Info<< "End\n" << endl;

    return 0;
}


// ************************************************************************* //

createFields.H

Info<< "Reading field PsiReal\n" << endl;

volScalarField PsiReal
(
    IOobject
    (
        "PsiReal",
        runTime.timeName(),
        mesh,
        IOobject::MUST_READ,
        IOobject::AUTO_WRITE
    ),
    mesh
);

Info<< "Reading field PsiImg\n" << endl;

volScalarField PsiImg
(
    IOobject
    (
        "PsiImg",
        runTime.timeName(),
        mesh,
        IOobject::MUST_READ,
        IOobject::AUTO_WRITE
    ),
    mesh
);

volScalarField absPsi
(
    IOobject
    (
        "absPsi",
        runTime.timeName(),
        mesh,
        IOobject::READ_IF_PRESENT ,
        IOobject::AUTO_WRITE
    ),
    mesh
);

Info<< "Reading diffusivity DT\n" << endl;

volScalarField DT
(
    IOobject
    (
        "DT",
        runTime.timeName(),
        mesh,
        IOobject::READ_IF_PRESENT,
        IOobject::AUTO_WRITE
    ),
    mesh,
    dimensionedScalar(dimViscosity, Zero)
);

Info<< "Reading diffusivity DThbar\n" << endl;

// m/s
dimensionSet dimhbar(1, 2, -1, 0, 0, 0, 0); // [kg m s K mol A Cd]

volScalarField DThbar
(
    IOobject
    (
        "DThbar",
        runTime.timeName(),
        mesh,
        IOobject::READ_IF_PRESENT,
        IOobject::AUTO_WRITE
    ),
    mesh,
    dimensionedScalar(dimhbar, Zero)
);

Info<< "Reading mass\n" << endl;

volScalarField mass
(
    IOobject
    (
        "mass",
        runTime.timeName(),
        mesh,
        IOobject::READ_IF_PRESENT,
        IOobject::AUTO_WRITE
    ),
    mesh,
    dimensionedScalar(dimMass, Zero)
);


Info  << "dimhbar : " << dimhbar << endl;
if (!DThbar.headerOk())
{
    IOdictionary transportProperties
    (
        IOobject
        (
            "transportProperties",
            runTime.constant(),
            mesh,
            IOobject::MUST_READ_IF_MODIFIED,
            IOobject::NO_WRITE
        )
    );
    Info  << "dimhbar : " << dimhbar << endl;
    DT = dimensionedScalar("DT", dimViscosity, transportProperties);
    DThbar = dimensionedScalar("DThbar", dimhbar , transportProperties);
    mass = dimensionedScalar("mass", dimMass , transportProperties);
    Info << "mass : " << mass << endl;
//    Info << "DThbar/(2*mass) : " << DThbar.value()/(2*mass.value()) << endl;
}

#include "createFvOptions.H"

• PsiReal：実部

• PsiImg：虚部

• absPsi：絶対値

• DT：デフォルトであった定数（今回は使っていない）

• DThbar：$${\hbar}$$（次元を合わせる必要がある）

• mass：質量（次元を合わせる必要がある）

以上適当にカスタマイズ終了。

ケースファイルをコピー

とりあえず計算できるのかを確認します。

sysem/blockMeshDict

scale  1.0;
xmax 1;
ymax 0.1;
zmax 0.1;

vertices        
(
   ( 0.0   0.0   0.0)
   ( $xmax 0.0   0.0)
   ( $xmax 0.0   $zmax)
   ( 0.0   0.0   $zmax)
   ( 0.0   $ymax 0.0)
   ( $xmax $ymax 0.0)
   ( $xmax $ymax $zmax)
   ( 0.0   $ymax $zmax)
);

blocks          
(
    hex (0 1 5 4 3 2 6 7)   (100 1 1) simpleGrading (1 1 1)
);

edges           
(
);

boundary         
(
    XMin
    {
        type patch;
        faces
        (
            (0 4 7 3)
        );
    }
    XMax
    {
        type patch;
        faces
        (
            (1 5 6 2)
        );
    }
    ZMin
    {
        type empty;
        faces
        (
            (0 1 5 4)
        );
    }
    ZMax
    {
        type empty;
        faces
        (
            (3 2 6 7)
        );
    }
    YMin
    {
        type wall;
        faces
        (
            (0 1 2 3)
        );
    }
    YMax
    {
        type wall;
        faces
        (
            (4 5 6 7)
        );
    }
);

mergePatchPairs
(
);

メッシュは適当にこんな感じです。

system/fvSchems

ddtSchemes
{
    default         Euler;
}

gradSchemes
{
    default         none;
    grad(T)         Gauss linear;
    grad(Ti)         Gauss linear;
    grad(PsiReal)         Gauss linear;
    grad(PsiImg)         Gauss linear;
}

divSchemes
{
    default         none;
    //div(phi,T) Gauss upwind grad(T);
}

laplacianSchemes
{
    default         none;
    // laplacian(DT,T) Gauss linear corrected;
    // laplacian(DT,Ti) Gauss linear corrected;
    // laplacian(DThbar,T) Gauss linear corrected;
    // laplacian(DThbar,Ti) Gauss linear corrected;
    laplacian((DThbar|(2*mass)),PsiReal) Gauss linear corrected;
    laplacian((DThbar|(2*mass)),PsiImg) Gauss linear corrected;
}


interpolationSchemes
{
    default         linear;
}

snGradSchemes
{
    default         corrected;
}

system/fvSolution

solvers
{
    PsiReal
    {
        solver          PBiCGStab;
        preconditioner  DIC;//DILU;
        tolerance       1e-06;
        relTol          0;
    }
    PsiImg
    {
        $PsiReal
    }
}

SIMPLE
{
    nNonOrthogonalCorrectors 0;//2;
}

constant/transportProperties/

/DT              0.001;
DThbar              0.1;
mass              1.0;

0.orig/absPsi

FoamFile
{
    version     2.0;
    format      ascii;
    class       volScalarField;
    location    "0";
    object      absPsi;
}

dimensions      [0 0 0 0 0 0 0];//[0 0 0 1 0 0 0];


internalField   uniform 0.0; 

boundaryField
{
    XMin
    {
        type            zeroGradient;
    }
    XMax
    {
        type            zeroGradient;
    }
    ZMin
    {
        type            empty;
    }
    ZMax
    {
        type            empty;
    }
    YMin
    {
        type            slip;
    }
    YMax
    {
        type            slip;
    }
}

0.orig/PsiReal

FoamFile
{
    version     2.0;
    format      ascii;
    class       volScalarField;
    location    "0";
    object      PsiReal;
}

dimensions      [0 0 0 0 0 0 0];//[0 0 0 1 0 0 0];


internalField   uniform 0.0; 

boundaryField
{
    XMin
    {
        type            zeroGradient;
    }
    XMax
    {
        type            zeroGradient;
    }
    ZMin
    {
        type            empty;
    }
    ZMax
    {
        type            empty;
    }
    YMin
    {
        type            slip;
    }
    YMax
    {
        type            slip;
    }
}

0.orig/PsiImg

FoamFile
{
    version     2.0;
    format      ascii;
    class       volScalarField;
    location    "0";
    object      PsiImg;
}

dimensions      [0 0 0 0 0 0 0];//[0 0 0 1 0 0 0];

internalField   uniform 0.0; 

boundaryField
{
    XMin
    {
        type            zeroGradient;
    }
    XMax
    {
        type            zeroGradient;
    }
    ZMin
    {
        type            empty;
    }
    ZMax
    {
        type            empty;
    }
    YMin
    {
        type            slip;
    }
    YMax
    {
        type            slip;
    }
}

system/controlDict

application     MySchroedingerFoam;//scalarTransportFoam;

startFrom       latestTime;

startTime       0;

stopAt          endTime;

endTime         0.1;

deltaT          1e-6;

writeControl    runTime;//timeStep;

writeInterval   0.001;

purgeWrite      0;

writeFormat     ascii;

writePrecision  6;

writeCompression off;

timeFormat      general;

timePrecision   6;

runTimeModifiable true;

初期状態を作るためにsetFieldsDictを使用します。

system/setFieldsDict

defaultFieldValues
(
    volScalarFieldValue PsiReal 0.0
    //volVectorFieldValue U ( 0.1 0 0 )
);

regions
(
    boxToCell
    {
        box ( 0.3 -1 -1 ) ( 0.7 1 1 );
        fieldValues
        (
            volScalarFieldValue PsiReal 1
        );
    }
);

適当な範囲を$${\psi_{rel}=1}$$にしました。
以下のコマンドで初期状態を作成します。

setFields

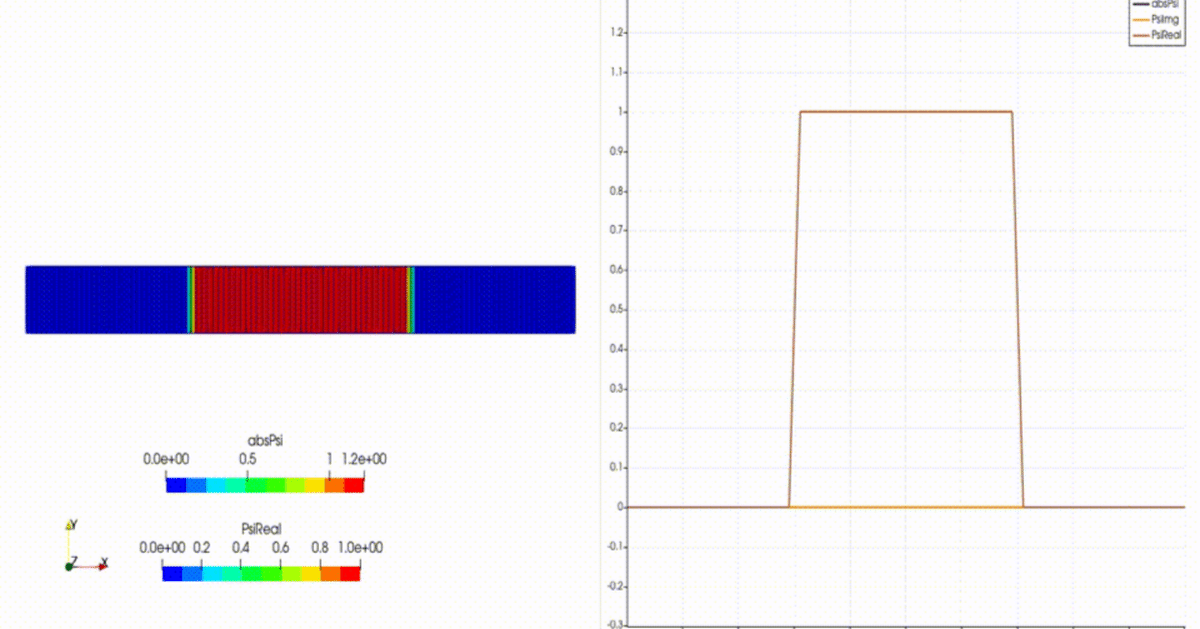
では、計算をさせます。
今回作った新たなソルバを実行します。

MySchroedingerFoam

なにこれ？って感じですが、エラー無く計算できたので良かったです（良くはない・・・）

まずは、ひな形を作るのが大事ですよね・・・・
理論解があるシュレディンガー方程式の問題を設定して、計算の確からしさを検証する必要があります。
色々と今後手直しできればと思います。

まとめ

OpenFOAMでシュレディンガー方程式は解けるのか、少し考えてみました。
laplacianFoamをカスタマイズすれば可能であることがわかりましたが、複素関数を扱うシュレディンガー方程式は少々工夫が必要です。

とりあえず、適当にカスタマイズしてみましたが、「今回は計算ができた」程度のお粗末な内容ですが、今後手直ししていければと思います。

どなたか、興味持った方もやっていただければOpenFOAMも量子力学を扱えるようになる・・・・のかな？と思います。

OpenFOAMによる熱移動と流れの数値解析(第2版)

OpenFOAMライブラリリファレンス

X➡@t_kun_kamakiri
ブログ➡宇宙に入ったカマキリ（物理ブログ）
Youtube➡カマキリ理系ブログ