見出し画像

【2023年5月活動レポート】ブログPV数。その他活動

物理・プログラミング・Python、Web制作・自己啓発

こんにちは。
すっかり熱くなってきたと思ったら、もう今年の半分が終わろうとしていることに気付いた今日この頃。
最近時間が経つの早く感じすぎてマジで恐ろしい・・・

今月も活動レポートを書いていきます。
（前回の活動レポートはこちら）

リヴィさんの活動レポートに便乗して毎月活動記録として残しています。

■自己紹介
・30代半ばの製造業勤務（開発部署でCAE解析）
・大学 理学部物理の修士卒
・ブログ記事月間約5万～9万PV（物理、Python、CAE解析など）
・Twitterフォロワー2277人（2023/6/1)
「宇宙に入ったカマキリ」というブログを運営

現在は工作機械メーカーでCAE解析をしています。
主に流体解析を担当しています。商用のソフトは高価でライセンスが限られているので、無償で使えるOpenFOAMを運用しています。

今気付いたけど、先月から1人もフォロワーが増えていない！
こういう気付きも毎月レポートを書いているからこそですね(´；ω；`)ｳｯ…

ブログPV数

・ブログPV数：92,560PV
・notePV数：2,562PV
・記事数：２記事

今月は記事数を2つしか書けていませんが、PV数は年々伸びていますね🤗
もしかすると今年は6月に10万PV行くかもしれません。

書いたブログ内容

ブログ内容はもっぱら趣味に振り切っているため、役に立つ内容かどうかまったく不明な記事を量産しております。
先月書いていたのはバスケットボール形状に合うように流体解析用のメッシュを作成する方法についてです。

https://takun-physics.net/16125/

OpenFOAMのサポートを出品してみた

最近OpenFOAMばかり勉強しているので、流体解析用のモデル作成のお手伝いしてほしい方いましたらこちらよりお問い合わせください。

モデル作成ではなくエラー内容や学習支援などの要望ありましたら、こちらよりお問い合わせください。

ちなみにこちらのGoogleグループでも質問することができます。有志の方が答えてくれる（かも）しれませんので、お金払いたくないよって方はこちらをご利用ください。

対価が発生するかどうかは目標の達成度合いの違いかと思います。
個別の悩みを高確率で解決したり、ピンポイントであなたに寄り添ってくれるということを希望する方はやはりwin-winという意味でもココナラのサービスからお問い合わせください。

余談ですが、ココナラ手数料高いから自分のブログで宣伝した方がいい気がするけど・・・考え中です。
先月は1件依頼がありました🎉

離散化スキームをプログラム

こちらの質問サービスでよく聞かれる内容をまとめておりました。

ちなみにこちらのサービスは販売実績累計300件を超えています。
たいていの物理の内容（理学、工学）の学部4年生まで習う内容でしたら幅広く対応しております。
※テスト代行などはお断りしております_(._.)_

よく聞かれる内容ってのが離散化スキームの話です。

【概要】
流体の基礎方程式のような偏微分方程式を解く際に、微分を数値的に扱うよう離散化をするのですが、その離散化の方法によって数値解がえらい変わってしまうという問題がある。
そこで1次元移流方程式を用いて有限差分法で移流項の離散化スキームの違いでどのように数値解が変わるのかを検証したい。

商用の流体解析ソフトはいい感じに安定に解くようにデフォルト設定されているようで、CAEポチポチ設定している人には全然興味ない内容かと思いますが、自分は興味があり勉強していました。

ぶっちゃけよく聞かれると言っても、聞かれたのは計3回くらいですが需要があるとみて力入れてまとめてみようと思った次第です。

とにかくいっぱい本を読みました。

有限差分法と有限体積法のTVDスキームという部分の話の流れが両者で違うような気がしてそこで詰まりました・・・・が解決しました。

【ざっくりまとめ】
・有限体積法はセル平均で物理量を定義した保存型のスキーム
・対流項の1次精度は安定であるが数値拡散しやすい
・高次精度スキームは不連続解をシャープにとらえれるが振動しやすい
・1次精度と高次精度の良いところどりをするために流束制限関数で高次の項を調整する

興味がある人にはわかるけど、興味ない人には全くわからない上に役に立たない内容かもしれませんね。

というわけで1次元の移流方程式を色々な離散化スキームでPythonでアニメーションにしてみました。

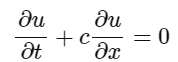
1次元の移流方程式には厳密解が合って、初期状態の形を保ったまま速度cで進行する解が求まります。（絵は速度uになっていますが。速度cと思ってください_(._.)_）

まずは有限差分法でプログラムを書きました。
最も安定ですが数値拡散しやすい1次精度風上差分

2次精度で空間微分の精度は良いが不安定な中心差分

2次精度のQUICK

時間の2次精度、空間の2次精度のLax-Wendroff法

Lax-Wendroff法に流束制限関数を設けて、不連続な数値解では振動しないように抑えつつ、シャープにとらえようとするのが以下のTVD法。

TVD法の中でも強めに高次精度を抑えようとするminmod
安定だがちょっと数値拡散してしまう

TVD法の中でも弱めに高次精度を抑えようとするsuperbee
ちょっと不安定になりがちだが、不連続解ではシャープにとらえようとする

minmodeとsuperbeeの中間くらいで高次の項を抑制するvan Leer

これらの内容を講義ノートとjupyter labにまとめていました。

ひととおり有限差分法はまとまりました。
これで教えてほしいという依頼にバッチリ準備ができた。

次は有限体積法でまとめようと思います。

来月頑張ること

  • OpenFOAM講習会の準備（gnuplotとPython)

  • ChatGPTのAPIとPythonの連携

  • OpenModelicaで振動工学

  • IoTネタをひとつ実践

Twitter➡@t_kun_kamakiri
ブログ➡宇宙に入ったカマキリ（物理ブログ）
Youtube➡カマキリ理系ブログ

いいなと思ったら応援しよう！