見出し画像

OpenModelica勉強(1)

物理・プログラミング・Python、Web制作・自己啓発

こんにちは。
先週よりMONOistの「1Dモデリングの勘所」の連載を読んでおり、1DCAEに再度興味を持ったために勉強を再開しました。

仕事でも使えたらいいなと思っているので本腰を入れて勉強をしていきます。
OpenModelicaの資料は↓こちらによくまとまっているので勉強はしやすいでしょう。

※勉強用メモなので決してわかりやすくは書いておりません。
というか数年前の学び直しです。

Modelicaの概要

システムとは自分たちが知りたい何かしらの特性を持つ対象や対象の集合

  • Modelicaは方程式に基づいている。 非因果的モデリングが可能

  • 複合領域のモデリング能力がある 電気、熱、油圧、機械、生物、制御

  • オブジェクト指向の言語で一般クラスの概念を持っている。 ソフトウェア部品の再利用や改造が可能

  • 部品同士を接続したりして物理量を受け渡すことができる

まずは簡単なところから

OpenModelicaを起動してモデルをModelを作成します。

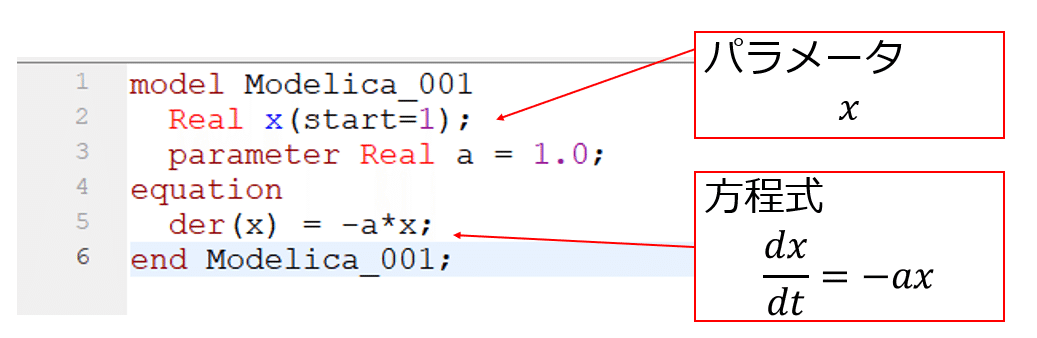
変数の数と方程式の数が一致していると計算実行できる準備が整います。
そして以下のようにシミュレーションの実行をします。

計算が終わったら変数xをプロットします。

質点の振り子の運動

次の例は質点の振り子の問題です。

変数は$${x}$$,$${y}$$,$${v_{x}}$$,$${v_{x}}$$,$${F}$$の5つです。
5つの変数を求めるためには独立な式が5つ必要であるため、以下の5つの式を記述します。

$$
m\frac{dv_{x}}{dt}=-\frac{x}{L}F​\\
m\frac{dv_{y}}{dt}=-\frac{y}{L}F-mg​\\
\dot{x}=v_{x}\\
\dot{y}=v_{y}\\
x^2+y^2=L^2
$$

これをModelica言語で書くと以下のようになります。

model Modelica_002
  constant Real PI = 3.1415926;
  parameter Real m = 1.0, g = 9.81, L = 0.5;
  Real F;
  output Real x(start=0.5), y(start=0.0);
  output Real vx, vy;
equation
  // variable x, y, vx, vy, F  => 5 
  m*der(vx)=-x/L*F;
  m*der(vy)=-y/L*F-m*g;
  der(x) = vx;
  der(y) = vy;
  x^2 + y^2 = L^2;
end Modelica_002;

先ほどと同様に計算を実行すると、以下のように振動した解が得られます。

まとめ

本記事はOpenModelicaの導入部分を自分の勉強メモとしてまとめました。

参考にした書籍はこちらです。

OpenModelicaのモデリカ言語の勉強にはこちらの参考書が良いですね。

最近は日本の書籍も出ているので勉強がしやすいです。

Twitter➡@t_kun_kamakiri
ブログ➡宇宙に入ったカマキリ（物理ブログ）
Youtube➡カマキリ理系ブログ

いいなと思ったら応援しよう！