
Pythonで球体周りの抗力係数のパラメタスタディ
こんにちは('ω')ノ
本日はOpenFOAMでの流体周りの抗力係数を確認してみました。
黒実線が実験値の近似曲線で、青丸が今回のシミュレーションの結果です。
横軸にレイノルズ数と縦軸に抗力係数の常用対数をとったものです。
抗力係数:$${C_{d}=\frac{F_{D}}{\frac{1}{2}\rho U^2A}}$$
レイノルズ数:$${Re=\frac{UL}{\nu}}$$
今のモデルだと高レイノルズ数領域で厳しくなりますね。 https://t.co/MrIWrC6FM2 pic.twitter.com/2nIrm4ZC8I
— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) February 10, 2022
そこそこ試験結果と近しい値をとりました。
全てのレイノルズ数領域で定常解析かつ乱流モデルRANSを用いたので高レイノルズ数領域の再現性が良くありませんね。
より厳密に実機に合わせようとしたら非定常解析かつ乱流モデルもLESなど検討して再付着という現象を再現しなくてはいけないですが、メッシュ数が膨大になり計算時間がノートPCのスペックでは耐えられなさそうなので今は目をつむることにします。
※本記事は決して丁寧な解説を行っておらずメモ感覚で書いております_(._.)_
球体のモデル:FreeCADで作成
球体モデルはFreeCADでさくっと作成してstlファイルで出力します。

メッシュ作成:Xsimを使う
OpenFOAMの解析設定はXsimで行うのが簡単ですね。
Xsim

※Xsimで掃き出されるOpenFOAMがFundation版で、僕が使っているのがESI版v2006なので後ほど色々記述を変える必要があります。
計算実行:球体のまわりの解析実行
Xsimで出力されたフォルダの中にAllrunという名前のスクリプトがあるので実行します。
./Allrun自身が使っているOpenFOAMがESI版だったりgunplotがインストールされていないとメッシュ作成はできても計算が進んでいなかったりします。。。
しかし、今回は./Allrunのスクリプトで計算を実行したいわけではないので、snappyHexMesh後の「constant/polyMesh」を使います。
抗力係数の設定
抗力係数は「orgCase/base_k-epsilon/system/controlDict」のfunctionsで設定します。
FoamFile
{
version 2.0;
format ascii;
class dictionary;
location "system";
object controlDict;
}
application simpleFoam;
startFrom startTime;
startTime 0;
stopAt endTime;
endTime 500;
deltaT 1.0;
adjustTimeStep no;
maxCo 0.9;
writeControl timeStep;
writeInterval 50;
purgeWrite 0;
writeFormat ascii;
writePrecision 6;
writeCompression off;
timeFormat general;
timePrecision 6;
runTimeModifiable yes;
functions
{
forceCoeffs
{
type forceCoeffs;
libs ("libforces.so");
writeControl timeStep;
timeInterval 1;
log no;
patches (sphereMeshed);
rho rhoInf;
rhoInf 1;
liftDir (0 1 0);
dragDir (1 0 0);
CofR (-1.4502967656966168e-05 2.286241662386465e-06 -0.00013135530234728088);
pitchAxis (0 0 1);
magUInf 1.0;
lRef 0.25;
Aref 0.049093946015625;
}
residuals
{
type residuals;
libs ("libutilityFunctionObjects.so");
fields (U p k epsilon);
}
//#includeFunc residuals(U,p,k,epsilon);
#includeFunc yPlus;
#includeFunc CourantNo;
}パラメータスタディ
フォルダ構成を以下のようにしておきます。

orgCaseが元の解析フォルダです。
こちらに先ほどのメッシュデータ「constant/polyMesh」も入れておきます。
orgCaseには色々な乱流モデルで解析ができるようにフォルダを分けておきます。今回は、k-εモデルを使うので「base_k-epsilon」だけを使用します。

orgCase/base_k-epsilonのAllrunには以下の記述を書いておきます。
#!/bin/sh
cd ${0%/*} || exit 1
. $WM_PROJECT_DIR/bin/tools/RunFunctions
decomposePar
mpirun -np 4 pimpleFoam -parallel
reconstructPar
rm -rf ./processor*これで準備ができたのでPythonでパラスタを行います。
pythonのスクリプトを書く
import os
from pathlib import Path
import shutil
import subprocess
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from PyFoam.RunDictionary.ParsedParameterFile import ParsedParameterFile
def clone_file(orgCase, resultDir):
"orgCaseをresultDirに重複しないようにコピー"
baseName = Path(orgCase).name
addName = None
if addName!=None:
baseName += f'_{addName}'
Path(resultDir).mkdir(exist_ok=True, parents=True)
n=0
newCase = Path(resultDir) / f'{baseName}_{n}'
while newCase.is_dir():
n += 1
newCase = Path(resultDir) / f'{baseName}_{n}'
shutil.copytree(orgCase, newCase)
return newCase
#抗力係数の出力
def cd_result(resultDir, newCase):
keys = ['forceCoeffs']
startTime = 0
datfile = 'forceCoeffs.dat'
key = keys[0]
df = pd.DataFrame()
case = str(newCase)
name = os.path.basename(case)
forceFile = f'{resultDir}/{case}/postProcessing/{key}/{startTime}/{datfile}'
df_cd = pd.read_csv(forceFile, sep='\t', header=8,index_col=0)
cd = np.array([ valStr for keys, valStr in df_cd[df_cd.columns[1]].items() ])
return cd
# パラメータスタディ
def new_parameter(newU, newCase):
# 流速の変更
fileU = ParsedParameterFile(newCase / '0/U')
fileU.content['boundaryField']['XMin']['value'] = 'uniform ({:.6f} 0 0)'.format(newU)
fileU.content['internalField'] = 'uniform ({:.6f} 0 0)'.format(newU)
fileU.writeFile()
print(f'Inlet(Xmin) U is now {newU}')
print(f'Inlet(initial) U is now {newU}')
# 抗力係数の代表速度の変更
file_controlDict = ParsedParameterFile(newCase / 'system/controlDict')
file_controlDict.content['functions']['forceCoeffs(sphereMeshed)']['magUInf'] = newU
file_controlDict.writeFile()
# レイノルズ数の計算
def cd_Re(newU, cd):
U = newU
L = 250E-3
mu = 1.511e-05
Re = U*L/mu
# print(f"cd={cd[-1]}")
# print(f"レイノルズ数={round(Re,1)}")
return Re
# 解析実行
def Allrun(newCase):
"Allrunを実行"
out_run = subprocess.check_output(['./Allrun'], cwd=newCase)
return out_run.decode()
# 実験値の近似曲線
def Cd_Re():
Re_ana = np.linspace(0.01, 10000000, 1000000)
cd_ana = 24/Re_ana + ( 2.6*(Re_ana/5) )/(1+(Re_ana)**1.52) + ( 0.411*(Re_ana/263000)**(-7.94) )/(1+(Re_ana/263000)**(-8.00)) +(Re_ana**0.80)/461000
return Re_ana, cd_ana流速を「newU_list = [0.000001,0.00001,0.00002,0.00003, 0.001, 0.01, 0.1, 1.0, 10.0,20.0, 30.0,40.0,100.0]」にしてパラスタします。
以下で連続で実行します。
orgCase = 'orgCase/base_k-epsilon'
resultDir = 'resultDir/'
newU_list = [0.000001,0.00001,0.00002,0.00003, 0.001, 0.01, 0.1, 1.0, 10.0,20.0, 30.0,40.0,100.0]
for newU in newU_list:
newCase = clone_file(orgCase, resultDir)
new_parameter(newU, newCase)
Allrun(newCase)
print('='*50)ひとケース3分くらいの計算時間です。
レイノルズ数と抗力係数を出力します。
レイノルズ数は速度と球体の直径と動粘性係数を計算するだけなので簡単ですが、抗力係数はOpenFOAMの出力結果から取得する必要があります。
from natsort import natsorted
newCase_list = natsorted (os.listdir(resultDir) )
cd_list = []
Re_list = []
for i, newCase in enumerate(newCase_list):
cd = cd_result(resultDir, newCase)
Re = cd_Re(newU_list[i], cd)
cd_list.append(cd[-1])
Re_list.append(Re)Re_ana, cd_ana = Cd_Re()
df_cdRe = pd.DataFrame()
df_cdRe['Re'] = Re_list
df_cdRe['cd'] = cd_list
df_cdRe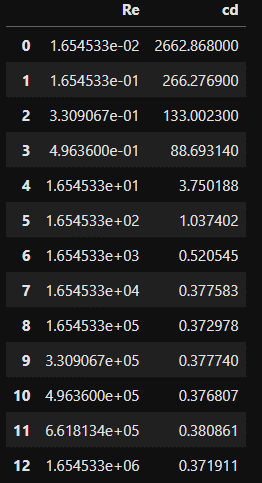
あとはこれをグラフにするだけです。
plt.scatter(np.log10(df_cdRe['Re']), np.log10(df_cdRe['cd']), color='blue', label = 'CAE')
plt.plot(np.log10(Re_ana), np.log10(cd_ana), color='black', label='Exp')
plt.grid()
plt.legend()
plt.xlabel('log10(Re)',fontsize=16)
plt.ylabel('log10(Cd)',fontsize=16)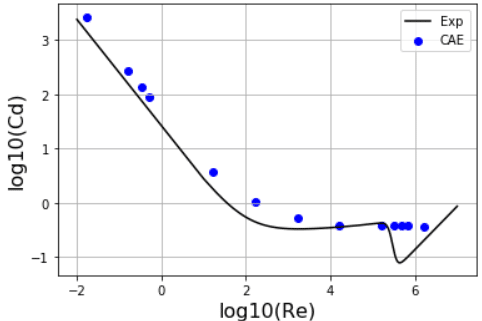
ざっくり説明でした('ω')
参考書
PENGUINさんサイトを体系的に学べる書籍となっています。ネット記事でも十分勉強できるのですが、OpenFOAMの初学者でOpenFOAMをインストール済みであれば一冊持って置き、体系的に学ぶのが良いでしょう。
あとは初心者向けに丁寧に解説がされているこちらの書籍もお勧めです。最後の章にはオーバーセットメッシュ(重合メッシュ)の機能を使った解析を最後まで丁寧に解説しているので挫折することはないでしょう。
Twitter➡@t_kun_kamakiri
Instagram➡kamakiri1225
youtube➡https://www.youtube.com/channel/UCbG6_Q9ZRqqVT6YZOpcjDlQ
ブログ➡宇宙に入ったカマキリ(物理ブログ)
ココナラ➡物理の質問サポートサービス
コミュニティ➡製造業ブロガー
