
5. 概念モデリングに関する圏論的考察 ‐ 議論のとっかかりとして
はじめに
今回は、このマガジンの前の記事や、xtUML 研究会や、ALGAN のイベントで、ちょろっとずつ言及している、概念モデリングへの圏論の適用に関する、途中報告的な記事です。
※ ”圏論(Category Theory)とは”のセクションは、半端な理解の上での中途半端な記述なので、読み飛ばし、最後まで読んでから、戻るという読み方がいいかもしれません。
出発点
圏論(英語では Category Theory)というのは、数学の一分野です。それも相当なレベルの基礎数学の分野。
何故そんなものの習得を試みているかというと、
DX(DT)を標榜する現代のシステム開発において、概念モデリングで説明している様な、開発対象のモデル化は必須だろう
しかし、概念モデリングが実践できる人材は極少数
更に、三十年来の経験から、概念モデリングができる人材を育てるのは至難
特にプログラミングを制御のフローを記述するという考えがしみついている技術屋さんには苦手らしい
ならば、LLM を活用した Open AI 系の AI 技術を使って、関連ドキュメントを入力として概念モデルを自動生成する生成 AI を作った方が早いのでは?
という考えに至りました。
生成 AI の開発に取り掛かる前に、そもそも、概念モデリング、及び、概念モデルというものが何者なのかを、改めてきちんと定義する必要があり、‐ まぁ、”Art of Conceptual Modeling” はかなり厳密に書き込んだつもりではあるのですが ‐ それをしないと、出来上がった AI は”なんちゃって AI”になってしまうのではないかと思ったわけです。
そもそも、
概念モデリングは、システム開発対象の世界からシステム化するために必要な情報を全て洗い出して、モデルとして記述すること
記述されたモデルは、システムに関連するステークフォルダー間で共有される
記述されたモデルは、変換による実装により、コンピュータ上で実際に稼働するソフトウェア一式に変換可能
であり、改めてのきちんとした定義を行うには、
出来上がったモデル = そのモデルの作成者が対象世界をどう認識したか
モデリング体系 = 数学的な観点による厳密な定義
モデル記述に関する標準的な記法 ⇒ UML(Unified Modeling Language)
が必要だと考えています。最初の項目は、認識論が絡む哲学だよね、という事で、フッサールの現象学で基礎づけられるというのが私の現時点の見解です。詳しくは、
「3. モデリングとは ~ 現象学からの考察|Knowledge & Experience (note.com)」
に詳しくまとめたので読んでみてください。
一つ飛ばして、3番目の項目は、既に Unified Modeling Language(ISO/IEC19505)が国際標準なので、それで良いだろうと。
個人的には、システム、要求、現実世界、プログラムコード、全てを一つの記法で描くことが、果たして良いのかはちょっと疑問なんですけどね。モデリングに関する一般的な誤解を再生産し、概念モデリングの理解を妨げる要因の一つなんじゃないかなと。
まぁ、それはそれとして、四半世紀前、多くの方法論提唱者たちが鎬を削りながら、UML という標準記法が提案されていく様を、私は、非主流派側から眺めていました。その頃のことは、また別の機会に色々と書いてみようと思ってます。
で、二番目の”数学的な観点による厳密な定義”については、数学基礎論の一種の、今回の主題である、圏論(Category Theory)を適用すると上手くいくのでは、ということで、雑務の傍ら、勉強を続けているわけです。
きっかけは、新宿ピカデリーに”ベイビーわるきゅーれ 2ベイビー”を観に行った帰り道、コクーンタワーの Book 1st に立ち寄った事でした。
”みんなの圏論”、”活躍する圏論”を書棚で見かけて、パラ見した時に、「これだ!」と思った次第。
それまでは、漠然と、「モデリングを基礎付けるのは”集合論”かなぁ…」と思いながら、でも、なんとなくしっくりこない、という感覚でいました。”圏論”という言葉自体は、これまでどこかで聞いた気もしていたのですが、改めて、既存の数学体系では、”集合論”の基礎付けも可能な”圏論”が、誰が何と言っても最適なのは間違いないでしょう。(多分)
圏論(Category Theory)とは
2023/4 から9月半ばまでに結構沢山の圏論関係の本を購読しました。
しかし、未だに、基本的な部分しか理解していない、というか、理解したと思っている項目も、恥ずかしながら、本当に理解をしているか確信が持てない状況というのが本当のところなので、大上段から「圏論っていうのはね」というレベルにはありません。
※ 多分、講演する時は、自信もって「圏論っていうのはね…」と言いそうですが…その時はクスっと笑って流してください。
現時点までに通読した本を参考までにリスト化しておきますね。
読んだ本リスト
2021/12/10 ‐ David I. Splivak 著・川辺 治之 訳
2023/2/25 - Brendan Fong 著・David I. Splivak 著・川辺 治之 訳
2022/10/22 - 西郷甲矢人、能美十三 著
圏論の歩き方委員会 編
2020/1/30 - 蓮尾一郎、鈴木咲衣、葉廣和夫、長谷川真人、小嶋泉、西郷甲矢人、丸山善宏、阿部弘樹、中岡宏行、土岡俊介、春名太一
2019/12/15 ‐ 西郷甲矢人、田口茂 著
2023/1/10 ‐ 西郷甲矢人、中澤俊彦、松森至宏 著
2022/5/16 ‐ 西郷甲矢人、能美十三 著
線型代数対話 第二巻 モノイドの線型代数 モノイダル構造から行列計算へ
2022/3/22 ‐ 西郷甲矢人、能美十三 著
1994/6/7 - 横内寛文 著
線型代数対話 第三巻 量系のテンソル積 多重線型性とその周辺
2023/5/22 ‐ 西郷甲矢人、能美十三 著
1971/3/27(原著:初版の序)Saunders Mac Lane 著、三好博之、高木理 訳
2020/9/20 ‐ 雪田修一 著
振り返れば、最近流行りの、LLM の学習みたいな感じで、私の頭の中のニューラルネットを学習させた感じかなと。用語を問われれば、「それはこんな定義だよ」という事は答えられますが、それがどんな意味で、それだから何なのというのが今一つピンと来ていない状況です。
なんかさぁ…久しぶりに”わかんねぇ…”という感覚。
小・中学校で算数・数学が分からない生徒達の気持ちってこんなもんですかねぇ…
勝手な想像で恐縮ですが、算数・数学で嵌まるのが、
‐ 具体的な1個、2個、…やひとつ、ふたつ、…が、抽象的な 1、2、…になる
‐ 変数 x とか y とか、ある値域に属する値を持つものの登場
‐ 関数
あたりかなと。実はこれら全部、圏論を使うと全部、ちゃんと数学的に定義できる…
圏の定義
さて、本題の圏論ですが、基礎的な概念として、圏、関手、自然変換、随伴、普遍性、ユニバース、…、等が出てきます。
先ず、圏(Category)の定義ですが、実はこれに対する理解についても、ちょっと手間取ったんですよ。書籍(の書き方)によって定義の仕方が微妙に違うんですね。幾つかピックアップしてみます。
まずは、”圏論の道案内”から

う~ん。。。これ、凄く工夫していると思うんですよ…
しかし、著者の方、ごめんなさい。ほぅなるほど…とはいきませんでした。判らない理由は
A や B が、対象の全体なのか、個別の対象なのか曖昧
f や g が対象夫々に対するものなのか、良く判らない
D や X、Y という説明のない記号がいきなり図に出てくる
射、その域、余域、合成等の書き方が複数ある
あたりによります。特に、概念モデリングでは、個別の概念インスタンスと、その分類である概念クラスというスキーマが頭に沁みついているので、この辺がはっきりしないとすごく気持ち悪い。
次は、”圏論の歩き方”

これで、”圏論の道案内”での疑問が解消されました。しかし、”圏論の歩き方” 第一章のこの定義の後にも書いてあるように、「これではわからんわけですよ」で、その後に続く文章で、圏論とは何かを補足(”圏論の道案内”でももちろん、懇切丁寧に補足をしてますよ)していて、理解の助けにはなりました。
他の、”みんなの圏論”、”圏論の基礎”等も、説明の仕方は異なれど、要するに
対象(何でもよい)の集まりがあって、ある対象をある対象(対象は同じ対象でも可)に移す射が存在(射はその始点になる対象:域とその終点になる対象:余域がひとつづつある。こう書くと域と余域に紐づいた射は一つだけの様な印象を抱くかもしれないが域と余域のペアに紐づく射は複数あってよい)し、全ての対象は、各対象自身に移す恒等射をただ一つだけ(域と余域が一致する場合は射は一つだけだといっている)持っている。つまり、それぞれの対象とそれぞれの恒等射は一対一対応し、各対象を区別(Identityなんだからそう考えて良いだろう)可能である。
ある対象をある対象に移す射 f の余域(終点:cod(f))と別の射 g があり、射 g の域(始点:dom(g))が同じ、つまり、cod(f)=dom(g)で、射 g の余域(終点:cod(g))がある場合、合成された射 g◦f が一つだけ存在する。
更に、3つの射、f,g,h: cod(f)=dom(g) かつ cod(g)=dom(h) が存在する場合は、dom(f) の対象に、f と g の合成された射 g◦f を適用して得られた対象(cod(g) に等しい)に、h を適用した結果得られた余域と、dom(f) の対象に f を適用して得られた対象(cod(f)に等しい)た後に、g と h の合成された射 h◦g を適用して得られた対象(cod(f)=dom(h◦g) の cod(h◦g))が等しくなければならない(結合律)、つまり、h◦(g◦f) = (h◦g)◦f がなりたつ。
(個人的には以上の定義で自明なんじゃない?とは思うが)f:X→Y なる任意の射 f に対して、域を f で写した後に、その余域の対象の恒等射を適用した結果と、域の恒等射をまず適用して得られた余域を f の域にして写した結果は一致する。
加えて(”圏論の道案内”定義2.6より)、f:X→Y なる射 f と g:Y→X なる射 g があり、g◦f (※ 対象 X に f を適用した Y にgを適用する)が X の恒等射と等しく(※結果的に最初の対象Xに戻る)、かつ、f◦g が Y の恒等射と等しい(※ 対象 Y に g を適用した X に f を適用して得られた Y が最初の対象 Yと一致する)場合、g を f の逆射と呼び、逆射を持つ f は、可逆であるといい、可逆な射を同型射という。同型射を持つ X と Y は一対一対応が可能なので、X と Y は同型であるといい、X≌Yで表す。
を満たすものが、”圏”だよ、という事のようです。定義の中で図による表現が出てきますが、矢印で表される射(始点が域、終点が余域、射は複数の射の合成でもよい)を複数書き込んで、対象間、射間を図で表す図式は、それぞれの射の可換性を示しています。
以上の基本的な定義の上に、様々な構造を構築して、色々な論理や概念を定義したり、性質を調べたりする、それが圏論という事になります。
集合と何が違うの?
「対象の集まり」と聞くと、「それって集合じゃないの?」と思う方、多いと思います。確かに昔々は、”集合=物の集まり”という素朴な定義の時代があったのですが、有名な「ラッセルのパラドックス」(※これ、初出が1902年!実に100年以上前の話なのね)が発見されて、”集合=物の集まり”という素朴な定義では集合の集合とか無限集合とかで色々と問題が出てしまうんですね。なので、「集合って何?」とか「集合の要素(物)って何?」というのを定義しなければならなくなったわけですね。Wikipedia の「ラッセルのパラドックス」のページには、”矛盾の解消”で3つの解決方法が紹介されていて、圏論による解決方法は書かれていませんが、集合という概念を持ち出す以前の、”何でもいいから対象” と ”その対象間の関係”から公理を構成しようぜ、というのが”圏論”という事らしいです。もちろん圏論は集合論を包含するので、圏論で集合を再定義した”集合圏”なんてのもあります。昔々は集合論が数学の基盤だったので、圏論は、数学の基盤を定義する基本的な概念という事も言えそうです。
集合の場合は、”集合の集合”とかを素朴に考え出すと矛盾が出てくるのですが、単に”対象はなんでもよい”という圏論は、なんでもよいので、”圏”や”射”、更には、”圏”や”射”から派生する”関手”(後述)も”対象”として扱う事が出来ます。
また、集合論は、その要素が主眼に置かれていて、写像等は派生的な扱いであるのに対し、圏論は、要素(対象)だけでなく、対象間の操作的な射も対等に扱っているのも特徴です。私が読んだ書籍の多くの著者が、対象よりむしろ射の方が本質ではないかとも思っている感じです。
概念モデリングと圏論の相性は良い(多分)
概念モデリングは、(多分間違ってないと思うけどあまり自信がないw)モデル化対象の世界(現実世界だったりソフトウェアだったり)に存在する様々なモノ・コトを抽出してモデル上の要素群に移す事であり、”現実世界の様々なモノ・コト”や、”モデル上の要素群”を、”圏の対象”、写す事を”射”と考えることが出来ることになり、モデリングという行為は”射”を実行する事とも考えられますよね。更には、概念情報モデルなんかは、それ自体が対象と射からなる圏だろうし、変換による実装の基本的な道具立てである”メタモデル”等も圏として扱えるんだろうなというのが現段階での私の感触です。
対象より射を重視する考え方は、概念情報モデルの「”概念クラス”も大事だが、”Relationship”はもっと大事」という事にも通じるように思えています。
圏の基本的な紹介は終わりましたが、これだけだと使い物にはならないし、単なる圏の説明にすぎず圏論の説明になっていないので、概念モデリングにおける圏論の活用方法は後述することにして、圏の定義を元にした、圏論で知っておかなければならない必須の概念を説明してくことにします。
集合と関数の圏:Sets
集合(と関数)を圏論で定義すると、

だそうです。”関数”は、一般的な集合論では、集合間の”写像”と同義だと思ってください。”圏論の道案内”第7章にもある通り、また、各書、説明がそれぞれ違い、集合圏(集合圏自体が色々ありそう)に関する厳密な定義があるようですが、ポイントは、少なくとも「ある要素がある集合の要素かどうか判断できる」という点で、”判断できる”=射 で、集合とは何かを、集合の要素を元に定義するのではなく、射を使って定義するというのが、圏論の流儀だそうです。
関数は中学の算数で習う”関数”と同じなので、x ∊X(x は集合 X の要素だよってこと)に対して、関数を f とすると、f(x) = y(f:X→Y という書き方と同義) 、つまり、要素 x に関数 f を適用した結果、写される先の y が必ず1つ存在するという事を意味します。y は y ∊ Y(y は集合 Y の要素)で、X と Y は同じ集合でもいいし、異なる集合でも構いません。
このとき、x1,x2∊X 、つまり、x1、x2 は X の要素で、かつ、異なる要素に対する関数 f の写し先(集合 Y の要素のうち位のどれか一つ)が同じでも異なっていても、関数の定義としては問題ありません。また、集合 Y の要素の中で、関数 f の写し先にはなっていない要素があっても、関数の定義としては問題ないです。
x1, x2 ∊ X で、x1、x2 が異なる要素の時、それぞれの関数 f の写し先が異なる場合、つまり、x1≠x2の時に、f(x1)≠f(x2) なら、その関数を、単射(injection)と呼びます。
また、y∊Y、つまり、集合 Y の要素全てに、関数 f によって写される x∊X が存在する場合は、その関数を、全射(surjection)と呼びます。
更に、関数 f が、単射、かつ、全射の場合は、その関数を、全単射(bijection)と呼びます。全単射の関数は、X の要素と Y の要素が一対一に対応することになるので、x = g(y) とすると、X の要素に対して f を適用した結果(Y の要素)に、更に、関数 g を適用すると、元の X の要素に戻ることになります。結果として、f が全単射の場合、g という逆関数(inverse)が存在するという事と同義になります。ある二つの集合 A、B に対して全単射の関数 f がある場合、集合の要素の数は等しく対等であるという事になります。これは、要素を一つ、二つ、三つと数え上げるという行為の基礎になります。また、a1,a2∊A(a1、a2は集合 A の任意の要素) について以下の条件の 1~3 を満たすとき、要素が前順序関係(preorder relation)であるといい、(要素に対して)前順序関係が定まった集合を前順序集合(preorder set)と言います。
どんな a1,a2 に対しても a1≤a2 であるか、そうでないかが決まる
a1≤a1
a1≤a2 かつ a2≤a3 ならば a1≤a3
a1≤a2 かつ a2≤a1 ならば a1=a2
どんな a1,a2 に対しても a1≤a2 であるか a2≤a1 であるかが成り立つ
上の条件1 を見るとなんとなく要素が数字に思えてしまいますが、数の集合に限定しているわけではないので、例えば、A が動物の集合で、a1が犬、a2 が猫だとすると、”≤” は意味がありません。”a1≤a2である”を圏論風に、”a1→a2”と読み変えると立派な射に対応し、上の条件3は、圏の定義に出てきた合成であるといえます。条件2 は圏の定義で出てきた、恒等射があるよという事らしい。
集合の二つの要素の間の関係が条件1を満たすとき、これを2項関係(binary relation)と呼ぶそうです。
更に、1~4 までを満たす場合(圏論の道案内P42では、”…をみたすものは”と書かれているが、ものという言葉を使われてしまうと文脈的に混乱してしまうのでここでは場合に置き換えています)は、半順序関係(partial order)、そして、1~5までを満たす場合は、全順序(total order)と呼ばれるそうです。
条件2 を見て、何故、”=”じゃなくて”≤”なんだろうと思いませんか?
最初に”順序”って書いてあるので、なんとなく”≤”が数字の大小を表している様に思えてしまうのは私だけでしょうか?文面には、”≤”が大小関係を意味するなんで音はどこにも書いてないんですね。単に”≤”という記号を使っているだけで、別にこれは、”☆”でも”⦿”でも何でもいいんです。そういう記号で結びつけられた二つの要素、言い換えれば、射を使って、”順序”とはこういうものだという定義を行っているというのが正解。”=" というのも同じ(多分)なので別の記号、例えば”≠”、”≂”を使っても全然かまわないと。条件2の段階では、”=” の意味的な定義が成されてない(多分)ので、条件1で定義された”≤”を使っているんだと思う。(ほんとか?)
”=”の意味は、条件4 で、条件1~3 までで規定された”≤”を使って定義された、と考える方がいいんですかねぇ…
深読みが過ぎるか?
そんな流れで、”犬(a1)と猫(a2)の場合は≤に意味はない”を読んだとき、”犬が猫より好きって解釈できるんじゃないの?”と思った人、いませんか?
はい、それはそれで、多分、正しいんだと思います。
先ず、a1、a2 として、犬、猫という要素が妥当かどうか、つまり、考えている集合 A が”哺乳類”という集合(”ネコ目”という集合でも、”脊椎動物”でも可)だということですね。ここでは、ある対象(生き物でなくても可)がその集合の要素なのか否かが、明確に判断できる基準があるよと、いう事です。で、その判断に従って、様々な対象を取り上げて集合 A の要素とし、二つの組を作って、どっちが好きかを決める、あるいは、決めないを全ての二つの組に対して決めれば、それは前順序集合だという事になります。
で、そういうどっちが好きか(好き嫌いと言わないところが味噌w、好きの反対は嫌いじゃないという事ではなく、ここでの”≤”は、二つの要素のうち、どちらがより好きか、ということなので)という集合(圏と言っても良い)が定義されたという事になります。
更に言うと、こういう好きの前順序関係が定義された集合と、全順序関係が定義されていない単なる(まぁ、これも定義次第なんだが)哺乳類の集合は同時に存在しても良いし、同じ犬が両方の集合の要素になっていても全然かまわないんですね。同じ犬が両方の集合の要素になっているという事は、二つの集合の間に何らかの関係性があるという事になって、それを記述するのにも圏論が使えるらしい。
ちなみに、”みんなの圏論”では、前順序は、擬順序という名前で紹介されています。順序は、単なる大小関係ではなく、時の通り、一列に並んでいるとか、グラフのアローのつながりとか、様々な構造の基礎になるので、諄く書いてみた次第。
モノイド(Monoid)
さて、次は、”モノイド(Monoid)”です。”圏論の道案内”によれば、
定義2.7
対象がただ一つの圏をモノイド(monoid)と呼ぶ
う~む…良く判らない…というのが正直な感想です。”対象がただ一つ”ってのが私にとっては意味不明なんですね。でもこの節をよくよく読むと、
…対象を自然数全体N、射としては自然数同士の対応を考えてみよう…
と書いてある(更にN は中抜きの字体で書いてあるので個々の要素ではない)のと、集合の前順序関係の後に続いて書いてあるので、定義2.7 の”対象”とは集合の事なんだと納得。他の書籍でも、モノイドは集合であることが前提になっているようなので、多分、正解。要するに、
射の域と余域が同じ集合 = モノイド
ってこと。対象の集合は一個でも射(集合の要素間の話)は複数ある事に注意。”圏論の道案内”は平易な言葉で会話形式で詳しく解説されていてとても良いのですが、ところどころ言葉の使い方が雑なので、その辺りを改良した版を出してくれるとありがたいですね。。。
数学で有名な概念との関係として、任意の射が可逆なモノイドを群(group)と呼んだり、逆に、モノイドではない(対象が同じ集合ではない)圏で任意の射が可逆なものは、亜群(groupoid)と呼ぶらしい。
話をモノイドに戻すと、”圏論の道案内”では、第二章の⑦が”モノイドと群”、⑧が集合圏、で、次の⑨が”モノイドの圏”と説明が続きます。お、ってことは⑦は、圏の話ではないんですね。今気がつきました(苦笑)。
”圏論の道案内”の定義2.10はモノイド準同型の定義のお話で、”圏論の歩き方”の定義2.10 はモノイドの定義に関するものらしいですが、内容を比較すると同じ事を言っているようなのでので、後者で書き下ろす(判りやすくちょっとづつ追書き)と、
モノイド(圏)とは、次のような3つ組 (X,・,e) のことをいう。
- X は集合
- ・X×X → X は X 上の二項演算(乗算)
- e∊x は X の元(単位元)
ただし、・と e は次の規則を満たしていなければならない。
- [結合律] x・(y・z) = (x・y)・z
- [単位律] e・x = x = x・e
う~ん。やっぱりちょっと違うか。”圏論の歩き方”風に、”圏論の道案内”の定義2.10を書き下す(こちらも少し追記)と
モノイド M の合成を・、単位元を e と現わし演算・を備えた射の集合と同一視する。また、射の集合を再び M として、<M,・,e> と表すことにする。集合としての写像 f:M→N がモノイド準同型(monoid morphism)であるとは、
※ M、N はそれぞれ別のモノイド
※ f は、Mの要素を N の要素に写す
※ M は <M,・,e> で表し、N は <N,◦,i> で表すことにする
- M の任意の要素 a,b について
f(a・b) = f(a)◦f(b)
- f(e) = i
が成り立つときにいう
あ、全然違いましたね。どちらにしろ、ここで、”演算”という概念が出てきます。”演算”って何?「そんなことも判らないの?」と言われそうですが、”圏論として演算をどう定義しているのか”という事なんですね。つまりは圏論は、”対象”と”射”を元に構築される論理体系なんだから、”演算”もちゃんと、対象と射で定義されるべきでしょう、という事です。
どの書籍にも残念ながら、説明がありません。
圏論的に言うと、
ある対象の集まり X(ここでは集合でなくても良いとしますね)の任意の二つの対象(同じでも異なっていても良いとしましょう)を x1,x2 を選び、その二つの組を域とし、ある対象 y (y は X に属していても、別の対象の集まりに属していても良い)を余域とする射
ってことですかね?y が X に属していれば、モノイド上の演算?
だとすると、域は、3つ以上でもいいんじゃない?とか色々と疑問が湧きます。※ 概念情報モデルの Relationship の両端の多重度を意図的に変える癖のせい(苦笑)
圏論の専門家の諸先生方、教えてください。
まぁ、要するに数の足し算、掛け算の様に、演算は、結合・交換できるよ、という事と、二つの集合があって、それぞれの要素を一対一対応させる射(つまり全単射)がある場合は、演算(写される側で定義された演算)してから f を適用した結果と、f で写してから演算(写された側で定義された演算)した結果は同じだよという事。この事実は案外重要で、そういう関係にある二つの集合(モノイド準同型)があった時、片方の集合で何らかの証明が成されれば、もう一方の集合でも成り立つよ、って事。数学では、幾何学の問題を代数的に解いたりするけど、正にそれ(らしい)。
いずれにせよ、モノイドは、色々な議論を展開する上で土台になるようなので、ちゃんとした理解が必要なようですね。多分、概念情報モデル上の Relationship 定義や Traverse、概念クラスと特徴値、等々、モノイドなんだろうなという予感。
関手
前にも書いていますが、圏の対象は「何でもよい」ので、圏も対象となり得ます。圏(異なっていても同じでもよい)の構造を保つ射的なものを関手(functor)といいます。実際に圏論を使って、様々な複雑な事(複数の圏が存在する様な世界)を語るための基本的な武器ですね。

圏の”射”は、圏の”対象”間をものでしたが、関手は、対象を”圏”とし、”圏”の間を写す(正確か?)ってことですね。圏は、対象と射からなるので、当然写す対象(紛らわしい…苦笑)は、圏の”対象”と”射”になるっす。
判り難いので書き下すと、
最初の条件は、
圏 C の射 f に対して、射 f の域(x)、余域(y)を、圏 D の対象に写す(変換する?)ことができて、かつ、射 f の域を写した圏 D 上の対象(F(x))を域とし、射 f の余域を写した圏 D 上の対象(F(y))を余域とする射(F(f))が、圏 D 上の射として存在する
で、いいのかな?二番目の条件は、
圏 C 上で定義された二つの射(f,g)がある場合、圏 C 上で、ある対象(c)に対して、 f、gの順に射を適用した結果を関手 F で写した圏 D 上の対象(x)と、圏 C 上の対象(cと同じ)を、関手 F で圏 D 上の対象(d)に写し、その対象 d に対して、圏 F の射(f,g)を関手 F で写した圏 D 上の射(F(f), F(g))を使って、F(f)、F(g) の順に射を適用した結果は、xと一致する
モノイド準同型の時と一緒で、圏内の射の適用と関手による圏間の適用の順序は交換可能だよってことですね。
で、三番目の条件は、
圏 C 上のそれぞれの対象に紐づいた恒等射について、関手 F を通じて対応する(写された)圏 D 上の恒等射がただ一つ存在する。論理的帰結として、その圏 D 上の恒等射は、その対象(圏C)を関手 F で写した圏 D 上の対象に紐づいた恒等射と同じ。
ってこと。これらの条件を満たす関手があれば、(本来なら説明に”全ての”とか”任意の”という枕詞がついているといいんだけどね…複数の書籍の説明をチェックすると、圏 C 側の対象、射は、”全ての”とつけても大丈夫らしい)、圏 C の任意の対象に対する圏 D のいずれかの対象と、圏 C の任意の射に対応する圏 D のいずれかの射が存在する事が保証され、更に、圏 C 上の対象に対する射の適用結果は、関手によって圏 D 上に対応付けられるという事になる訳ですね。
この辺、”圏論の歩き方”第七章 P113 定理7.1 に同様な事が書いているので、間違いないでしょう。
これ、圏C = 現実世界、圏D = 概念モデルと読み変えると、関手 F = 概念モデリング ってことになるんでしょうかね。
なんとなく判ったような判らないような…
概念インスタンスの集合と、概念情報モデルとの関係っぽいので、”圏論の道案内”で紹介されている有向グラフを例にした関手の説明を参考までに紹介しておきます。

うぅ…すいません。一瞬理解したような気がしたのですが、どう等しいのかわからない。。。。
ん?まてよ。関手の定義の最初の
「圏C の射 f:X→Y を、圏D の射 F(f):F(X)→F(Y) に対応させる」
というのは、単に対応させる、という事なんですかね。この場合、圏 C = DiGraph、圏D = 具体的な有向グラフ になるので、具体的な有向グラフの各写像毎(定義から同型射ですねそういえば)に、対応関係を考えていく…でいいのかしら…
もうちょっと考えてみますね。
自然変換
次は、自然変換です。関手は射の構造を保つのに対し、自然変換は関手の構造を保つことだそうです。
関手の理解もまだ曖昧なのに、続けていいんだろうかと思いつつ…
ここでは、”圏論の道案内”の第四章の説明を紹介しておきます。
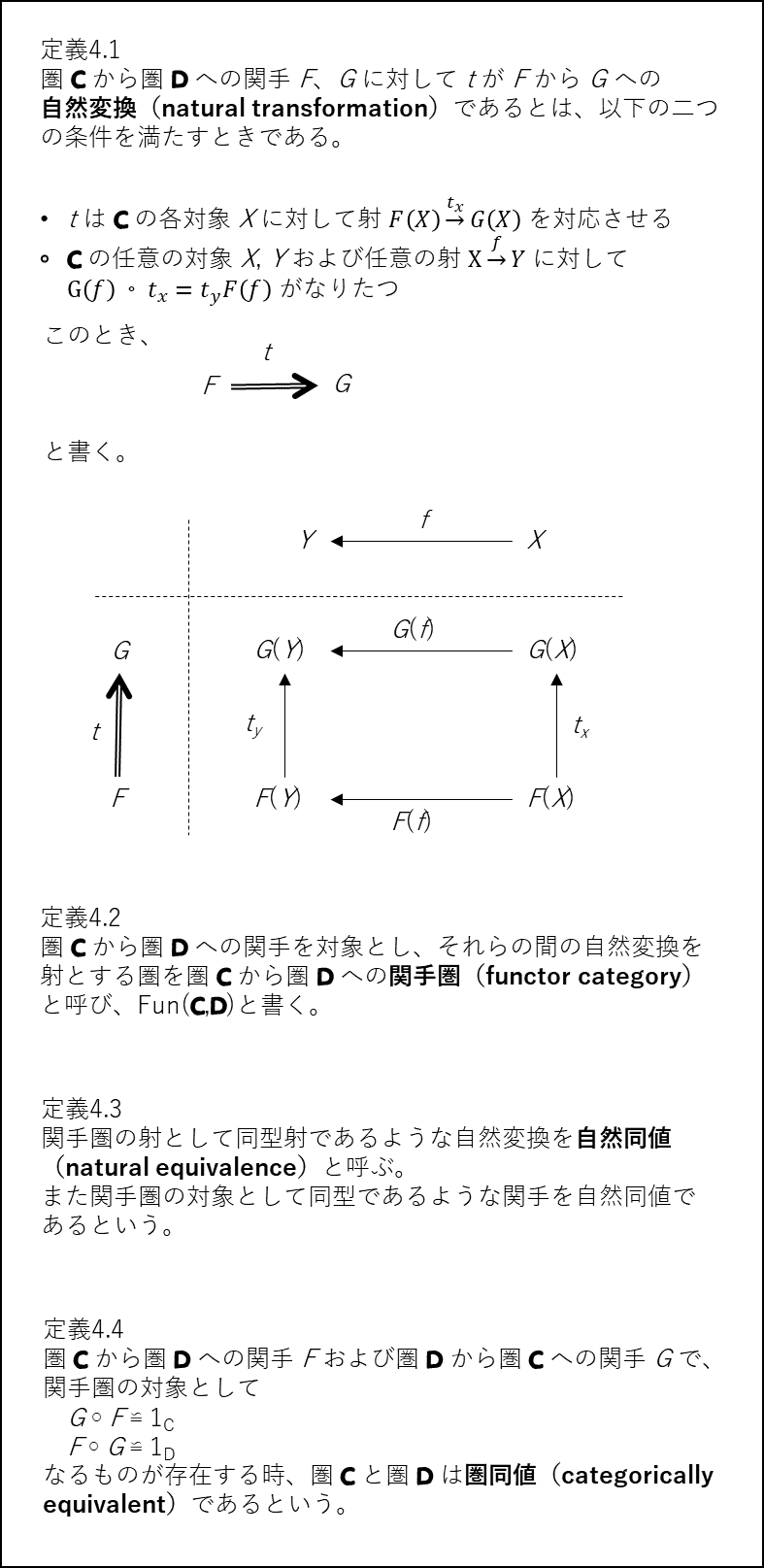
そもそも、関手というのは、「表現」、「モデル」、「理論」、あるいは、「喩え」と同等のものだそうです。物事の記述が”圏”であり、記述は表現事、あるいはモデル化の方法毎に変りうるし、更にはものごとそのものも”圏”のはずなので、圏と圏を対応付ける関手が、「表現」、「モデル」、「理論」、あるいは、「喩え」であるというのには、個人的にはしっくりくる話です。
この辺り、”圏論の道案内”の第7章でも詳しく書いているので、参考になります。
自然同値、圏同値、どちらも、異なる二つの対象世界の本質的な同じさを記述するものですが、自然同値は関手の話なので、「一見そうは見えないかもしれないが、本質的にやっている事が同じ」という事だそうです。世の中ではやり方でもめるケースが結構ありますが、それぞれのやり方を圏として定義して、自然同値かどうかを確認すれば、本質は一緒だね…と笑えるんでしょうね。
一方、圏同値は、圏の「骨組み」の同一性を言っているらしい。一見そうは見えないが骨組みが一緒の二つの対象があり、その間を取り持つ関手が自然同値ならば、どちらの圏でやっても結果は一緒、あるいは、片方の圏で出来ることは、別の圏でも出来る、という意味になるようです。
私自身は、まだちゃんと理解できているレベルには無いのですが、自然変換、米田の補題、単位系の話あたりは、概念モデリングや変換による実装の妥当性に関する様々な知見が得られそうです。
他にも、hom関手、ホモロジー、離散圏、終対象、始対象、同型を除いて一意、積、余積、冪、一般圏、極限、余極限、普遍性、双対、CCC、モナド、トポス、選択公理、随伴、ユニバース。。。圏論を使いこなすために理解しないといけない基本的な要素がまだまだ残っていますが。。。
概念モデリングの基本的な考察をするには十分な材料がそろったと思うので、この辺で説明は止めることにします。
ここまで、ちゃんと全部読んできた読者は皆無だと思いますが、もしいたら、お疲れ様でした。
圏論から見た、モデル化対象世界(現実世界)と概念モデリングの関係
さて、長々と圏論の基礎的な概念を、私の理解の進捗と共に書いてきましたが、ここからは、Art of Conceptual Modeling で説明している概念モデリングについて、圏論から見た基礎的な考察を書いていく事にします。
圏論の応用については、以下の二つの観点から考えていく事にします。
現実世界の写しとしてのモデル
概念モデリングは、理解し、記述したい世界をモデル化する技術であると、様々な場所で再三再四書いたり話したりしてきています。あるビジネスシステムを開発するとしましょう。その際、開発対象のビジネスの内容(世界)を正確に理解せずにそのシステムを開発できるでしょうか。答えは当然のことながら否です。
システム開発に限らず、業務でタスクを完遂するにしても、日常でも何かを成し遂げたい場合も、少なくとも、その対象となる世界を理解する事が必要なのは間違いないでしょう。システム開発や業務のタスク遂行は、複数人が関与し、その人たちの理解も必要になるので、理解するだけでなく、どう理解したかを適切な観点から記述し、共有しなければなりません。
さて、世界をモデル化するという事を圏論的に考えてみます。
理解したい観点から眺めると、モデル化対象となる世界には、複雑に絡み合った様々なモノやコトが存在しています。先ずは、それらの、モノ、コト、モノやコトの間の関係、全てを、圏論の定義に出てきた用語でいうところの、”対象(Object)”と考えるができます。
※ このセクションでは、”対象”という言葉は、”モデル化対象”の様な形で既に使われていて紛らわしいので、これから以降、”オブジェクト”と書くことにします。ソフト屋さんが”オブジェクト”という言葉を聞くと、直ぐに、”オブジェクト指向プログラミング”を思い浮かべてしまうかもしれませんが、全く関係ないので、一旦、”オブジェクト指向プログラミング”の事は忘れてください。
対象世界を構成するモノやコトが、理解したい観点において持っている意味的な関係を、圏論の定義に出てきた用語でいうところの、”射(morphism)”であると考えることができるでしょう。モデル作成者が理解したい観点が明確な場合、この射は、圏論の定義で出てきた、射の合成と結合律が成り立つはずです。
もし成り立たないなら、それは、モデル化しようとしている対象世界、あるいは、理解したい観点が混乱していて、必要以上に発散している事を意味するものとします。経験上、この様な状況では適切なモデルは作成できないので、モデル化対象を見直して分割したり、理解したい観点の見直しや整理が必要です。
射の合成、結合律が成り立つのと同様、対象世界を構成するあれやこれ(全てオブジェクト)はそれぞれを区別できるはずです。これは、圏論の定義で出てきた用語でいうところの、恒等射です。
以上から、モデル化対象の世界は圏であると考えられることになります。この圏を 圏 W と呼ぶことにします。
※ 圏の対象(Object)は、何でもよいので融通が利いていいですね。
一方で、対象世界のモデルは、圏であるとします。数学的にきちんとした基盤を持つモデリング技法であれば、出来上がったモデルは当然、圏になるはずです。この圏を 圏 M と呼ぶことにします。

これで準備が整いました。対象世界が正しくモデル化されているという事を圏論の用語で書くと、
圏 W と圏 M が自然同値(natural equivalence)である
という事になります。(多分それで間違ってはいないと思う)
一応断っておくと、自然同値を可能にするモデリング体系に従ってモデル(圏 M)を記述し定義したからと言って、自然(自動的)に 圏 W と 圏 M が同値になるという意味ではありません。逆に、
圏 W と 圏 M が同値になるように、モデルを記述しなければならない
という、あくまでも、モデリングに対する要請であり、指針であると考えなければなりません。逆に言えば、この要請があるので、作成したモデルの正しさは、圏 W 側のオブジェクトを拾い上げていって、圏 M 側のモデルに対応するオブジェクトがあるかを対応付けていく事によって検証可能になります。
以上を踏まえての話ですが、圏 W と 圏 M が同値であるという事は、圏 W 上のオブジェクトをあまねく拾い出して 圏 M のモデルを作り上げていく事を意味します。実際、”Technique of Transformation” で解説している”変換による実装”を活用する場合は、そのようなモデルの作成が要請されます。後述の、”Art of Conceptual Modeling”のモデリング体系は、そのようなモデルを作成する為のものです。
しかし、”変換による実装”を使わない場合、例えば、概要やスケッチレベルのモデルで十分な場合は、自然同値を求めるのは酷な話です。その様な場合は、圏 M から 圏 W への射が単射であれば十分でしょう。その様な場合は、”Art of Conceptual Modeling”のモデリング体系ほど厳密なモデリング体系である必要はありません。少なくとも、圏として定義可能なモデリング体系を採用すれば十分でしょう。
”みんなの圏論”では、olog というモデル記法が紹介されています。olog の詳細は、
[1102.1889] Ologs: a categorical framework for knowledge representation (arxiv.org)
の論文で紹介されています。このモデル記法は、圏論に則って構築されていていて、本セクションで考察した、圏 M のモデルを描くのに最適な記法の一つと思われます。(olog に宗教的に心酔する人がいたらごめんなさい。悪気はありません)
ここまで書いてきた、対象世界のモデル化の内容を考えるにあたっては、”みんなの圏論” の7.1.1 節の「バブバブ」と「大人の音声」に関する考察が非常に参考になりました。
このアナロジー(?)に則れば、圏 W は集合圏で、L を自由関手とすると、
L:W→M
がモデリングという行為に相当すると考えられるのではないかと現時点では考えています。
皆さん、結構面白いので読んでみてくださいね
紹介した論文によれば、olog は、”A categorical framework for knowledge”の道具なので、対象世界の知識を圏論的に表現する道具であるといえます。olog によって、対象世界を圏論をベースにモデル化できるということを前提にすれば、olog と自然同値、あるいは、圏同値なモデリング記述体系を使えば、同等な事が実現可能であると考えられるでしょう。
概念モデリングと olog の関係
”Art of Conceptual Modeling”の概念モデリングで作成するモデルは、
概念情報モデル
データ型定義
複数の特徴値の組を持つ概念クラス
概念クラス間の Relationship
ドメインオペレーション
概念振舞モデル
振舞を持つ概念クラスに対する状態モデル
状態毎のアクション
ドメインモデル
ドメイン(概念情報モデル)群と実装時のドメイン間の関係
から構成されています。説明を簡単にするために、概念モデルの圏を 圏 C と呼ぶことにします。
概念モデリングの観点からすると、圏 W と 圏 C は、圏同値の関係にはありません。何故なら、圏 W は、圏 C で記述された対象を雛形にした、概念モデリングの用語でいえば、概念インスタンス、及び、その概念インスタンスの値を持った特徴値、概念インスタンス、のリンクの集合(それぞれが 圏 C で明確に要素か否かが判断可能なので集合)が同値だからです。この、”概念インスタンス、及び、その概念インスタンスの値を持った特徴値、概念インスタンス、のリンクの集合”を 圏 I と書くことにします。

すると、圏 W と 圏 I は圏同値、圏 I と 圏 C の関係は、関手の例で取り上げた、具体的な有向グラフの圏 と DiGraph の圏の関係と同じになっています。
上の説明では、概念情報モデルの要素だけを取り上げましたが、状態モデル、状態アクション、ドメインオペレーション等も、全て雛形であり、時間の経過に伴う圏 W のダイナミクスを通じて顕現する全てのオブジェクトは、圏 C 上で定義されたオブジェクトを雛形とするインスタンスに対応することになります。
一方、olog は、

こんな図を描きます。四角は、Type であり、オブジェクトの集まり(圏を意識し集合とは書かない事にします)を意味し、矢印は圏の用語の”射”を表します。この二つの道具を使って、Knowledge に関する aspects と facts を表現します。
本来なら数学的に厳密な議論や定義をするべきでしょうが、悲しいかな私は数学者ではなく、そんなスキルは無いので、印象と勘での意見で申し訳ないのですが、ざっくり言うと、olog は、”圏 C のモデル記述要素を延べ単にしたもの”と位置付けて問題ないと考えています。
つまり、olog の圏(圏 O と呼ぶことにします)と 圏 C は自然同値だろうと、いう事です。
ここではそうだという前提で話を進めますね。
「じゃあ olog だけでいいんじゃない?」って話になりそうですが、実用を考えると、そうもいかないでしょうね。
概念情報モデルでも、結果的にはできてしまうのですが、olog を使うと、概念インスタンスと概念インスタンス間のリンクのレベルの図も自然に描けてしまうという印象を受けます。概念モデリングがうまくできるかどうかは、この、概念インスタンスの世界と概念クラスの世界を区別できるかどうかにかかっているので、その区別がはっきりしたモデル記述体系を使ったほうが迷わなくて済むのは間違いありません。私の圏に対する理解が進まないのも、書籍の説明がその点に関して曖昧なものが多いというのが理由の内の大きな要因だったりもします。
他にも、実用上で言えば、圏 C のモデル記法に従って描いたモデル図を olog で書こうとすると、延べ単であるがゆえに、巨大なモデル図になってしまうだろうという事は容易に想像がつきます。実際”みんなの圏論”でも似たようなコメントが書いてあるので確かです。極端な例を挙げると、通常のプログラムコードと同様な内容(圏同値)の olog のダイアグラムを書くことは可能ですが、読みにくいだけなのは明白でしょう。他にも、圏 W 上の事象による状態の変化は状態遷移図で書いた方が、また、データが複数の演算(operator)で変換(’計算’という言葉を使うより圏論ぽいので’変換’)されていく様はデータフローで描いた方が直観的で判りやすい図が描けます。
道具は適材適所で使いこなす事で作業効率が上がります。
モデル化したい世界の一部だけを精密に見てみたい、とか、ディスカッションでのスケッチ等では、olog は有効と思われるので、私も推奨したい(olog を書く前に、モデル化対象の世界で馴染みのあるイラストやアイコンを使って絵を書いてから olog を書くと、より効果抜群)と思っていますが、モデル化対象全体を、きちんと記述するには、やはり、”Art of Conceptual Modeling” のモデリング体系の記法を使うのがお勧め、というのが現時点での私の結論になっています。olog の表現図が欲しいなら、”Technique of Transformation” のプラクティスを使って、圏 I のモデルを、圏 C を元に olog の図に変換(多分逆は無理)してやればよいだけの事です。
対象が小規模な場合には有効なツールが、対象が大きくなってくると有効ではなくなるという事は実務ではよくある事です。
モデルの記述方法においても、ある程度までの規模では、図による表現が直観的で判りやすくて良いのですが、規模が大きくなってくると人間の認識能力を超えてしまうので、巨大な図を適切なサイズに分割したり、表や階層構造を持ったテキストで記述したりと、何らかの工夫が必要になります。
テキストにおいてさえさらに大規模化すれば、人間の限界を超えてしまうので、前のセクションで紹介した、個々の有向グラフに対する DiGraph 圏の様な、構造や表現に着目した圏(こちらの方が圧倒的に規模が小さい)をターゲットにするなどの工夫が更に必要になります。
物理学においては、日常の規模はニュートン力学、宇宙規模は相対性理論、極小の世界は量子論と、スケールに応じた使い分けが行われています。また、表現においても、図や数式を適切に使い分けています。
ニュートン力学の”剛体”や量子論の”電子”は、圏 W や 圏 M (実際に世界に存在している個々の物体や電子)ではなく、圏 C (分類し抽象化している)であるといったら、ピンとくるでしょうか。
閑話休題
手法や技法は、一見華やかで使いたくなってしまうものが多いですが、それを実務に導入する場合は、常に、記述対象が大規模になった時に、果たして有効に作用するのかを常に考慮しなければなりません。
「データが巨大化したらビッグデータだからクラウドコンピューティング使えば解決」?いやぁ…そんなことは無いでしょう。
その辺りについては、”Practices of Software Engineering”で説明しているので是非読んでみてくださいね。
概念モデリングの基礎を圏論で整える
これまでのセクションで、”Art of Conceptual Modeling”の概念モデリング体系、及び、モデリングで作成する様々な図や定義は、圏や関手であろうと考えられることを説明してきました。このセクションでは、圏論によって、概念モデルの記法を、厳密に定義できるであろうことについて考察していきます。
何故、そんなことをするかと言えば、自然言語で書いた説明文はどうしても曖昧な部分ができて、読んだ側に色々な解釈ができる余地を与えてしまい、誤解を与える可能性があるからです。説明文を諄く詳細に書けば、曖昧さはある程度排除はできるのですが、そんな文章は多くの読者には嫌われて読まれない恐れがあります。その点、数学的な記述であれば、簡潔な式で厳密な定義を行えます。
一方で、数学的な記述は、判る人にしか判らないという問題が新たに生じるので(苦笑)、
モデリング体系に対する、数学の観点からの厳密な定義
自然言語の説明文によるモデリング体系の解説
という二本立てが理想であろうと、いうことです。通常は二番目の解説を使い、「あれ?ここどうなっているの?」と迷った時には一番目の定義を参照して疑問や曖昧さを排除します。この様にしておけば、20世紀末から20世紀初頭に起こった、宗教がかったバカげた方法論戦争の勃発も防げるのではないかと思っています。
実用的な観点からすると、上の二番目は3系統ぐらいの説明の流儀を変えた解説と、上の二つに加えて、沢山のサンプルがあると超強力。
さて、ここからは、概念モデリングで使う各モデルについて、圏論による基礎の定義の可能性についてみていきます。
念のため書いておきますが、概念モデル(圏 C)はたった一つの圏で定義されるようなものではない事が明らかです。複数の圏を使って重層的に定義されるようなものです。概念モデル上の同じ要素が複数の圏の対象(object)として表れます。
概念情報モデル
前述の通り、概念情報モデルは、
データ型定義
複数の特徴値の組を持つ概念クラス
概念クラス間の Relationship
ドメインオペレーション
から構成されています。
先ずは、最初のデータ型定義です。
データ型は、
識別子や列挙子、数等に対応する離散値向けの型
温度や位置、加速度等の連続値向けの型
文字列型
それぞれのデータ型を持つ複数の変数からなる複合型
等に分類する事が出来ます。1番目と3番目については、”圏論の道案内” P77、P82の「④関手の例3:モノイド準同型(1)」、「⑤関手の例4:モノイド準同型(2)」と、P136「⑥自然変換の例4:単位系の変換」あたり(加えて、線型代数対話のシリーズ)に詳しい定義が載っているので、それを再利用できます。4番目は、多分、数系、量系の直積。
3番目の文字列は、…、あれ?探しても見当たりません。文字列に対する圏的考察が無いわけないので、とりあえずは放っておくことにします。
…と思いきや、データの型としての説明ではないですが、モナドの説明の中で、”圏論の歩き方”の P76 ‐ 第5章 モナドで、文字列が扱われています。
次は、「複数の特徴値の組を持つ概念クラス」と「概念クラス間の Relationship」です。これは、一般的な リレーショナルデータベース のスキーマの定義とほぼ同じなので、
みんなの圏論
4.5 データベース:スキーマとインスタンス
5.4 圏とスキーマの同値性
活躍する圏論
3 データベース:圏、関手、普遍的構成
で解説されている Sch(スキーマ圏)のほとんどが再利用可能です。
異なるのは、スーパークラス、サブクラス の Relationship です。これについては、”線型代数対話 第3巻 量系のテンソル積”の”3.分割”の定義5 が、どんぴしゃりな定義になっています。
あとは、関係クラス。

図のように考えれば、3つの概念クラスの二つの二項関係に分割として記述はできるものの、一つだった Relationship の R1 が、R1' と R1'' の二つの Relationship に分割されてしまい、同値ではなくなってしまうので、別の圏論的な記述が必要になるのではと思っています。
書籍で紹介されているデータベースの例があまりにもシンプルなので、そこで解説されている圏で十分なのかは今のところ不明です。
更に、単純な二つの概念クラス間の、片方の多重度が’1’で、他方の多重度が ’*’(0 または 1 以上)の場合を考えると、

となり、概念クラス A の概念インスタンスからは、複数の概念クラス B の概念インスタンスは複数となって、概念クラス A の各概念インスタンスに対し、射が無いか、射が複数ある事になります。逆方向では、概念クラス B の概念インスタンスは、概念クラス A の概念インスタンスに対するただ一つだけの射がある事になります。圏論的には、これでもいいのかなぁとは思うのですが、対称性が悪いなと、思うのは私の勝手でしょうか?
各書籍の Sch圏 に関する説明は、テーブル(概念モデリングの概念クラスに相当)を主体に論理が展開されている様に見えます。
むしろ、リンク(データベースでは外部キーによる参照)を主体にして、考えた方がすっきるするのでは?

ある意味、ネットワークモデル(有向グラフの向きがない)的な扱いで、考えるという事です。要するに、一つのリンクに対して、二つの端がある(二つそれぞれに多重度がつく)という事です。
最近私は、概念情報モデル(人間の Knowledge の表現という意味で)の肝は、概念クラスではなく、Relationship なのではないかと考えていて、それにも合致するのかなという感触です。
この方向で、今後も学習・調査・検討を続けていく予定です。
概念情報モデルは、面白い性質を持っています。”ドメインと IT システム構築”や、”Technique of Transformation” で説明している通り、概念情報モデルの構成要素の、データ型や概念クラス、特徴値、Relationship 等を概念インスタンス(圏 I)とした概念情報モデルを記述する事が出来ます。
そもそもが、「概念情報モデルはあらゆる対象世界(人間が認識できるという意味において)をモデルとして記述できる」と標榜しているので、記述できなければ自己矛盾なのですが。この様なモデルを我々の流儀では古来(笑)から”メタモデル”と呼んでいます。一見、自己言及する再帰的な定義に見える(私も昔の一時そう思っていた)のですが、定義自身は、この第一段目の”メタモデル”のレベルで止まるので、再帰にはなってはいません。
”メタモデル”の、圏論的な基礎付け、多分、関手圏とか、その辺りで考えるとすっきりするであろう、定義があると、他者への説明も楽になりそうです。
その流れでいえば、前述の olog も概念情報モデルのメタモデルに相当するダイアグラムをかけるはずです。残念ながら前述の olog の論文には、それに相当する説明が見つけられないので、なんだか残念です。
次は、ドメインオペレーションですが、これは、状態アクションと基本が同じなので、後の説明に譲ることにします。
状態モデル
概念振舞モデルの一つ、状態モデルです。概念モデリングの状態モデルは、基本的には、有限状態機械と同じです。従って、”圏論の歩き方” 第6章「モナドのクライスリ圏」をとっかかりにすればよいと思われます。
内容的にはちょっと微妙(このコラムにとってという意味で)なのですが。
有限オートマトン - Wikipedia によれば、有限状態機械のバリエーションは結構多くて、それぞれの特徴を有しているため、概念振舞モデルの状態モデルに関する圏論による定式化は、状態遷移の際の、”Ignore”、”Can’t Happen” や、遷移を引き起こす事象(イベント)、状態モデルの実行セマンティクス等を考慮した検討が必要そうです。
まだまだ私の圏論に対する理解が不足しているので、今回はここで止めておきます。
アクション(状態アクション、ドメインオペレーション)
概念振舞モデルの状態モデルでは、ある事象が発生した時に、状態モデル(圏C の存在)を雛形にして、対応する概念インスタンスの状態を保持する状態機械(圏I の存在)が一個存在すると考えます。状態機械が事象によって遷移を起こした時、状態遷移先の状態に紐づけられたアクションが実行され、そのアクションが実行完了した時点で、状態遷移が確定するものとして定義されています。
また、ドメインオペレーションは、複数の引数と共に起動される、圏C の定義に基づいて、圏I の要素への参照・更新を行う一連のアクションとして定義されます。
この、”アクション”を記述する場合、実用的には、ビジネスをモデル化する ~ BridgePoint を使ってみよう|Knowledge & Experience (note.com) で紹介している様に、アクション記述言語(OAL: Object Action Language)の様なテキスト形式の言語で記述するのですが、セマンティクスは、データフローモデル(Data Flow Model)が基本です。いくら OAL が一般的なプログラミング言語に見えようとも、(そして実際そんな風に思っても書けてしまうのが微妙ですが:苦笑)上から順に処理が実行されていく普通の一般的なプログラミング言語とは異なります。実行順序は、データフローモデルのデータの流れによって決まるような実行セマンティクスが定義されています。
私の手元にある書籍群では、データフローモデルに関する圏論の議論が書かれたものが残念ながらありませんでした。単なる図の構造の話であれば、それぞれの矢印にデータが紐づいた DiGraph として扱えるとは思うのですが。後は、強いて言えば、”活躍する圏論”の第4章協調設計や、第5章信号流れ図あたりが参考になるか、という感触があります。
こちらも、私の圏論に対する理解が不足しているので、今回はここで止めておきます。
ドメインモデル
最後は、ドメインモデルです。概念モデリング以外の流儀では、何故か、”ドメイン”という言葉が意味するものを、”アプリケーション”に限定するものが多いです。システム開発の文脈でのドメインは、一般的には”問題領域”と訳すことが多いのですが、システム開発ではアプリケーション領域以外でも解決しなければならない問題はごまんとあります。アプリケーション領域も含め、システムを実現するのに必要な、再利用可能な一般化された概念群、ミドルウェア、プログラミング言語、コンピューティングプラットフォームは全て、個々の”ドメイン”と考えても何ら齟齬は生じないでしょう。そしてそれらを、このコラムで解説してきた、圏 I の構造を記述する 圏 C 的な考え方を適用して、圏 C に相当する圏(構造を表現する圏)をそれぞれについて定義すれば、それぞれのドメイン(圏 C で記述) は独立した存在と見なすことができます。
一方で、システムとして出来上がったソフトウェア(プログラムコードや設定の集まり)は、プログラミング言語やコンピュータプラットフォーム(圏C で記述:便宜上、この圏を 圏 P と呼ぶことにします)を雛形とする 圏 I です。判り難いので、この圏を、圏 E (それぞれの具体的なプログラムコードや設定の集まり)とします。
この様な観点からすると、システム開発によるシステムの構築は、本来無関係なドメインモデル(圏C)群を組み合わせて、圏 E に変換する事、と言ってよいでしょう。
この説明において、組み合わせるのが 圏 I でない理由を考えてみてください。プログラムコードは、圏 P に対する 圏 E だと説明しましたが、高品質なコードは、圏 E の中に、圏 C 的な部分と、圏 I 的な部分が適切に分割されて含まれているはずです。
参考資料:”Essense of Software Design”
実は、これが、”Technique of Transformation” で解説している”変換による実装”の数学的な解釈であろう、というのが現時点での私の結論です。
ドメインとITシステム構築|Knowledge & Experience (note.com) の図9 は、正にそんな様を図にしたものだといえるのではないでしょうか。
この説明で理解できる読者がどれだけいるんでしょうね…
リレーショナルデータベースシステムを思い浮かべてください。実際に使えるリレーショナルデータベースのソフトウェアは、Microsoft SQL Server、Oracle Database、My SQL、PostgreSQL 等様々です。また、クラウドが実用化された現代においては、クラウド版の対応するサービスが利用可能です。それぞれがどんな風に実装されているか覗くことが出来れば、それぞれ全く違うコードで構成されている事でしょう。
リレーショナルデータベースは、そもそもが、1970年に Edgar Frank Codd が提唱したRelational Theory がベースになっていて、それがリレーショナルデータベースの理念の圏(圏C)であり、それぞれの具体的な製品・サービスは、サーバー上で動く場合はサーバー用のコンピューティングプラットフォーム、クラウドで動く場合は、クラウド用のコンピューティングプラットフォームの圏にマップした 圏E であることになるでしょう。
また、アプリケーション領域というのは、ビジネスシステムにしろ、制御システムにしろ、皆さんの現実世界における解決するべき課題・問題の解決策を意味します。コンピュータやネットワーク技術が解決してくれるのは、その解決策を実行する際の、時間と空間の制約の部分だけです。そもそもが、アプリケーション領域(ドメイン)と 圏 P は無関係でそれぞれ独立した存在であるという事です。システム開発に携わるからと言って、いくらプログラミング言語の文法に精通しても、また、コンピューティングプラットフォームに精通しても、開発対象のビジネスや制御の理解が深まらないのもそのせいです。
複雑な業務プロセスをそのまま放置して、デジタル技術を適用してシステムを開発しても、複雑で使い勝手の悪いシステムが出来てしまう原因はこれなんですね。
実は、”ドメイン”とは何かについて、私はまだ、厳密な定義を語る事が出来ません。
概念モデリングで記述された、概念モデル一式で定義される対象領域
データの観点(圏論でいうところの”対象(object)”と”射”一式)→ 概念情報モデル
振舞も含めたドメインの記述 → 概念情報モデル+概念振舞モデル
現段階では、これが、「ドメインとは何ですか?」と聞かれた時の私の精一杯の回答です。
圏論に関する様々な書籍・コンテンツを読んでいて、”ユニバース”という言葉が出てきたので、「これがドメインか」とも思ったのですが、今のところ、
ドメイン = 何らかの特徴を持った圏:便宜的に 圏 D と呼ぶことにする
なんだろうなと。概念モデリングでは、ドメインの外から
ドメインオペレーションを起動する
概念インスタンスへの事象を送信する
事が出来、また、アクションの中からは、External Entity を通じて、ドメイン外の操作を起動出来たりするので、この圏 D は、複素数の代数演算の様な完備性はありません。なので、これも「ドメインとはxxxだ」という定義には使えません。
ちょっと考え方を変えて、実用上の観点から考えてみます。
モデリングにおいて実用上で問題になるのは、モデル化対象世界のオブジェクト(圏の用語の対象(object))が、目下作成中のドメインにおいて、特徴値、あるいは、概念インスタンス、はたまた、リンクなのかが判断できるか(事象等、アクション系の話は同様な理屈を適用すればよいので割愛)という事です。
ここに圏論の考え方を適用してみると、
着目している対象世界側のオブジェクトが、作成中の概念情報モデルで既に抽出されているモデル側のオブジェクト(特徴値、概念インスタンス、リンク等)の間で、”射”があるか
が判断基準として使えるのではないかと考えています。射があれば、同じドメイン、射が無ければ異なるドメインという事です。
「射があるかどうかをどう判断するか」は、どんな観点・コンテキストで対象世界をみているかによることになります。
結局は個人個人の認識の話なので、”3. モデリングとは ~ 現象学からの考察|Knowledge & Experience (note.com)”で書いている様に、とりあえず記述して、みんなの合意を得る、ですかね。。。
ドメイン分割を圏論的な観点で考察してみる
個人個人の認識というと、「それってあなたの感想ですよね」とか言われて終わりそうなので、もう少し考察を進めてみます。
例として、ビルマネジメントにおける部屋の温度を考えてみます。
適切なコストで利用者が快適に過ごせる部屋を提供しようというビジネスの一部とします。
このとき、概念クラスの候補として、ビル、部屋は簡単に思い浮かべられると思います。また、ビルと部屋には1対多の R1 という Relationship が存在するというのも異論はないと思います。更に、各部屋(部屋という概念クラスを雛形にした概念インスタンス)の特徴値として温度(単位を摂氏とする実数)の値を持ち、よって、部屋という概念クラスは温度という特徴値を持つ、という事もまた異論はないと思います。他にも、ビル、部屋ともに個々の概念インスタンスを識別する為の名前を意味する特徴値も、持っています。
ここまでで出てきた、ビル{名前}、部屋{名前、温度、ビル名}、Relationship(※ 部屋のビル名でフォーマライズ)は、この注の冒頭に上げた対象世界が成すシナリオやコンテキストにおいて、射を定義する事が出来るので、同じドメインに所属していることになります。このドメインを BM と呼ぶことにします。
この文章、技術屋さんではない読者の皆さんには特に気になる点はないと思います。しかし、技術系の読者の中には、「え?温度っていうけど、どうやって測るの?」という点が気になって仕方がない人が結構いるのではないでしょうか?
実際のシステムでは、部屋ごとに何らかの装置が設置され、その装置には温度センサーが組み込まれていて、装置内のプログラムが、温度センサーがデジタルセンサーなら、I2CやSPI等の HWインターフェイスを介してデジタルデータを、アナログセンサーなら、ADC で変換したデジタル値を読み取り補正をかけて温度を算出し、ネットワークを通じてサービスを統合しているシステムに送る、といった仕掛けが存在するかもしれません。
では、この温度を測る仕組みを成り立たせているオブジェクト(センサーや装置)は、ドメイン BM に属するでしょうか?
答えは、No でもあり Yes でもあります。冒頭のステートメントがシンプル過ぎて判断できない、というのが、実務レベルのモデリング活動での正解です。
冒頭のステートメントは、「適切なコストで」始まっています。温度を測る装置はきっと幾ばくかの電力を消費するはずなのと、ある程度の広さの部屋(という事は、部屋の特徴値として”広さ”:データ型は面積を持つことになる)では、温度は一様ではないと思われるので、複数の装置が設置されてそれぞれの設置場所の温度を計測する事になりそうです。この流れで、ドメイン BM の概念クラスの候補として、装置{設置位置、部屋名、消費電力、温度}が考えられ、部屋とは1対多の R2 という Relationship で関係が張られることになります。装置.消費電力は、現在の装置の消費電力を W を単位として保持し、部屋の温度は、R2 でリンクされた装置インスタンスの温度の値の平均値(単なる平均ではなく装置の設置位置を考慮した平均値計算でも可)にすることにしましょう。

このモデルにおいては、装置を追加する前に問題になっていた、部屋.温度 の計測問題は、装置.温度 に移動していますが、相変わらず、温度の測り方に関する疑問は残ったままです。
この疑問に対して明確な回答を与える前に、上の図で定義されている概念クラス、特徴値、Relationship についてみてみることにします。圏論的な観点で眺めると、これらすべては、冒頭のステートメントのコンテキストで考えると、それぞれのオブジェクトが全て、そのコンテキストの上で意味が成り立つ一つの射で変換(対応)が可能なものになっています。
一方、装置.温度 に対する、装置内部のセンサーの種類やセンサーからの温度計測ロジックは、センサーデバイスの供給メーカーや型番が違えば全く異なるものが複数代替可能な形で存在します。ざっくり、壁掛けの温度計を定期的に人が見て測る方法でも ドメイン BM にとっては、ドメイン BM のシナリオやコンテキストが成り立つなら計測方法はデジタル方式でもアナクロ方式でも何でもよいでしょう。これを圏論的に書き直すと、
装置.温度 という特徴値に対して、”計測する”というオブジェクトが存在し、装置.温度 が定まれば、必ず、”計測する”に変換(対応)できる射が存在する
システムを実装する際に、一つの”計測する”に対し、複数の”計測方法”が候補として存在する。つまり、”計測する”と”計測方法”の候補という写像は、1対多である。
システム実装時には、その候補の中から一つが選択されて、システム実装に使われる。つまり、”計測する”から”計測方法”への”実装する”という射がただ一つだけ定まる
になる(間違ってないよね?)でしょう。
ドメイン BM にとっては、”部屋(装置の周り)の温度が何℃か”が、関心事の中心であり、ドメイン BM のシナリオやコンテキストを乱さない精度やコストを満たすなら、計測方法はなんだってよい、逆に言えば、”精度やコストを満たすものを適切に選択してシステムを実現する”、という事です。
この様に考えた場合、ドメインオペレーションや状態アクションを記述する際には、装置.温度 というある概念インスタンスの特徴値の値は、参照した時には、現実世界の部屋(装置周辺)のその時点の温度が保持されているものとして、アクションを記述・定義してかまいません。
以上を踏まえると、あるオブジェクトが、着目しているドメインに属するか属さないかの判断基準は、
ドメインのシナリオやコンテキスト上の意味において、圏 W に存在するオブジェクトただ一つだけの射(関手?)が存在する → 同じドメインに属する
既にドメインの一員と判断されているオブジェクトとの間には、システム構築の際に”実装手段”として選択されるような意味(ここでは”実装する”)における射(関手?)が複数存在する → 異なるドメインに属する
で良いでしょう。
概念情報モデルで定義された 1対多の Relationship の場合、ドメイン BM で言えば、ビルと部屋の間をつなぐ R1 がそれに相当しますが、圏 W のビルに対応付けられる(つまり射がある)概念クラス ビル の一つの概念インスタンスは、概念クラス 部屋 の複数の概念インスタンスに対応付けられる、つまり、一つのビルに対して複数の部屋への射が存在するので、上の説明は間違っているんじゃないかと思う読者がいる(3か月後の私も含めw)かと思います。
この複数の射は、圏 C を理念とする 圏 I 上の概念インスタンス間の射であって、判断条件の一番目で言及している射とは異なります。
判断条件の一番目を、ドメイン BM の ビル、部屋、R1 について書き下すと、
- 現実世界(圏 W)の”ビル” ↔ 圏 I のビル(圏 C のビルの概念インスタンス)
- 現実世界(圏 W)の”部屋” ↔ 圏 I の部屋(圏 C の部屋の概念インスタンス)
- 現実世界(圏 W)の”ビル内の部屋” ↔ 圏 I のリンク(圏 C の R1 の概念インスタンス)
となり、圏 W と 圏 I のそれぞれのオブジェクトについて、1つづつ射(関手?)が存在している事になり、ビル、部屋、R1 は、ドメイン BM を構成するオブジェクトであることが確認できるわけです。
逆に、温度を測る装置の内部的な仕組みについて考えてみます。この装置の仕組みの方を考えています。さて、”装置の仕組み”を考える時、ドメイン BM のオブジェクト群は絶対に必要でしょうか?
”装置の仕組み”の本質的な役割は、温度センサーの場合、”温度センサー付近の温度を測ってデジタルデータ化する事”だけです。別に温度センサー付近が部屋でなくても、外気の温度でも、地面の温度でも、何らかの装置のチャンバー内の温度でも別に構わない(センサーには動作可能温度範囲があるので、乱暴かなw)なんでもいいわけです。必要なのは、”装置の仕組み”を考える上での要件となる、計測可能な温度の範囲と精度、設置環境の条件(防水とか、大きさとか、見た目とか)等の情報のみです。
これを圏論的に見ると、
”装置の仕組み”に関するシナリオやコンテキストにおける意味においては、”装置の仕組み”のオブジェクトからドメイン BM のオブジェクト への 射 は存在しない
という事になります。”装置の仕組み”を構成するオブジェクト間には、そのシナリオやコンテキストにおける意味においてのただ一つの射が存在するでしょうから、”装置の仕組み” は、ドメイン BM とは独立したドメイン(仮に EQ と名付けることにします)を構成することになります。
この様なドメイン間の独立性の事を、昔からの私のモデリング仲間の間では、”直交する”なんて言い方をしていました。
このコラムでは、それを圏論の言葉で書き換えてみたわけです。
あ、読者が誤解しているといけないので、念のため注意しておきますね。このセクションの文中に出てくる”オブジェクト”という言葉の意味は、圏論の”対象(object)”の事を指しています。オブジェクト指向プログラミングのオブジェクトではないという事にご留意くださいませ。
この辺りの話は、圏論を知らなかった頃に書いている、”ドメインと IT システム構築” の内容とも齟齬は無い(当たり前かw)ので、実用上は問題がないでしょう。
このセクションの例では、温度センサーを例に挙げましたが、
製品製造ラインを構成するロボットと、ロボットアームを動かすモータ制御
設備管理や装置の調達・設置
稼働状況の記録
…
等々、様々な場面で、ドメインに属するのか属さないかの判断が迫られますが、”実装する” ための候補としての複数の射と、”実装する”為の選択という一つの射という考え方で全て判断基準は、私の経験上、全て適用可能です。
”実装する” という言葉は、ソフトウェアよりな言葉なので、もう少し意味的な広みを加え、”実現する”という言葉を使う事にします。
概念モデルを”実現する”(実際にITシステム上で動くようにする)には、そもそもが、圏 I のデータをどうやって保持するのかについても、”実現する”という射で、複数のドメイン(圏 P)との関係を考えることができます。一つのコンピューティングノードで実行する様なシンプルな実装であれば、データは実行中のメモリ上で保持するだけでいいので、圏 C の構造から導出したプログラム上の class の instance を new するだけでいいですが、”IoT・Digital Twins 最初の一歩”で解説している様な、ビッグデータ系の IoT・Digital Twins ソリューションであれば、
リレーショナルデータベースを使う
Cosmos DB の様な NoSQL 系のデータベースを使う
等、様々な選択肢が存在します。リレーショナルデータベース を使うなら、レコードを作成する SQL 文を組み立てたり、ロジック実行時のメモリ上の変数との同期等のロジックが必要です。
…と、あたかも圏論全部理解してるよ的な感じで書いてきましたが、もしかすると、間違っているかもしれません。
ここで書いている様な話は、多分(いや確実に)世界でも誰も考えたことがない(取り上げている主題自体がニッチなので)はずなので、今後の議論のとっかかりになればいいなと、思ってます。
その他のトピック
以上、圏論から見たモデル化について、概念モデリングの基礎固め、と書いてきました。このセクションでは、圏論の書籍群を読んで思ったこと等を書いてみます。
”変換による実装” と ”Round Trip”
ドメインモデルのセクションで、概念モデリングと変換による実装によるシステム構築について書きました。この開発プロセスを圏の関係で改めて書くと
圏 W → 圏 I でオブジェクトを見つけ、圏 I の理念の圏である 圏 C を定義
システム構築に必要な 圏 W 全てに対し 圏 C を定義
圏 C を 圏 P 上の 圏 E に変換
になります。複数の事項を単数で書いているので判り難くて申し訳ないですが、我慢してください。
説明を短くするため、3. の”変換”、これは、関手圏であろうということで、”圏 T ”と呼ぶことにします。
この三番目のステップは、変換による実装 で解説しているテクニックで自動化が可能なわけです。結果として、モデル化対象世界(概念モデリングのアプリケーションドメイン:つまり、ビジネスや制御という現実の世界)に対して概念モデル(概念情報モデル+概念振舞モデル)を作成すれば、実装で使用する実装プラットフォーム上に変換するルールをコンピュータ上で実行可能な形式で作成すれば、コーディングを自動化できることになります。
この変換は、私の現段階の圏論の拙い知識レベルから判断するに、自然同型な変換、だと思っています。自然同型であるとは、この変換は、圏 C から 圏 P への一方通行の変換であることを意味します。このことは、生成したコード一式を、概念モデルに変換する方法はないことを意味します。
例えば、”足して100になる二つの数の自然数の値は幾つか?”、足し算でなく掛け算でもいいのですが、足し算の場合は、自然数の組の候補は、(1,99),(2,98),…,(98,2),(99,1) の99通り、掛け算の場合は、(1,100),(2,50),(4,25),(5,20),(10,10),(20,5),(25,4),(50,2),(100,1) の9通りあって、元の自然数の組を一意に決められないのと理屈は同じです。
さて、このセクションのタイトルに書いた、”Round Trip”に関する考察です。Round Trip とは、モデル駆動型開発において、
システムの構造、振舞をモデル図で描く
モデル図をコードに変換する
コードを実行し間違いを見つけたら修正する
コードの修正をモデル図に戻す
というサイクルを繰り返して開発を行うスタイルを意味します。古くは、OMT 法をベースにした、Rational Rose というモデリングツールで採用されていました。その後 Rational Unified Process(昔々 Rational って会社があってのぅ…ずいぶん昔に IBM に吸収されたんじゃぁ…)という開発プロセスに受け継がれている(多分)はずです。
…このプロセス、このコラムのこれまでの説明からすると、不思議に思いませんか?
前のセクションで、私は
… 変換は、私の現段階の圏論の拙い知識レベルから判断するに、自然同型な変換、だと思っています。自然同型であるとは、この変換は、圏 C から 圏 P への一方通行の変換であることを意味します。このことは、生成したコード一式を、概念モデルに変換する方法はないことを意味します。
と説明しましたよね。という事は、モデルから変換されたコードに修正を加えた場合、その修正項目を正しくモデルに反映させる術はない、という事を意味するわけです。”変換による実装” を流儀とする私としては、20年来ずっと、”んなわけあるか”、略して”なわけ”と思っていた、というか、何故、こんな理屈が通らない開発プロセスが世の中で堂々と発信されているか、不思議でなりませんでした。
…まぁね、当時こういうことを言うと RUP 推進派の人達と大喧嘩になってしまうから、柔らかく否定ぐらいしかしてませんでしたけど…
ちなみに、”変換による実装”の場合は、生成されたコードに間違いがあった場合(どんな能書き的に優れたやり方でやってもテストは必要って事で)は、
組み合わせているドメインの内、間違えているドメインがあればその 圏 C のモデルを修正
実装方法で間違いがあれば 圏 T を修正
修正した、圏 C のモデル群を、圏 T の変換ルールでコードを再生成
という手順を踏みます。繰り返しになりますが、モデルからコードへは一方通行なので、”Round Trip”とは言えません。
最近漸く謎が解けたので、ここに書いておこうと思います。要するに、”変換前のモデルが何を対象としたモデルなのか?”に尽きるという事ですね。
”概念モデリング”の対象が、開発対象となるビジネスや制御の現実世界であるのに対し、”Round Trip”系のモデルは、圏 E のモデル(プログラムコードと同等のオブジェクトを図表現している)だという事です。その場合のモデルは、単に図で表記されたモデルとテキストで表記された、圏同値のモデル間の変換になるので、相互に行き来できても不思議でもなんでもないのは当たり前です。
この話、そうだよなぁ…とはずっと判っていたことなのですが、今回、圏論的に考えることによって、すっきり定義できたというお話でした。
まぁ、私の圏論に対する理解が正しければの話ではありますがw
…と書いておいてなんですが、実は、”変換による実装”でも、やろうと思えば”Round Trip”はできるんですよ。どうするかというと、
圏 E が 圏 C と 圏 Tの積(product)になるように、圏 T を定義する
という方法です。

図中の P が 圏 E に、A、B が 圏 C、圏 Tに当たると読んでください。こんな 圏 T であれば、生成されたコード(圏 E)を射影を使って元に分解できることになりますから。
…そうですね…実務的な効率で言うと、圏 C 由来の間違いを正すのはそれほど工数のかかるものではないので、恩恵薄ですが、圏 T 由来の間違いを正すのは結構大変なので、この考え方を応用した何らかの方法(現時点では思い浮かばない:苦笑)を組み込むと、変換ルールの作成で便利かなと。
実は、”変換による実装”ではない普通の”Round Trip”的なやり方には、もう一つ問題があるんですね。
”Round Trip”で作成するモデルの 圏 E というのは、既に使う事が決まっている、ミドルウェアやコンピューティングプラットフォーム、プログラミング言語に固定されたモデルだという点です。IT 技術は日進月歩でどんどん新しいものが出てきます。新しいテクノロジーに乗り換えなければならない日は必ずやってきます。これは、圏 P を変えるという事になるので、それに依存している(一体化している?) 圏 E を変更するのは、とても大変な作業になる訳です。下手をすれば(大抵そうなんですが)、圏 E のモデルを一から作り直した方が早いんじゃないかという状況になりがちです。規模が大きければ大きいほど大変。苦労に苦労を重ねて作ってやっと動かした 圏 E の場合は、「またやるのそれ?」ですよね。
昨今では、旧来のシステムを丸ごとコンテナ化して動かし続けるという話も聞きますが、保証が切れたOSやミドルウェアが動き続けるという意味では本質的な解決にはなっていないように思えます。
Open AI(別の系統の AI でもいいですが)を、圏 E のモデルから、積の射影を使って、圏 C 的なモデルと、圏 T 的なモデルを自動生成する様な事が出来たら便利なのですが。。。
更に付け加えておくと、”変換による実装”においても、圏 E に相当するモデルは活用します。圏 C のモデルを 圏 T によりコードを生成する場合、毎回全てのソースコードを生成することはありません。Bridge Point で作成した概念モデルを In Memory で動作する C# アプリケーションライブラリに変換する|Knowledge & Experience (note.com) の様に、予め作っておいたアプリケーションフレームワークライブラリを拡張する部分のコードだけを生成するのが常套手段です。この様なアプリケーションフレームワークライブラリの設計では、フレームワークを構成する class 群の構造と基本的な制御スレッドといった 圏 E に相当するモデル図を必要なだけ描きます。この作業では、”Round Trip” が可能なツールが役立つことは間違いないでしょう。
モナド
次は、計算科学における、圏論の代表的な活用例と言われる、モナドについてです。
モナドの定義ですが、

だそうです。上の図の 圏 C は、モノイドです。
圏論を知らない人にとっては、全く珍紛漢紛ですよね。私も完全に理解しているわけではないのですが、要するに代数的な演算や、周辺機器との入出力や、0 で割ってしまうとかの異常を含めた計算効果(computational effect)の基盤となる圏のようです。最近では、プログラミング言語の定義でも考慮されているようで、代表的なものでは、そのものずばりモナドが出てくる、Haskell が有名。
モナドの基本を踏まえて、Maybe Monad とか、State Monad、Graph 上の Monad、Set 上の Monad、List 上の Monad 等、対象の種類などによって様々な Monad が考案されて活用されているようです。
概念モデリングでは、ドメインオペレーションと状態アクションをきちんと定義する基盤になるはずで、”みんなの圏論”の第7章 7.3 モナド は正に、使えそうな例がたくさん載っています。ただし、概念振舞モデルのアクションはデータフローモデルベースなので、その辺りがどのように圏の定義・定理とかかわってくるのかが、私の興味のポイントです。
”概念振舞モデル”では、実行セマンティクスも含め、諄いくらいの解説をしているので、圏論、モナドに詳しい方、考え方についてサポートしていただけるとありがたい。
私が読んだ書籍の中で、”圏論入門 Haskell で計算する具体例から”という本があります。この本、とても詳しく書かれていて、圏論を体現した Haskell を使った具体例が豊富なのは良いのですが、なにぶん、私が Haskell に馴染みがないため、なかなか理解するのが難しいというのが本当のところです。普段よく使っている C# とかで、例を書いてくれると嬉しいなぁ…なんて思いながら、探したら、Tasks, Monads, and LINQ - .NET Parallel Programming (microsoft.com) というブログを見つけました。やはり、関数型の要素が取り入れられた、LINQ 等は モナド を意識しているっぽいです。async 系もそうなんでしょうね。go は、一部取り入れられていたり、Rust は対応してはいないとしながら、何人かの人が モナド を取り込む方法を模索しているようです。
モナドの応用の話でよく出てくるのが、ゼロで割り算をしてしまうような、実行の失敗も含めたコードの扱いの例について思うところがあるので、ちょっと書いてみようと思います。”圏論の道案内”P248に、「そんなの分岐をかけばいいじゃん」的な記述があり、それに続けて
…プログラムの連鎖が一つや二つなら良いが、もしこの後にもプログラムがいくつも続いていると非常に厄介だ。それぞれのプログラムで入力を受け取るごとに「これは失敗かもしれない値だ」と意識し続けるのも面倒だし、分岐を何度も書いていくのもコードの見た目を損なう。
確かにな。大体そういう煩雑なのはバグの温床になって困るんだ。
…
との文面があります。確かにその通りで、私の様な奇人(奇特な人)ではなく一般のソフトウェア開発に携わってプログラムコードを書いている人たちの中で、「プログラムコードを書くことだけがソフトウェア開発だ」と思っている人達にとっては、正に真実であり、制御ロジックの本筋に関係ない値のチェックや分岐は煩わしいものでしかないのでしょう。
しかし、この問題について、概念モデリングと変換による実装によるシステム構築のやり方では、ちょっと違った見方をします。
ドメインオペレーションにしろ、状態アクションにしろ、それらの実行を引き起こす引数は、外部からやってくるものの、引数のデータ型は厳密に定義されていて、アクションを構成するロジック要素(データフローなのでバブルを意味する)が参照するのは、概念情報モデルで厳密に定義されたデータ構造で保持され、関連付けられたデータ群だけです。例えば、概念クラス A の概念インスタンス a をアクションで作る場合も、その概念クラス A と他の概念クラス B との間に1対1の Relationship R1 が定義されている場合、他の概念クラス A の概念インスタンスとのリンクがない 概念クラス B の概念インスタンス b が一つ存在しなければならない、つまり、概念クラス A のインスタンスを作る場合は、一連のアクション(ドメインオペレーション、状態アクション)が完了するまでに、新たに一個の概念クラス B の概念インスタンスを作って R1 のリンクを張らなければならないという制約が存在するという事です。逆に言えば、アクション上で、ある概念クラス A のインスタンスを一個参照した場合、R1 でリンクされた概念インスタンス B のインスタンスが必ず存在する事が保証されているので、アクションにおいて、リンクされたインスタンスの有無をチェックする必要はないという事になります。加えて、概念インスタンスの特徴値は、必ず値を持たなければならないので、そのチェックも必要はありません。
つまり、バブルが受け取る入力は「失敗しない値」が基本になる訳です。もしそれが失敗するかもしれない値だとすると、データ群は、現実の世界(圏 W)に一対一対応するはずなので、現実の世界、つまり、ビジネスや制御自体が何らかの欠陥を持っているという事になります。概念モデリングの過程で、そんな欠陥を見つけたら、そのままモデル化するのではなく、ビジネスや制御の問題として、その欠陥を排除するのがやるべきタスクでしょう。
また、保持されているデータ群は言ってみれば、現実世界全体の状態を表しているとも言えます。概念モデリングでは概念クラスに紐づいた状態モデルで状態遷移が定義されているので、状態アクションを記述する場合は、プログラムコードだけで記述する時に比べて気にしなければならない条件等は劇的に低減されています。
そんなわけで、アクションを記述する時は、プログラムコードだけでシステムを開発する時に比べると、モナドの恩恵を感じる場面は少ないように思えます。
一方で、”変換による実装”で概念モデルからプログラムコードへの変換の仕組みを作るときには、モナドは、プログラムコードだけでシステムを開発する時に比べると、より多くの恩恵をもたらしてくれるように思われます。何故なら、モナドを基に定義されたプログラム言語は、そうでない言語に比べて、同じ処理をより少ない行数で記述する事が可能になるので、変換ルールもより少なくて済むからです。生成されたコードに関する、本筋の処理に関係ない条件判定等のコードを生成しなくて良いという特性は、圏 T の間違いを減らし、変換の仕組みを作る労力の削減に寄与します。
概念モデリングの状態モデルでは、”Can`t Happen”という遷移が定義できます。これは、ある概念インスタンスが、ある状態にあるときに、現実の世界では絶対に発生しないだろうと考えられる事象が発生したことを意味します。たとえば、
”ロボットが電源 OFF の状態あるのに、動作完了という事象が発生した”
というような状況を明示的に定義するのに使います。
「概念モデル上では起きえないのに、何故記述するの?」と疑問に思う人がいるかもしれません。
記述した概念モデルを”変換による実装”でプログラムコードに変換し、そのコードをコンパイル&ビルドして動かしている時、あるいは、モデル図を基に人手でシミュレーションしている時、に Can’t Happen が発生したとします。このとき考えられるのは、
”実行プラットフォーム上でメモリ不足や通信エラー、HW 障害による誤動作が発生している”
という事です。人手でシミュレーションしている時は、”シミュレーションしている内に人が間違えた”ですね。
こうなってしまっては、プログラム上で保持しているデータの正確性や一貫性は保証されず、その後の動作も保証できないため、直ちにシステムを停止、あるいは、停止する為の手段を起動しなければならないでしょう。
その辺りの仕組みは、アプリケーションの概念モデルに書き込むのではなく、異常状態ハンドリングというようなドメインと、圏 T で対応することになります。
勿論、モデル作成者が誤解していて、本来なら起こりうるのに、起こりえないと勘違いしている場合もあるので、そちらの確認もしなければなりませんが。
生成 AI 系との関連
このコラムの冒頭で言及していた、生成 AI による、モデルの自動生成の件について、現時点での見解を記しておきます。
この半年近く、沢山の圏論に関する書籍を、結構何度も何度も読み返してきました。前にも書きましたが、これ、LLM を使った学習の過程みたいだな…と感じています。ChatGPT や Open AI は、基本的にはニューラルネットワークで構成されているので、学習した知識は、ニューラルネットを構成するノード間の重みづけの集合で表現されているはずです。

この重みづけの集合は、ざっくり言うと圏で表現できるはずです。
これは多分どんな圏であれ間違いないと思われるので、考察を続けます。
知識体系を表現できる olog の圏とは、圏同値の関係にあるといえるのではないか。
もし、圏同値であるとしたら、何らかの自然変換を用意してやれば、ニューラルネットが保持している知識体系を可視化(図表現でもテキスト表現でも可)できるのではないか。
もしできるとしたら、問題になるのは、保持されている知識体系が、圏 C と 圏 I のどちらなのか?あるいは別の圏なのか。
多分、1. までは確実にそうだろうなと予想してますが、3. まで出来るとして、圏 C なら、私の当初の目的である、”現実世界の情報から概念モデルを自動生成する”は、生成系 AI に現実世界の情報をたらふく食わせて学習させた後に、何らかの自動変換を使って、概念モデル一式を取り出すことができて、私の野望は達成という事になって、めでたしめでたし、です。
しかし、それが 圏 I の場合は、単に、概念インスタンスやリンクの候補になるオブジェクト候補を挙げてくれるだけのアシスタント的な役割しか担えない、という事になります。圏 C でも 圏 I でもない場合は、もうお手上げだ。
こんな観点で、ニューラルネットを研究している人、いないよね…
最近読んだ本、思い出せないのう…、ではなく”思い出せない脳”の第4章には、
脳は記憶を整理する時に、「類型化」を行っています。
類型化とは、複数の物事の中から共通の項目を取り出してまとめることです。タイプ分け、カテゴリー分け、パターン訳は全て類型化です。脳は、似たようなものをグループにして記憶を作っているのです。
と書いてあります。概念情報モデルの概念クラスや Relationship 抽出は、正に類型化の一つですね。という事は、人間の脳味噌には、圏 I のオブジェクト群だけでなく、圏 C のオブジェクトも混在している事になります。
人間の脳味噌をモデル化したニューラルネットも、同じような動きをするなら、圏 C、圏 I が混在して存在する可能性はゼロではないでしょう。
概念モデリングに関連しそうな圏
以下、私が読んだ書籍で概念モデリングに関連しそうな部分をリストアップしておきます。
みんなの圏論
2.3 オントロジーログ
4.5 データベース:スキーマとインスタンス
5.4 圏とスキーマの同値性
活躍する圏論
3 データベース:圏、関手、普遍的構成
4 協調設計:プロ関手、圏化、モノイダル圏
5 信号流れ図:prop, 表示、証明
6 電気回路: ハイパーグラフ層とオペラッド
7 振舞の論理:層、トポス、内部言語
圏論の歩き方
4 プログラムの意味論と圏論
5 モナドと計算効果
6 モナドのクライスリ圏
7 表現を<表現>する話
14 表現論と圏論化
圏論の基礎
ぜんぶ
最後に
以上、長々と書いてきました。
最後まで読んでくれた読者がいたら、あなたは神!
私の圏論の旅はまだ始まったばかりな感じです。細かいところは間違っている部分も多々あるかとは思いますが、大筋では外してないかなとは思っています。
翻って見れば、Shlaer-Mellor 法を理解して使いこなせるようになるまで、実に7~8 年かかったことを思えば、半年ぐらいまだまだって感じです。
しかし、若い時のその年月と、今の年齢でのその年月はやはり差があって、なるべくなら効率よく習得したいものだと思ってます。
その為には、
プロの助けが必要だ
につきます。このコラムをきっかけに、私が読んだ書籍の著者の皆さんとのつながりができ、判らない事があったら気軽に聞ける関係になれたらいいなぁ…と切に願ってます。
また、今回の文面は、多分、プロから見ると、非常に怪しげな説明が多々あると思います。その辺も、建設的なコメントで、ビシバシ指摘してくれるとありがたいです。
皆様、是非!
