できることとできないことを見極める
「自分に何ができて何ができないのかを認識する」
これが分かっているようで、実践できていな人が多いようです。私も多分出来ていません。
例えば、よく言われるのが「人間関係」。
最近は、「ダイバーシティ」という言葉とともに、
他人を「そういうもの」と受け入れる事が大事
という考え方が浸透してきています。しかし、実際に自分の人との接し方を考えてみると、どうしても
「他人の考え方を変えようとしてしまう」
ことは無いでしょうか。
人の本質は、そう簡単に変わるものではありません。人間の感情は、「大脳辺縁系」と言われる、進化的に古い脳の部位が司っていて、そこに刻み込まれた生存本能に大きく影響されるからです。
表面的な行動は、一時的には変えることが出来ると思います。しかし、感情で納得していない部分があると、歪みを抱えたまま関係が続くことになり、時に大きな問題になる事があります。
一方、人間は「大脳新皮質」が非常に発達しており、時に「辺縁系」で生まれた感情も変えてしまう程の力があります。しかしそれは、あくまで
「自分で深く納得した考え」
によるものだけです。見たり聞いたりしたことだけでは、そこまでの力はありません。
だから、人間関係に悩みがある場合、根本的な解決方法は、
①自分の考え方を変える
②相手を受け入れて割り切る
③関係を築く人を変える
しかありません。これなら、自分で何とかできる話です。
そもそも、ほとんどの悩みというのは、
「自分ではどうにもならないことを、どうにかしようと考えている」
場合が多いです。
「不景気で仕事が減り、生活が苦しい」
というのも、「不景気」という社会状況は、政治家にでもならない限り、自分ではどうにもなりません。なので、
「現状でニーズが高い、または景気の影響を受けない仕事を探す」
だったり、
「その仕事に就くためにスキルを高める」
などの行動を起こすしかありません。
「仕事で結果が出ない、または終わらなくて辛い」
というのも、仕事の結果や進め方の大部分が、他人や環境に依存した形になっていると、自分では解決できない問題です。それが悩みになるのであれば、
「どうしたら、自分がコントロールできるような仕事の仕方ができるか」
を考えたり、さもなくば
「仕事自体を変える」
事が、解決の選択肢となります。
つまり、問題解決をしようとした場合、まずその問題について
「自分で解決できる内部要因と、自分ではどうにもならない外部要因」
の部分に仕分けするのが第一歩となります。
ということで前回は、微分方程式を立てる話でした。
●解き方の意味を考える
微分方程式の解き方については、分かりやすい教材が色々ありますし、そもそも記事にしたところで面白くないので、触れないつもりでした。
しかし、紹介されている解き方は、そういう決まりであるかのように、
「斉次方程式の一般解と非斉次方程式の特解の1つを求めて、足したものが一般解になる」
としか書かれていないものが多いです。
多分、初めて学ぶ人の多くが、
「特解?一般解?斉次方程式?」
となって、ただ解法だけを勉強させられるという、辛い修行に挫折してしまうのです。
なので、せめてその意味だけでも考えてみようと思い、今回はやっぱり解き方について考える事にしました。
●斉次・非斉次方程式の意味
「斉」とは、「一斉」の斉で、「揃っている」という意味があります。
何が揃っているのかというと、式の「左辺」と「右辺」の、
「定数項を除く、各項の未知関数の次数」
です。例えば、関数 "x = f(t)" に関する微分方程式で、定数 "a1", "a2", "b1", "b2", "c1". "c2" として、
a1(d^2 x / dt^2) + b1(dx / dt) + c1 x = a2(d^2 x / dt^2) + b2(dx / dt) + c2 x
という微分方程式は、左辺と右辺の
"d^2 x / dt^2" (2回微分)
"dx / dt" (1回微分)
"y" (そのまま)
の、それぞれの項の次数(何乗になっているか)が同じですね。なので、これは「斉次方程式」という事になります。
斉次方程式は、左辺に右辺を移項すれば、
(a1 - a2)(d^2 x / dt^2) + (b1 - b2)(dx / dt) + (c1 - c2)x = 0
というふうに、
未知関数を含む多項式 = 0
の形にできます。
一方、方程式の中に「定数項」や「"t"を含む項」があり、"p", "q" を定数として、
a(d^2 y / dx^2) + b(dy / dx) + cy = pt + q
などという形になっている場合は、「非斉次」になります。
まず斉次方程式が何を表しているかを考えてみます。前回の、「バネと錘」の例(下図)で、
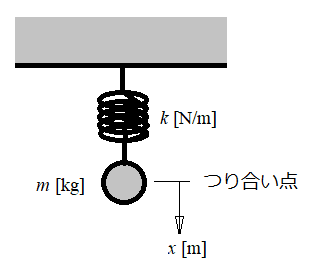
m(d^2 x / dt^2) = mg - kx
という方程式に対して、
関数 "x(t)" を含んでいない項 "mg" を "0"とした
m(d^2 x / dt^2) + kx = 0
という斉次方程式を解くことになります。
"mg" は「重力による外力」を表す項ですから、これは、
「バネ定数と錘の重さで決まる、系の運動特性」
(つまり、バネの復元力による往復運動)
を考えることになります。
それに対し、"mg" を入れた「非斉次」の方程式の特解は、
重力がかかった時のつり合い状態でのバネの伸び
(つまり、外力の作用による平均値の変化)
を考えることになります。
●システムの特性と外部入力に分ける
電気回路で考えると、よりその意味が明確になるでしょう。
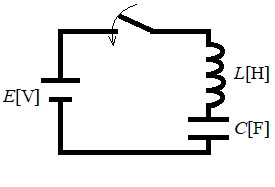
上図も前回考えた電気回路ですが、これは、
「電源電圧 "E [V]"」
と、「コイルのインダクタンス "L"」と「コンデンサの静電容量 "C"」の
「リアクタンスによる逆起電力」
とのつり合いを考えて、「コンデンサの電荷 "q"」についての微分方程式
E = L(d^2 q / dt^2) + (1/C)q
を考えたのでした。
しかし、この回路は "L" と "C" 振動回路です。つまり、コンデンサとコイルの電圧は、瞬間的には変動しています。
その「電荷の変動成分」、つまり
「交流成分」は、回路の定数で決まるシステム特性(振幅や周波数)
となり、
「直流成分」が、外部入力である電源から印加した電圧による電荷
となります(下図)。
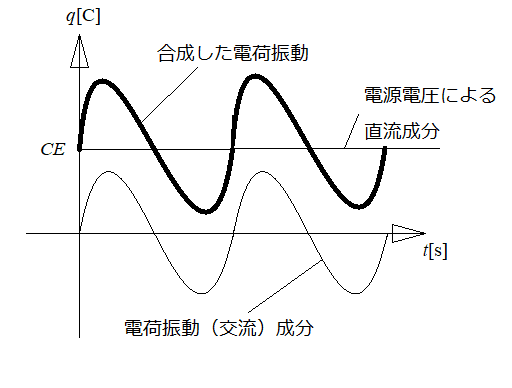
つまり、この微分方程式を解く中で、斉次方程式
L(d^2 q / dt^2) + (1/C)q = 0
の一般解を求める過程が
「交流成分を求める過程」
であり、非斉次方程式
L(d^2 q / dt^2) + (1/C)q = E
の特解を求める過程が、
「直流成分を求める過程」
という事になります。
そして、これらの解を足し合わせた
一般解 + 特解
が、最終的な微分方程式の解になるのは、
「システム特性」による変動成分
と、
「外部入力」によるオフセット成分
を重ね合わせている事になります。
まとめると、「微分方程式を解く操作」の物理的意味は、
「時間的に変化するシステムの出力」
を、
「システムの特性」と「外部入力」
に分けて考えて、後から重ね合わせる操作
をしているという事です。
●「線形」の場合しか重ね合わせられない
しかし、これで解が求まるのは、あくまで
「微分方程式が線形で表現できる場合」
のみです。「非線形」ではこのようなことが出来ません。
(2乗の項などが入ると、単純な足し算にならないですね。)
だから、何か現象をモデル化する場合、
「線形とみなせる部分を取り出して近似する」
というのが一つのポイントになったりします。そしてこの
「線形とみなせる範囲」
を見誤ると、大きな誤差が出て問題になったりするわけです。
ちなみに、非線形現象を解析するのは、「カオス理論」になります。
ということで、次回こそ、ラプラス変換の話に入ろうと思います。
