「システム」と「系」は違う

　システムキッチン、システム手帳、システムエンジニア等。

　「システム」って言葉が良く使われます。「システマティックな考え方をしなさい」とも言いますよね。

　　何となく「便利そう」、「使いやすそう」、「仕事できそう」ってイメージでしょうか。でも「どういう意味？」と聞かれると、困っちゃう人も少なからずいるのではないでしょうか。

　システムは、日本語に直訳すると「系」です。「家系ラーメン」とか「渋谷系」（最近言わないな）なんかの系です。

　これを考えると、ますますわけわかんないですね。私も、大学の熱力学でこの訳を知ったとき、非常に頭をひねったことがあります。

　もっとわかりやすい例で言うと、「系統」とか「系列」の系ですよね。つまり、何らかのルールに従って関連付けられた、一つの集合の事と言えます。

　そういう意味では、家系や渋谷系も何となくわかります。でも、「家システム」とか「渋谷システム」はなんかちょっと違いますね。

　この違いは、「システム」と言った場合は、全体として何か機能する事が期待されているからだと思います。つまり、ある集合の中の要素同士が何らかの役割を持ち、それらが関連し合って一つの機能を実現する、そのような集合をシステムと呼ぶのだと考えます。

　あまりいい例ではないかもしれませんが、CPU、メモリ、ハードディスクなど、これらは「コンピュータ系」の部品と言えます。しかし、この部品を集めただけでは「コンピュータシステム」とは言えません。

　これらが組み立てられて配線されて、動くようになってやっと「システム」になるわけです。

　システムキッチンも流しやガス台がひとまとまりに組み立てられて、「システム」になっているという意味ですね。（そもそもキッチンがシステムになのだと思うのですが、そこはイメージ商法なのでしょう。）

　システム手帳も、ただ日毎にメモを書くのではなくて、例えば長期計画を書く欄とか、細かいスケジュールを書く欄とか、ToDoリストでタスク管理をする欄などに分かれています。そして、それぞれが別々の役割をもって、全体でプロジェクト管理に使える「システム」となっているのです。

　システムエンジニアは、まさにシステム（機能する仕組み）を作ったり、それを管理したりする仕事です。（しかし、IT系だけが「システムエンジニア」と呼ばれている理由はよくわかりません。プラントエンジニアなんか、もっと大きな「システム」のエンジニアなんですけどね。）

●熱力学の「系」

　ということで、熱力学のシステムの話です。

　エントロピーの話をしたときに、

「エントロピーの増大の法則を言うには、その系がどんな系であるかも示さなければならない」

という事を言ったのですが、その「系」について説明していなかったので、ここで説明します。

　いろいろな熱現象や熱サイクルを考えるには、

一体どのような系（システム）で考えているのか

ということをはっきりさせないといけません。例えば、

（以下問題）

1atm の部屋の中で、100cc の沸騰したお湯の中に、10g の氷を入れた。

水と氷の密度をともに 1g/cc とし、氷の融解熱を 79.7cal/g とすると、十分時間が経ったとき水は何℃になるか？

（問題終わり）

という問題があったとします。普通に解けば、

（以下解答例）

100cc の沸騰したお湯の熱量は、（0℃ を基準に）

1cal/(g*℃) * 100g × 100℃ = 10000cal

10g の氷が溶けるのに必要な熱は、

79.7cal/g × 10g = 797cal

氷が溶けてできた水は 0℃ だから、その熱量は 0cal

氷がとけた後の水の総量は、110g だから、

(10000 - 797)cal/(110g * 1cal/(g*℃)) = 84℃

（解答終わり）

です。しかしこれは、

暗黙のうちに「水」と「氷」の系で考えている

事になります。

　もし、この系として「部屋（20℃とする）」まで含めたら、

十分時間が経てば室温と平衡になる

はずなので、

「水は 20℃ になる」と言わなければならない

わけです（下図）。（なんかひねくれてるみたいですけど。）

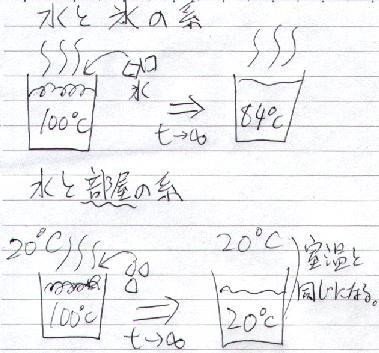
　このように、

物理現象を考えるときに対象とする物質、物体、場などからなる全体

を

「物理学系」または「系」

と呼びます。「系」に含まれないものは「外界」と言います。熱力学では、外界とやりとりするエネルギー形態によって主に四つの系に分けられ、当然系によって使える条件も違ってきます。

　「系」と「外界」が直接やり取りするエネルギー形態には、「物質」、「熱」、「仕事」の三つがあります。どの系が、外界と何をやり取りできるのかを、以下の表と図にまとめておきましょう。

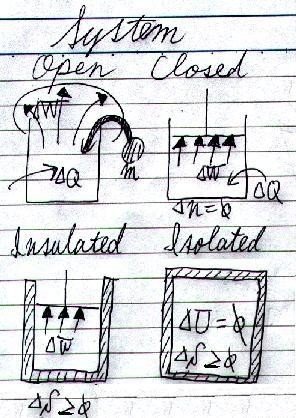
　「開いた系」は、主に

大気圧下での相変化や化学反応

の場合です。

●系によって変わるエネルギー保存則（熱力学第一法則）

　さて、ここで熱力学第一法則である「エネルギー保存則」と系の関係を確認します。物質の出入りが無ければ、これは実に簡単な形で書けます。

　系が持つエネルギーを「内部エネルギー」と言い、"U"で表わすと、

dU = δQ + δW --- ( 1 )

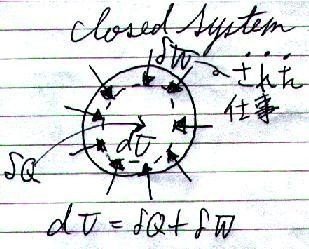
　尚、ここで熱"δQ"、仕事"δW"はともに、

"dU"が「増加となるほう」

を正とします。

　そして、変化が「準静的」なときこれらは、温度"T"、エントロピーを"S"、圧力を"P"、体積を"V"として、

δQ = TdS --- ( a )

δW = -PdV --- ( b )

と書けるので、( 1 )式は、

dU = TdS - PdV --- ( 2 )

となります。これは、「閉じた系」の熱力学第一法則の式です。

　「断熱系」では

δQ = 0

であり、( 2 )式は

dU = - PdV

となります。「孤立系」では、熱や仕事の出入りはなく、

δQ = 0, δW = 0

のため、

dU = 0

となります。

　一方、「開いた系」では物質の出入りもあるため、ここでは扱いませんがもっと複雑です。このように、熱力学第一法則は、系によってその中身が大分変ってくるという事が分かったと思います。

●改めて状態量について

　さて、( 1 )式と( 2 )式を比べると、まず

"δW"と"PdV"が異符号

となっています。体積が増えると、その分

「外界」に仕事をした

ことになるので、

内部エネルギーを「減らすほう」

になります。

　もう一点、( 2 )式は

「状態量」だけで表わされている

ので、途中の経路に依りません（わからない方は、以下の記事

も参照して下さい）。

　つまり、内部エネルギーは、（準静的過程で）状態量であるわけです。状態量であるという事は、

何らかの関数で表現できる

という事でもあります。次回は、準静的過程で状態量がどのような関数になるかを、ちょっと考えてみます。

■ついでに示強変数と示量変数

　上の記事で、

「示強変数」と「示量変数」についてお話しします

と言っておいて忘れていたので、ここでお話しします。

　( a )式と( b )式を比較してみると、

"P"に対して"T"

"dV"に対して"dS"

が対応しています。

　( b )式で、「体積"V"」は例えば、

（1L（リットル）の系）+（2Lの系）=（3Lの系）

と単純な足し算になります。こういう量を、「示量変数」と言います。エントロピーも示量変数です。

　つまり、エントロピーは「系の大きさ」に関係した量であることが分かります。

　それに対して「圧力"P"」は、

（1atmの系）+（2atmの系）

は、「3atmの系」にはなりません。

　こういう足し算にならない量を、「示強変数」と言います。「温度"T"」も示強変数です。

　「示強変数」、「示量変数」などの概念がいつ確立されたのかは調べられていません。多分、解析的手法を発達させた、マクスウェルあたりが言いはじめたんじゃないかと思います。

　熱力学では、「エネルギー」という目に見えない量を、その性質によって区別して表わします。

　力学や電磁気学などの、比較的物理的意味を掴みやすい分野では、こういう概念は必ずしも必要になりません。しかし、イメージのつかみにくい変数が沢山出てくる熱力学では、このような「変数の分類」によって性質を理解することが、有効になる場合が多々あります。

　ちなみに英語では、「示量変数」は"extensive variable"、と言います。多分、量に比例する事を指して「伸縮性の」という言葉を当てはめたのだと思います。「示強」はその反対の"intensive"になります。

　科学用語は、英語の方が意味が分かりやすい場合が、往々にしてあります。