
美しくて便利
「世の中で一番、美しさと便利さを兼ね備えたものを挙げよ。」
と言われたら、私は間違いなく
「オイラーの公式」
を挙げます。
カバーの図に示したのものなのですが、
![]()
という式です。
左辺は「指数関数」、右辺は「三角関数」で、
指数関数の変数を「虚数に拡張」
すると、これらが結び付いてしまうという、何とも不思議な式です。
世間一般では、この式で
θ = π [rad] (180°)
を代入した、
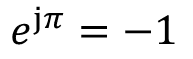
という式が有名です。さらに、"-1" を移行すると、
e^jπ +1 = 0
という、数学上重要な、
e:ネイピア数
j:虚数
π:円周率
1, 0
という数が全て出てくるという理由で、
「一番美しい数式」
なんて言われたりしています。
しかし、その本質としては、
「指数が虚数になると回転になる」
ということが重要です。
●オイラーの公式を使うと何がうれしいか
前回の複素数の記事で、
「極形式」
というのがありました。すなわち、複素数 z が「直交形式」で
z = 3 + j 3√3
と書けたとすると、その「極形式」は、
z = 6∠60°
となります(下図)。

そして、2つの複素数の掛け算をするとき、例えば
z1 = 2 + j 2 = 2∠45°
z2 = 2√3 + j 2 = 2∠30°
という複素数に対して、
z1 * z2
·したとき、その積の大きさと偏角は、
(2 * 2)∠(45 + 30)° = 4∠75°
という計算ができるわけですが、これは、
2e^j(π/4) * 2e^j(π/6) = 2*2 e^j(π/4 + π/6) = 4 e^(5π/12)
※角度の単位は[rad](ラジアン)で、
45° = π/4 rad
30° = π/6 rad
75° = 5π/12 rad
です(下図)。

という指数計算になるからです。
掛け算なら、まだ直交形式で計算しても、それほどの手間ではありませんが、これが割り算になると、もっと有難みがわかると思います。例えば、
z1/z2 = {2e^j(π/4)}/{2e^j(π/6)} = (2/2){e^j(π/4)}/{e^j(π/6)}
=1*e^j(π/4 - π/6) = e^j(π/12)
と、大きさの割り算と角度の引き算で計算できます。
そして何より、交流回路でこれを使う一番のメリットは、
「電流や電圧の大きさと位相がどうなるか、一目でわかる」
ということです。
●実際に計算してみる
それでは、前回の回路をもう一度、今度はオイラーの公式を使って、「インピーダンス(交流の抵抗)」から電流を求めて、さらに電力を求めてみたいと思います。

コイルのリアクタンス:j6 Ω
抵抗:2√3Ω
が、「並列」に接続されているので、インピーダンスは
Z = (j6 * 2√3)/(j6 + 2√3)
分母を有理化すると、
Z = (j12√3)(j6 - 2√3)/{(j6 + 2√3) (j6 - 2√3)} = (-72√3 - j72)/(-36-12) = (3/2)√3 + j3/2
です。
これを指数関数で表現すると、偏角は、
∠Z = arctan{3/2 ÷ (3/2)√3} = arctan(1/√3) = 30°
なので、
Z = 3e^j(π/6)
となります。
従って電流は、オームの法則で、
I = V/Z = 100 / {3e^j(π/6)} = (100/3)e^j(-π/6)
(※指数は分母に来ると、1/a = a^(-1) とできます)
と求まり、
偏角を表す指数が -π/6
と出てくるので、
「30° 遅れ」
になるということも、オームの法則で求めることが出来てしまいます。
●電力の計算
では、電力はどうかというと、
電力 = 電圧 × 電流
なので、そのまま
100 × (100/3)e^j(-π/6)
としたいところなのですが、ここで一つ約束事があります。それは、
「複素数で電力を計算する場合、電流は共役を取る」
ということです。
「共役」とは、
複素数の「虚数部の符号が入れ換わった」もの
のことで、つまり、
I = 50√3/3 - j50/3 = (100/3)e^j(-π/6)
に対して共役を取ると、
I~ = 50√3/3 + j50/3 = (100/3)e^j(π/6)
となります。
よって電力は、
S = V × I~ = 100 × (100/3)e^j(π/6) = (10000/3)e^j(π/6) [VA]
となります。これを、「複素電力」と言います。
これが表している事は、
①皮相電力の大きさは、10000/3 [VA] である
②電力の力率角は π/6 [rad] (30°) 遅れである
(「角度が正の値なのに遅れ?」
と思った方がいるかもしれませんが、先ほど
「電流について共役を取る」
としたことが関係しています。詳しくは、機会があったら解説します。)
ということになります。
ところで、これは直交形式で表すと、
S = 5000√3/3 + j 5000/3
となりますが、この
実数部の 5000√3/3 W
が「有効電力」
虚数部の 5000/3 var
が「無効電力」
となります。
有効電力は、
仕事として消費される電気エネルギ
で、無効電力は、
「誘導負荷(コイル)」や「容量負荷(コンデンサ)」で一旦蓄えられるが、最終的に電源に帰っていくエネルギ
となります。そして、電源設備としては、有効電力と無効電力を含んだ「皮相電力」を出力できる容量が必要となります。
無効電力が大きいと電力に無駄が出ます。電気料金はあくまで「有効電力」の消費に対して請求されるものですが、大きい電力を消費する需要家では、無効電力の大きさによる基本料金の割引や割増があったりします。
複素数を使わない計算では、有効電力と無効電力を個別に求め、ベクトル図を描いて皮相電力を求める必要がありました。しかし、複素数を使うことで、これらが
計算だけで一緒に求める
ことが出来ます。
このように、オイラーの公式は、ただ数学的に美しいというだけでなく、
電気回路の計算を非常に見通しの良いものにした、実用的な公式
でもあるのです。
