タイミングが大事
「伝え方が9割」
というビジネス本が売れてますね。
でも、営業としてお客様と話をしたり、技術者として人に説明をしたり、教員として学生に教えたりした経験をもとに言わせてもらうと、
「伝え方をいくら工夫しても、意図した通りに伝わらない事が多い」
というのを、まず肝に銘じておく事だと思います。さらに、むしろ実感としては、
「伝えるタイミングが9割」
でした。
つまり、何か人に言葉を伝えようとするときに、
①まずは自分が「伝えたい」という意識になっているか
②伝えるのに必要な知識など十分に準備できているか
③相手がその話を聞きたい状況か
④相手の聞く態勢が整っているか
という事を最低チェックします。もちろん仕事ですから、これらの条件が揃っていなくても、話はしなければなりません。
しかし、少しでも条件が満たされるタイミングを選び、また状況を作ることで、ちゃんと理解してもらえる事が多くなります。
そういえば、かつてドイツの独裁者だったヒトラーは、演説で大衆の心理を掴んでいたと言われていますが、演説の「時刻」が重要だったそうです。
ヒトラーが労働者に向けて演説を行ったのは、午後8時過ぎ。仕事を終えて疲労し、判断力が鈍っている時間を狙っていたと言われています。
また、ドイツの4~10月の日没も、午後8時頃。この夕方から夜にかけての時間帯は「逢魔時」とも言われ、特に人間の思考力が低下し、交通事故なども起こりやすいと言われます。そういうタイミングを狙って、ヒトラーは印象的なフレーズを力強く繰り返し、人心を掌握していたのです。
●交流の電気が発生する仕組み
と長々と前置きをしたところで、急に電気の話です。前回は、交流回路で使う「複素数」について考えました。
複素数は、普通の実数と異なり、「複素数平面」上での「長さ(大きさ)」と「偏角(角度)」を考えるという事でした。この偏角が何故必要になるのかという話を、まず考えていきたいと思います。
電気は、電流や電圧の変化の仕方から、「直流」と「交流」に分類されます。
「直流」は、電池のように、
電源の「"+" と "-" の極性」が固定されていて、電気の流れが「+から-の一方通行」
という事になっています。一方、「交流」は、
電源の「極性が交互に入れ替わる」ため、電気の流れる「方向が周期的に変化」
します(下図)。

例えば、電力会社からコンセントに供給されている電気は「100Vの交流」ですが、
「関東の電気は 50Hz(ヘルツ)で、関西は 60Hz」
というのを聞いたことがあると思います。その違いの理由はここでは置いといて、関東では
1秒間に 50回、+と-の方向が入れ替わっている
という事になります。
何でそんな電気が送られているのかというと、発電機が「電磁誘導の法則」を利用して発電している事に由来します(下図)。

図のように、右のコイルに左の磁石を近付けると、
「コイルを貫く磁束が変化」
します。すると、コイルにはその
「磁束の変化に逆らうように電流を流そうとして、誘導起電力が発生」
します。その起電力を利用して、発電を行っています。
これは、
「コイルに対して磁石が運動して、磁束が変化」
しないと発電できませんので、安定して電気を送るには、
「磁石を常に動かしておく」
必要があります。図のように「直線的」に動かしてもいいのですが、
継続的に発電するには無限の距離が必要
になります。なので、実際には
磁石を回転させて、磁束を継続的に変化
させています(下図)。

但し、「回転」するため
磁石の極性が逆転
します。だから、
起電力の方向も逆転
することになり、交流の電気となります。
ちなみに、発電に必要なのはこの「磁石を回転させるエネルギ」であり、それに
「水車」を使えば「水力」
「燃料を燃やして」お湯を沸かして、蒸気タービンを回せば「火力」
「風車」を使えば「風力」
「核分裂」の熱でお湯を沸かして、蒸気タービンを回せば「原子力」
になるわけです。
(さらに余談ですが、太陽光や燃料電池は継続して「直流」が発生するもので、これらとは原理が全く異なります。)
●交流電圧の変化を定量的に表す
このように交流回路では、
ある瞬間の電流や電圧が、時間的に変化
しています。そしてその変化は、
「磁石の回転運動」
になります。
交流電圧は、「コイルの誘導起電力」ですが、これは、
「回転する磁石」の作る磁束
のうち、
「ある方向の磁束」の変化
を捉えている事になります。
磁石の回転速度は、1秒あたりの回転の角度である「角速度」で表せますが、その「ある方向の磁束」は、「三角関数」を使って、下図のように表現できます。
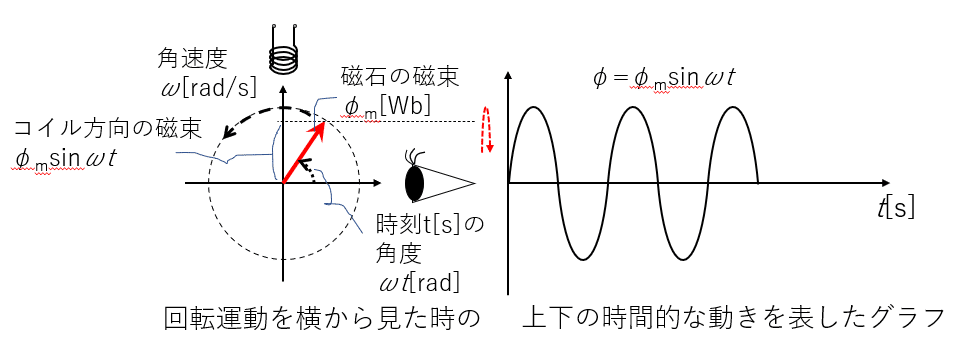
そして、その変化から得られた電圧も、三角関数を使って、
V = Vm sin ωt
という風に表せるわけです。
(正しくは、変化だと微分になるので cos になったりしますが、ここではとりあえず「三角関数になる」という事だけおさえてください。)
この変化は、グラフを見てもわかるように「周期性」のある変化ですが、
「1周期中のどのタイミングか」
によって、その時の電圧が決まります。このタイミングの事を、「位相」と言っています。
位相は、もともとは回転角度からきているので、単位も角度と同じで、
「" ° " (度)」または「"rad"(ラジアン)」
で表されます(下図)。

例えば、50Hzの交流100Vの電源の場合、ある位相(タイミング)の電圧は、
v = 141sin(100πt)
と表す事ができます。50Hz ということは、1秒間に50回入れ替わるという事ですから、逆に1周期の時間としては、
1/50 = 0.02 sec
となり、0.02秒ごとに同じ電圧が繰り返し現れることになります。そして、時間ごとの電圧の値を見ると、例えば以下の図ようになります。
(実際に式の t に値を代入して、関数電卓などでその値になるか確かめてみてください。)
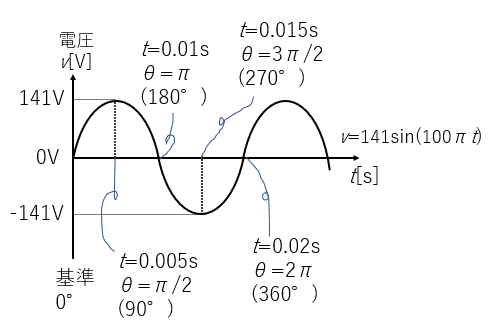
t = 0 s の時:電圧 v = 141 sin(100×3.1416×0) = 0 V
t = 0.005 s の時:電圧 v = 141 sin(100×3.1416×0.005) = 141 V
t = 0.01 s の時:電圧 v = 141 sin(100×3.1416×0.01) = 0 V
t = 0.015 s の時:電圧 v = 141 sin(100×3.1416×0.005) = -141 V
t = 0.02 s の時:電圧 v = 141 sin(100×3.1416×0.02) = 0 V
大分間隔は荒いですが、確かに電圧の+と-が入れ替わっていて、0.02 秒でもとに戻っている事がわかります。
●交流回路ではタイミングが大事
実際の電力系統では、電源は一つだけではなく、多数の発電所の発電機が接続されています。その場合、それぞれの発電機のスタートのタイミングが違うと、
電圧の違うものを接続
することになり、
電圧の高い方から低い方に電流が流れてしまう
事になります(下図)。

なので、この
「位相を合わせる」
というのが重要になります。実際に、新たに発電機を連携させるときは、「位相同期検定」というのを行い、同期が取れたら遮断機を投入するという事が行われていたりします。
イメージとしては、大縄跳びが回っている中に、タイミングを合わせて入って一緒に飛ぶような感じです(下図)?
●複素数と交流の関係
ここまでお話しして、やっと「複素数」が出てきます。複素数には「偏角」というものがあるわけですが、この偏角が、交流の位相を考えるのにとても便利なのです。
そして、電気回路には、基本となる「オームの法則」があり、これは、
ある負荷(抵抗)に電圧をかけたときに流れる電流と、その電圧の関係
を表し、
電圧 "V [V]"、電流 "I [A]"、抵抗 "R [Ω]"
とすると、
V = IR
です。
直流回路では、ただ「大きさだけ」を考えればよく、また「コイル」や「コンデンサ」についても、定常的な回路の動きを考える上では、その「純粋な抵抗値」だけを考えれば十分でした。
しかし、交流では「大きさ」の他に「位相」も考える必要があり、特にコイルやコンデンサでは、
「電圧と電流の位相がずれる」
という現象が起こります。なので、
「オームの法則を複素数に拡張する」
という考え方が必要になります。
今回は交流回路についての話が長くなってしまったので、また次回、続きを書きたいと思います。
