先見性とは本質を捉える力なり

　ここのところ、目の前の物事に気を取られて書いた記事が、2つも続いてしまいました。

　日々の話題について何かを述べるのは、やはりお手軽なんですよ。

　「今、目に見えている物事」

というだけでインパクトが強く、なんだか物を考えたという充実感が味わえるんです。しかし、先を見据えた考えというのは、大きな歴史の流れの中で、過去に積み重ねられてきた事実の中からしか生まれてきません。

　現在進行中の物事の中には、学び取れる教訓がほとんどないからです。だから、一時的に満足はしても、何とも言えないむなしさが残ります。

　「学び」の意義は、人間がよりよく生きるための知恵を授かり、それを実践していく事にあります。そのために、人は物事の本質が何なのかを探り、それに迫る努力を続けてきたわけです。

　そして、「本質」に近づけば近づくほど、それは大きな歴史の中で続く、1つの筋であることが分かるのです。

　ということで、熱力学シリーズの続きです。

●気体は膨張しても温度が下がらないことがある

　さて、前回は「エンタルピー」

H = U + PV

という状態量が登場しました。

　「エンタルピー」は1876年、J. W. ギブスが「化学ポテンシャル」や「熱力学的ポテンシャル」とともに考案したものです。しかし、この概念自体はもっと昔から研究されていました。

　1843年、ジュールはこんな実験をしました（下図）。

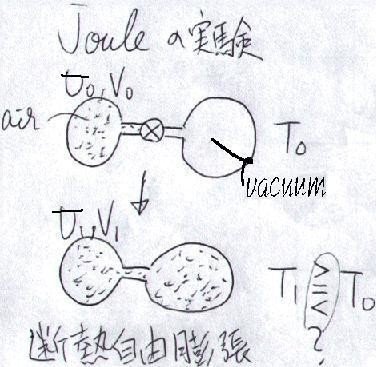
　上図のように、二つのフラスコをコックでつないで、片方に空気を満たし、もう片方を真空にしておきます。コックを開けば、当然空気は真空の方に流れこみ、すなわち「膨張」するわけです。

　さて、このとき空気の温度はどう変化したでしょうか？膨張するので温度は下がるでしょうか？

　答えは"No"です！

　「膨張」と言っても、膨張した先は「真空（P = 0）」なので、膨張による仕事は

PdV = 0

よって、「仕事による温度低下」はありません。この過程を「断熱自由膨張」と言います。実際の実験結果でも、ほとんど変化は見られませんでした。

　ところで、等温過程の時に成立する「ボイルの法則」は、

PV = const.

です。しかし、ボイルがこれを発見した1660年の当時、どうやら彼自身も、厳密にこれが成り立つのかどうか疑問だったようです。

●ジュール・トムソンの実験とエンタルピー

　上の「ジュールの実験」もあまり精度が良くなかった事もあって、その後1854年、トムソンと共に次のような実験を完成させました（下図）。トムソンは1847年、学者ではなかったジュールの「熱の仕事当量」の論文にたった一人注目した人物で、それからジュールとは生涯の友人となったそうです。

　科学の言葉で語り合える、真の理解者だったわけです。こういう関係は憧れますよね。

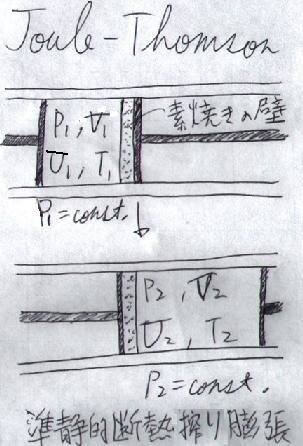
　上図のように、「素焼きの壁」を挟むようにして、2つのピストンを置き、その中にガスを封入します。素焼きの壁を挟んで

片方の部屋を高圧部’（1室）、もう片方の部屋を定圧部（2室）

とします。素焼きの壁は、役割としては「多孔性隔膜」という事になります。

　そして、2つのピストンを同時に動かし、

1室から2室に低圧部に、素焼きの壁を通じて気体を連続的に流す

とします。このとき、

高圧部では"P1"、低圧部では"P2"の圧力を保つ

ように調整します。この間、「周囲とは断熱」されているとします。

　この過程により起こるガスの温度変化

⊿T = T2 - T1

を測定する実験を「ジュール・トムソンの実験」と言い、この過程を「絞り膨張過程」と言います。このとき「エネルギ保存則」はどうなっているか、式を立ててみましょう。

　系は断熱されているので、内部エネルギーの変化は、ピストンを動かす「仕事」のみです。気体が「高圧部で受ける仕事"W1"」は

dW1 = P1dV
↓
W1 = ∫[0;V1]P1dV = P1V1

同様に、「低圧部で受ける仕事"W2"」は

W2 = -P2V2

（マイナスだから「した仕事」になる）

よって内部エネルギーの変化"⊿U"は、

⊿U = U2 - U1 = W1 + W2 = P1V1 - P2V2

となります。

　ここで、上の式をちょっと変形すると、

U1 + P1V1 = U2 + P2V2

だから、エンタルピーの定義より、

H1 = U1 + P1V1

H2 = U2 + P2V2

　つまり、この絞り膨張過程では、

H1 = H2 = const.

となり、

エネルギーが「エンタルピー」の形で保存

している事がわかります。なので、この過程を

「等エンタルピー過程」

とも呼んでいます。

　さて、気になるのはこの実験の結果ですが、

気体によって温度が上がったり下がったり

しました。もっと正確に言うと、

気体の「温度」と「密度」によってその結果が異なり

ました。そこで、この実験で得られた結果をもとに、「ジュール・トムソン係数」という次の量が定義されました。

μ= (∂T/∂P)h

つまり、

等エンタルピー過程での「圧力変化」に対する「温度変化」の割合

です。室温の範囲では、ほとんどの気体は

μ> 0

となり、絞り膨張により温度が低下します。これを、「ジュール・トムソン効果」と言います。

　打撲などでケガをした時に冷やす、冷却スプレーの原理がこの効果を利用しています。高圧のガスが、小さなノズルから出て大気圧下で膨張する際に、ガスの温度が低下します。

　ところが、一般に、ガスがある温度以上になると

μ< 0

となり、温度が上がります。その温度を「逆転温度」と言います。

　「逆転温度」は、酸素（O2）では"49℃"、窒素（N2）では"348℃"とかなり高いのですが、水素（H2）では"-71℃"、ヘリウム（He）では"-173℃"とかなり低くなっています。

　余談ですが、このジュール・トムソン効果は「液体ヘリウム」を作る時にも利用されています。

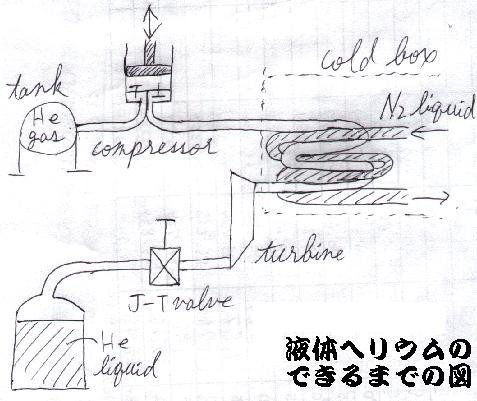
　まず、「ヘリウムガス」を圧縮した後、「液体窒素」にて冷却します。さらに「タービンで仕事をする」ことで「断熱膨張」させて「逆転温度以下」まで冷却し、最終的に「絞り膨張弁」で大気圧まで膨張させて、「ヘリウムの凝縮点」である"4.5K（-281.3℃）"の超低温を得るのです（下図）。

　では、

「なんで絞り膨張で温度が下がるのか？」

　その疑問に答えるには、「分子論的考察」が必要だったのです。

■「エンタルピー」のアナロジーとベルヌーイの先見性

　エンタルピーは何度も書くように、

H = U + PV

です。このうち

内部エネルギー"U"の「中身」

は、分子論的には

分子間の「相対的運動エネルギ」と分子間力による「位置エネルギ」

です。

　つまり改めて書くと、

「エンタルピー」=「分子の運動エネルギ」+「分子の位置エネルギ」+「圧力のエネルギ」

という事になりますが、これと酷似した式があります。

そうです、理想流体の定常流での「ベルヌーイの定理」

(1/2)ρv^2 + ρgh + P = const.

です。

　これは、一本の流線上における

単位体積当たりの力学的エネルギ保存則

を表わしていると言えます。

　つまり、流体においては

微視的にも巨視的にも「エンタルピー」という形でエネルギが保存

している事になります。ただし、「摩擦損失」等があると、

流線ではなく「管全体」を一つの系と見てエネルギが保存される

事になります。

　ベルヌーイはいち早く、流体を微粒子とみなして流体の運動を捉えていました。気体分子運動論も、彼が早くから提唱していました。

　彼の分子論につながる先見性は、まさに流体運動の本質を捉えていた事によるものです。しかし、世の中が受け入れるには、彼の理論は先に進み過ぎていたのです。

　先見性があり過ぎると、人々に受け入れられないのも世の常ですね。それは、本質的過ぎる概念というのは捉え難く、肉付けをして形あるものとして見せることで、やっと多くの人が理解できるようになるからです。