
マーケティングリサーチで使われるコレスポンデンス分析について調べてみた
お仕事でコレスポンデンス分析を使ったアウトプットを提出する機会ができました。せっかくのチャンスと考えて「コレスポンデンス分析」について以前から悩んでいた点も含めて色々と調べてみました。
※アイキャッチに深い意味はないです。
あくまで、このnoteはその結果をまとめたものです。参考文献は都度記載しますが学術的な正しさを求められても困りますので、その前提でお読みください。
コレスポンデンス分析とは?
リサーチの結果をクロス集計表で見る機会が多いのですが、表頭項目(列)と表側項目(行)が多いと内容を把握しにくい場合があります。
そこで項目間の関係性を視覚的に分かり易く表現するために、散布図を用いて見易くする手法がコレスポンデンス分析です。省略して「コレポン分析」と呼ばれることもあります。
要は「クロス集計表の結果をパッと見てわかる内容にした感じ」がコレポン分析の使い方です。
ちなみに「テキストマイニングによるマーケティング調査(上田、黒岩、戸谷、豊田)」によると、以下のような説明がなされています。
コレスポンデンス分析とは、名義変数や順序変数など質的な変数を集計したクロス集計表をもとにして、次元縮約を行う方法である。結果として、類似した項目(表側)同士の距離と、類似した変数(表頭)同士の距離を同時に算出することができる。これら得られた座標データからマップを作成することで視覚化されることが多い。
実際にやってみましょう。
以下の表は、あるスーパーにおいてN日間定点観測した結果、緑茶ペットボトルが購入された個数をまとめた結果です。年代別に見た時、年齢層と購入ブランドとの対応関係を考えてみましょう。もちろんだけどダミーデータですよっ。

ちなみに今回は分かりやすいよう5×5の表にしていますが、コレポン分析で使われるのは例えば20×20のような縦にも横にも長いクロス表だったりします。
全体的に見て「お〜いお茶」と「伊右衛門」が購入されやすいという傾向は見えますが、どの世代にはどの飲料が愛されているかはパッとは分かりませんよね。
そこで、コレスポンデンス分析を実行します。(実行環境はRです)
まずはデータの読み込み〜可視化(定番のモザイクプロット)です。
> drink <- read.csv("drink.csv",header=T,fileEncoding="utf-8")
> rownames(drink) <- c("生茶","伊右衛門","綾鷹","十六茶","お〜いお茶")
> mosaicplot(drink, main="drink") 
まずは、クロス集計表をグラフ化してみました。はっは〜ん、こうなってんのか、というところまでは分かります。
ちなみに、こんな見せ方もあります。
> library("gplots")
> dt <- as.table(as.matrix(drink))
> balloonplot(t(dt), main ="", xlab ="", ylab="", label = FALSE, show.margins = FALSE)
次に年齢とブランドの対応分析をするので、独立性の検定(カイ二乗検定)を行います。ここでは「年齢とブランドは関係無い(独立である)」という帰無仮説を立てます。「年齢とブランドは関係ある(独立でない)」が対立仮説になります。
> chisq.test(drink)
Pearson's Chi-squared test
data: drink
X-squared = 1064.8, df = 16, p-value < 2.2e-16P値が2.2e-16く0.05ですから、帰無仮説を棄却します。したがって対立仮説が選択され、年齢とブランドは独立でなく関連があると考えられます。
ここまで来て、このデータでコレスポンデンス分析をやっても大丈夫だよねと分かります。では、関数corresp( ) を使って分析を進めます。参考文献は同志社大学の金明哲先生の以下ページです。
> library(MASS)
> (drink.ca<-corresp(drink,nf=5))
First canonical correlation(s): 1.916009e-01 7.569667e-02 1.951804e-02 2.610063e-03 2.271203e-17
Row scores:(行の得点)
[,1] [,2] [,3] [,4] [,5]
生茶 -0.04101217 -2.8046510 1.88743322 -0.3807369 1
伊右衛門 1.05133536 0.4350201 0.04338852 -0.4761930 1
綾鷹 0.61999177 -1.0891432 -1.66637392 2.3219966 1
十六茶 -1.40647256 -0.7448768 -2.04486296 -1.8720021 1
お〜いお茶 -1.01132517 0.6388888 0.49765993 0.4961860 1
Column scores:(列の得点)
[,1] [,2] [,3] [,4] [,5]
20代 0.1403728 0.7084231 0.36989694 0.06579613 -1
30代 1.3514525 -0.6024383 -2.09543266 0.18493610 -1
40代 0.4611199 -2.0124736 1.22806285 -1.41805593 -1
50代 -1.5689402 -1.3044172 0.02268422 2.06585172 -1
60代 -3.1274862 0.4336237 -1.89086907 -2.56471438 -1金先生曰く「累積寄与率を計算するためには、nf=min(行数、列数)にしたほうがよい」とあるので、素直に従います。
各軸の寄与率を元に考察を行う必要がありますが、関数correspは寄与率を返さないようです。正準相関を用いて算出しなければいけません。
> ev<-drink.ca$cor^2
> round(100*ev/sum(ev),2)
[1] 85.72 13.38 0.89 0.02 0.00第2固有値までの累積寄与率は99.10%で、非常に高い結果となりました。したがって第1、2固有値に対応する得点のみを分析すれば良いでしょう。
あとはその結果を描きます。
> biplot(drink.ca,cex = 0.6)
年齢という観点で見ると、20代〜40代と、50代〜60代の2つのグループに別れそうな印象です。
ブランドという観点で見ると、生茶と、伊右衛門・綾鷹と、お〜いお茶・十六茶の3つのグループに別れそうな印象です。
ちなみに縦に計算して100%になるよう集計すると、確かに2つのグループに別れそうな感じがします。(色付けは横に行単位で実施しています)

横に計算して100%になるよう計算すると、確かに3つのグループに別れそうな印象です。(色付けは縦に列単位で実施しています)

MASSパッケージとは別に、caパッケージを利用しているコンテンツもよく見かけるので、こちらも実施してみます。
ちなみにcaパッケージ派とcorrespパッケージ派に分かれているようですが、なぜcaなのか・なぜcorrespなのかがわからずに苦戦しています。こちらどなたか教えていただけないでしょうか。
> library(ca)
> (drink.ca <- ca(drink, map="symmetric"))
Principal inertias (eigenvalues):
1 2 3 4
Value 0.036711 0.00573 0.000381 7e-06
Percentage 85.72% 13.38% 0.89% 0.02%
Rows:
生茶 伊右衛門 綾鷹 十六茶 お〜いお茶
Mass 0.079522 0.396324 0.093118 0.089136 0.341901
ChiDist 0.215621 0.204116 0.148334 0.278238 0.199955
Inertia 0.003697 0.016512 0.002049 0.006901 0.013670
Dim. 1 -0.041012 1.051335 0.619992 -1.406473 -1.011325
Dim. 2 -2.804651 0.435020 -1.089143 -0.744877 0.638889
Columns:
20代 30代 40代 50代 60代
Mass 0.601424 0.131330 0.113873 0.106030 0.047343
ChiDist 0.060425 0.266087 0.177766 0.316458 0.601299
Inertia 0.002196 0.009298 0.003598 0.010618 0.017117
Dim. 1 0.140373 1.351453 0.461120 -1.568940 -3.127486
Dim. 2 0.708423 -0.602438 -2.012474 -1.304417 0.433624
> plot(drink.ca, map="symmetric")

corresp関数とだいたい一緒の結果が返ってきましたね。
分析の見方に対する注意点
コレポン分析の結果を、どのように読み解けば良いでしょう。

30代~40代は「綾鷹」が好きで、50代~60代は「お~いお茶」「十六茶」が好き、でしょうか。
しかし、もう一度データを見て頂くと分かりますが、どの年代で見ても20代の購入量は圧倒的なのです。そのような見方は、数量で見れば違和感を覚えます。
それもそのはずで、コレスポンデンス分析は、それぞれ行得点・列得点を算出しているだけで、それらを重ね合わせたに過ぎません。
「ブランドポジショニングの理論と実践(豊田裕貴)」では、次のように述べられています。ここはめちゃくちゃ重要なので、少しだけ長くなりますが引用します。
次元縮約系の手法を活用したポジショニングマップは、ブランドを布置したマップと、評価項目を布置したマップの2つが得られることになる。主成分分析を考えればわかるが、これらのマップはそれぞれ異なる単位(片方は負荷量であり、片方は得点である)によって描かれたマップであることに留意しなければならない。もちろん、原点があるので、両マップを重ねることは可能であり、重ねて描かれたマップをバイプロットと呼ぶ。
バイプロットを用いるうえで気をつけなければならないのは、もともとが異なる単位で描かれているということである。通常、負荷量で描かれたマップは原点からの方向性で読み解くため、バイプロットの場合、負荷量の方を原点からの矢印で表記するという工夫がなされる。
問題は、コレスポンデンス分析の場合のバイプロットである。主成分分析や因子分析と異なり、コレスポンデンス分析の出力は、負荷量と得点という組み合わせではなく、行得点と列得点という得点同士の出力である。このことから、バイプロットを作った際、ブランドの位置と評価項目の位置を直接比較するという誤用が非常に多い。ソフトウェアによっては、得点の標準化を工夫することで、バイプロットでも行得点と列得点が比較しやすいように散らす工夫がなされることがあるが、標準化のいかんに関わらず、行得点と列得点の直接比較はできない。
※太文字は松本による
つまり列要素と行要素との距離は、数理的に定義されず「近い」「似ている」のように解釈できないのです。
日経リサーチにおけるコレスポンデンス分析のページでは以下のように注意書きをしてくれています。
ブランド・イメージの例でいえば、ブランド(行要素)間の距離は解釈できる。またイメージ(列要素)間の距離も解釈できる。しかし、あるブランドと、あるイメージ項目との、つまり列要素と行要素との距離は数理的に定義されず「近い」「似ている」のように解釈できない、という問題である。
ここで示した喫煙とブランドの2例においては、そのような解釈をしても違和感がないのだが、違和感がないにもかかわらず、実はそう見えるだけで、平面上の行要素と列要素の距離は実際には間違っている場合もある。
残念ながら、この問題は理論的には解決されておらず、解釈を間違える可能性もあるため、同時布置をすべきではないという立場もある(表示できないソフトウエアもある)。
現実には、同時布置図はマーケティング分野で頻繁に利用されている。イメージ項目で空間の方向性を解釈したうえで、ブランドに関する相対的なポジションを理解するというように分離して利用した方がよい。
※太文字は松本による
実際には、日経リサーチのコメントにある通りに実践した方が良いのでしょうが、私はもっと慎重派で、表側(行要素)と表頭(列要素)それぞれのバイプロットを作成して、2軸の解釈をした後に重ね合わせるのが良いのかもしれません。
「30代と綾鷹が近い。だから何かしら対応している」は、背景を知らないと言うだろうなと思いました。これは危うかった…。
主成分分析との違い
さて、ここまで来ると気になってしまうが主成分分析との違いです。コレスポンデンス分析と主成分分析、どちらも次元縮約系になるのなら、別に主成分分析でもよくないですか? と思ってしまいました。
まずは今回のデータで、主成分分析をやってみました。
> (pca = prcomp(drink, scale=T))
Standard deviations (1, .., p=5):
[1] 1.965418e+00 1.062797e+00 8.664976e-02 9.295267e-03 8.735626e-17
Rotation (n x k) = (5 x 5):
PC1 PC2 PC3 PC4 PC5
20代 0.5031966 -0.1368795 -0.3110184 0.2736259533 0.74595819
30代 0.4332951 -0.4916537 -0.4802308 0.0007908906 -0.58301781
40代 0.4799369 -0.3077034 0.6592130 -0.4849313031 0.07251915
50代 0.4552032 0.4192864 0.3589684 0.6260696469 -0.31010872
60代 0.3485673 0.6848782 -0.3304934 -0.5458998449 -0.04701237
> summary(pca)
Importance of components:
PC1 PC2 PC3 PC4 PC5
Standard deviation 1.9654 1.0628 0.08665 0.009295 8.736e-17
Proportion of Variance 0.7726 0.2259 0.00150 0.000020 0.000e+00
Cumulative Proportion 0.7726 0.9985 0.99998 1.000000 1.000e+00PC2まで見たら累積寄与率が0.99だったので、主成分2を観るまでで良さそうですね。ではplotします。
> biplot(pca)
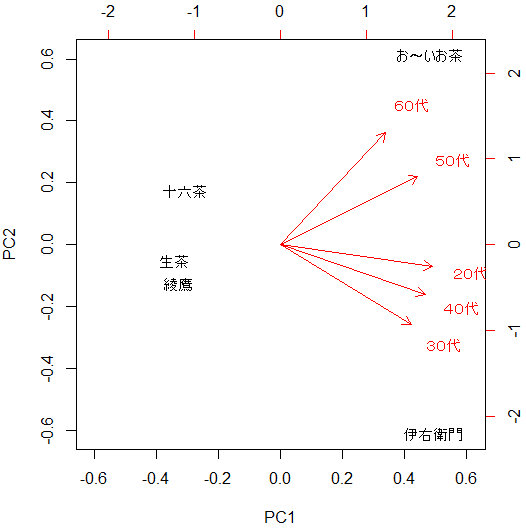
PC1が商品の売れ行き、PC2が好みの違いでしょうか。
コレスポンデンス分析と全く違うように見えますが、主成分分析のグラフを右に90度回転させて見比べると、主成分負荷量である年代と、列得点である年代は同じようにプロットされている…ようにも見えます。
じゃあ主成分分析でもいいの???
私の疑問について、既に流通科学大学(当時)の水本先生(現在は関西大学)がまとめておられました。ありがたや…先行研究大事…。
水元先生は論文の中で、次のようにまとめられています。
データ中の変数やケース間の差異を発見することが目的ではなく,できるだけ元の情報を圧縮したものを作り上げることにあるならば主成分分析がすぐれており,差異(類似)を見つけ出すことが目的なのであれば,コレスポンデンス分析が適していると考えられる。
目的が差異の発見ではなく,データを圧縮して関係性を見る場合には主成分分析,類似関係や差異を見つけることが目的であるならコレスポンデンス分析というように,一般的には分類できる。
①次元を縮約してPC1を最も説明力が高くなる総合指標とする主成分分析
②単なる行列項目の正準相関が最大になるように並べ替えてるだけなので主成分分析で言うところのPC1という概念が無いコレスポンデンス分析
こういう位置付けになるでしょうか。
列を縮約して新たな変数を生み出す主成分分析と、行列を並べ替えて「それっぽい関係性」を見つけ出すコレスポンデンス分析の違いとも言えますか。
主成分分析を実施して、PC2とPC3の結果と、コレスポンデンス分析の結果が一致するみたいな発見も書かれていましたが何か本末転倒感は否めませんよね。
今回のまとめ
自分が疑問に思ったことは、既に誰かが過去に調べている。(主成分分析と何が違うの?とずーっと思っていた)
コレスポンデンス分析は行・列をごっちゃにして分析しない。
いいなと思ったら応援しよう!

