
花びら5枚の花はなぜ多い
※ 1万字あります。難度は高めです。
∫1 はじめに
花びらが5枚または5裂の花が多い気がしませんか?
偶然というには無理があるほど、5に偏っています。
花びらが5枚/5裂になりやすい要因があるかもしれません。

分類学はさておいて、ぱっと見で5が多い。
自然界には白花が多いので、「5」かつ「白」の花はたくさんある。

∫2 花のつくりを理解する
要因の検討に入る前に、花のつくりを理解する必要があります。
■1 数性とは
花を構成する部品が、特定の数で整えられているように見えるとき、
専門用語で「数性がある」といいます。
5が目立つときは「5数性」といいます。

目に留まりやすい要素として、以下の部位があります。
① 雌しべ: 子房の形、柱頭(雌しべの先っぽ)の裂数
② 雄しべ: 本数
③ 花びら: 枚数または裂数
④ ガク : 枚数または裂数
最も派手なのは花びらなので、花びらが5枚の花が咲いていると、
「5が目立つなあ」ということになります。
1)花の外周を構成する、一連のグループがある
花びらと関連が強いのは、内側にある雄しべと、外側を支えるガクです。
[ 雄しべ ] - [ 花びら ] - [ ガク ]
この3部位は、分化発生学的に近い、一連のグループと考えてください。
[ 雄しべ は 花びら化することがある ]

雄しべが花弁化すると、八重咲きになる。
ハイビスカスの雄しべが花弁化すると、先っぽ部分がフサフサに。

花びらに なってみようか やめようか
[ガクが花びらっぽくなることがある ]

ガクが花びら化し、5枚+5枚=計10枚の花弁に見える。
防御や支えがない状態は容認できないらしく、外周を3枚の苞で守っている。
右:チューリップ(ユリ科)3数性
ガクが花びら化し、3枚+3枚=計6枚の花弁に見える。
つぼみの時点では、ガクは緑色で厚みがあり、防御力も高そうにみえる。

花びらとガクが合着したような筒が、しべを包んでいる。
どっちつかずで説明に困るタイプを、学者は花被と呼ぶことにした。
最外層にあるボート状の構造物は苞。
2)グループ間の数性は、異なっていてもよいことにする
・[ 雄しべ ] - [ 花びら ] - [ ガク ] グループの数性と、
・[ 雌しべ ] - [ 子房 ] グループの数性と、
・[ 葉 ] - [ 苞 ] グループの数性が、
一致するとは限りません。
グループ間の数性は、異なっていてもよいことにします。

3枚の苞で、3個の花を包む。
5本の雄しべ、5稜の花冠、ガクは筒状。
3)倍数が出やすい
ときどき、倍数が出現します。
倍数が出現したときは、小さいほうの数を採用します。
細胞は二分裂するものなので、倍数は出やすいでしょう。

雄しべ5本 左上:ミツバツツジ 右上:レンゲツツジ
雌しべ10本 左下:シャクナゲ 右下:セイシカ
4)数性は目につく「傾向」にすぎない
現存する花の形は、さまざまです。
実際には、以下のケースもたくさんあります。
・数性を決めるのに使う、花びらやガクがない
・数が多すぎて、数性を考えられない
・2種の数を採用している
・最頻値があるだけで、数が絞り込まれていない
・数性が科の中の属でばらばらで、系統的特徴ではない
[ 花びらやガクは、必ずあるとは限らない ]

左中:サトイモ科 右中:クワ科 集合花
左下:ドクダミ科 右下:ヤマモガシ科 集合花。飾りは苞が担う。
[ 数が多すぎて、いくつ?と聞かれても困る ]

右上:ハス科 雄しべ多数、花弁多数。ガクと花びらの分化は微妙。
左下:サボテン科 雄しべ多数、花弁多数。ガクと花びらの分化は微妙。
右下:ハマミズナ科 雄しべ多数、花弁多数。ガク5。雄しべと花びらの分化は微妙。
[ 数えられるけど、決めかねる ]

左:雌花 花弁3枚+ガク2枚=計5枚に見える。
右:雄花 花弁2枚+ガク2枚=計4枚に見える。
雌雄で形の特化が進んでいる花では、数を統一して考えることが難しい。

左:雌花 花被4、ときどき3。
右:雄花 花被3、ときどき4。
雌雄で偏りが異なる。

雄しべは5~7本で不定。ガクと花びらは分化が微妙で、数は不定。
花弁と雄しべの配置に規則性がなく、数で構造を決め打ちする傾向が弱い。
雌しべ先熟型。中央は雌性期、右は雄性期。
全体として数性は、あったりなかったり、強かったり弱かったりです。
数性は、生物を強力に支配する「法則」ではなく、
①目を引くことの多い、②傾向 と考えてください。
■2 「放射対称」と「左右対称」
花の形には「放射対称」タイプと「左右対称」タイプがあります。
・放射対称タイプ: 上向きの花に多く見られます。
・左右対称タイプ: 横向きの花に多く見られます。
左右対称タイプにも数性は出現するのですが、
雄しべが痕跡化したり、花弁が変形したりしていて、数えにくいです。
本記事では、変形の程度がひどくない、放射対称寄りの花を考えます。
[ 左右対称の花] 上下を考慮して花の形を整えている

スミレ程度の変形であれば、写真を使って数えられる。
シソ科とマメ科は難しい。
[ 放射対称/左右対称は、科の中でばらばらのこともある ]

左:ゲラニウム(放射対称) 右:ペラルゴニウム(左右対称)
変形がひどくないので、問題なく部位の数を数えられる。

左:ムラサキツユクサ(放射対称) 右:ツユクサ(左右対称)
左右対称が進んでも、花弁3枚、雄しべ6本で、数性を維持している。
∫3 数性の分布
数性の全体像を把握します。
以下の科をピックアップします。
① 数えやすい
② 数が決め打ちで、揺らぎにくい
③ 科を見渡したとき、特定の数に数性が集中している
花びらの数が安定していれば、それだけで「数性あり」にします。
雄しべの本数を増やし、フサフサにするのは、よくある戦略です。
逸脱を許容します。
バラ科のワレモコウは横咲きで、花弁欠損、雄しべ4本、ガク4裂ですが、
バラ科全体に5弁の性質が頻出しますので、5を採用します。
[ 調査結果 ]
3数性:アヤメ科、ユリ科、ヒガンバナ科、キンバイザサ科、ツユクサ科、
パイナップル科、キジカクシ科、シュロソウ科、ミズアオイ科、
ラン科、アケビ科、ヤマノイモ科、クスノキ科、ウマノスズクサ科
(雄しべ多数)オモダカ科、バンレイシ科
4数性:アブラナ科、アカバナ科、カキノキ科、ジンチョウゲ科、グミ科、
ミズキ科、マンサク科、キブシ科、ジュズサンゴ科、モチノキ科、
(雄しべ多数)ケシ科
5数性:キク科、アジサイ科、サクラソウ科、フウロウソウ科、アマ科、
キョウチクトウ科、リンドウ科、ツツジ科、ナス科、トベラ科、
イソマツ科、ツツジ科、ナデシコ科、カタバミ科、センダン科、
ハゼラン科、オシロイバナ科、ハナシノブ科、ベンケイソウ科、
キキョウ科、ムラサキ科、セリ科、ヒルガオ科、スイカズラ科、
クロウメモドキ科、ノボタン科、イワタバコ科、トケイソウ科、
ガマズミ科、エゴノキ科、パパイヤ科、スミレ科、ウコギ科、
キントラノオ科、(雄しべ多数)バラ科、アオイ科、オクナ科、
キンポウゲ科、フトモモ科、スベリヒユ科、オトギリソウ科、
マタタビ科、ホルトノキ科
6数性:ミソハギ科、
クチナシ(アカネ科)、アカバナチシャノキ(ムラサキ科)
7数性:ツマトリソウ(サクラソウ科)
8数性:チョウノスケソウ(バラ科)
全体傾向は、以下のようになりました。
● 一番多いのは、5数性。
● 平行脈が、3数性に集中している。
● 網状脈では、多い順に、5数性、4数性、3数性。
● 6、7、8数性は稀。
[ 一番多いのは、5数性 ]

上段 : バラ科、ツツジ科、キョウチクトウ科、アオイ科
下段 : サクラソウ科、ナデシコ科、キンポウゲ科、カタバミ科

筒状花は、雄しべ5本、花冠5裂。
飾ることに特化している舌状花は別に考える。
キク科は巨大グループで、科一つでヒストグラムを引っ張るほど。

アジサイ科のウツギ属は、種によって4、5、6が最頻で出る。属全体では5の種が多い。
アジサイの両性花は、通例、雄しべ10本、花びら5枚で、株内で数に揺らぎがでる。
[ 平行脈が3数性に集中している ]

上段 平行脈 : アヤメ科、ユリ科、パイナップル科、ラン科
下段 網状脈 : アケビ科、バンレイシ科、クスノキ科、ウマノスズクサ科

左: スズラン属(キジカクシ科)
中: ミラ属(キジカクシ科)
右: イスメネ属(ヒガンバナ科)

葉脈の平行性は、スジのきついものから分岐や曲線を含むものまで、グラディエーション。
ドラセナはゆるめの平行脈。中心の左右で筋の方向を変えており、中央部の幅が広い。

ユリ目では例外的に網状脈。本種は3へのこだわりが顕著。
[ 網状脈には、4数性も出現する ]

上段: ミズキ科、ジンチョウゲ科、グミ科、マンサク科
下段: アブラナ科、アカバナ科、ケシ科、ジュズサンゴ科
上記のうち、ミズキ以外は子房上位。
[6数性は稀 ]

左:サルスベリ ほぼ6数性で安定。花弁とガク裂は互生で、数は一致。
中:ミソハギ ほぼ6だが5も出る。花弁とガク裂は互生で、数は一致。
右:ザクロ 6±2で揺らぐ。6は数性というより最頻相当。花弁とガク裂はほぼ互生。

アカネ科は属によって数性が異なる。
クチナシ連は、種によって数が5~10と数性の幅が大きい。
種の数性にかかわらず、雄しべと弁裂は互生を保ち、数が一致する。

ムラサキ科の基本数は5。たまに6になった花が見つかる程度。
ただし、コーディア属は、最頻5の種と最頻6の種を抱える。
数性にかかわらず、雄しべと弁裂は数が一致する。
部品の数を数えるだけでは、数性を明言できない科が複数あります。
・数に不定性がある
ウリ科:花びらは5裂安定。雌雄異花で雄しべは3~5本で不定。
タデ科:花冠はほぼ5裂。雄しべは5本+増量分で不定。
ツバキ科:属によって5が出るが、科全体として不定。雄しべ多数。
モクレン科:属によって3が出るが、科全体として不定。雄しべ多数。
・数に不一致がある
オミナエシ科(マツムシソウ目):雄しべ4本、花冠5裂。
マツムシソウ科(マツムシソウ目):雄しべ4本、花冠5裂。
ノウゼンハレン科(アブラナ目):雄しべ8本、花弁5枚。
アブラナ科(アブラナ目):雄しべ6本、花弁4枚。
・シソ目
キリ科:雄しべ4、花冠5裂。左右対称。
クマツヅラ科:雄しべ4。花冠は5裂。
ノウゼンカズラ科:雄しべ4、花冠5裂。左右対称。
シソ科:雄しべ2本か4本。左右対称。
キツネノマゴ科:雄しべ2本か4本。左右対称。
オオバコ科:雄しべ2本か4本。左右対称。
ゴマノハグサ科:雄しべ2本か4本。左右対称。
モクセイ科:雄しべ2本。花冠の裂数は4、5、6~多数。
・属によって数性が異なる
メギ科:属によって3、4。雄しべ一致。
ブドウ科:属によって4、5。雄しべ一致。
アカネ科:属によって4、5、6、それ以上。雄しべ一致。
ニシキギ科:属によって4、5。雄しべ一致。
ユキノシタ科:属によって4、5。雄しべ一致。
ミカン科:属によって3、4、5裂。雄しべ多数。
・その他
ショウガ科:たぶん3数性。変形が進んでいて、数を確認しかねる。
マメ科:たぶん5数性。変形が進んでいて、数を確認しかねる。

祖先は雄しべ5本で、進化の途中で本数を減らしたらしい。
左:ベロニカ属(オオバコ科) 雄しべ2本、花冠4裂、ガク4裂
中:ルリハナガサ(キツネノマゴ科) 雄しべ2本、花冠5裂
右:ジャスミン属(モクセイ科) 雄しべ2本、花冠の裂数はさまざま

左:イクソラ 4数性
4数性は他に、ヒナソウ、ヤエムグラ、ナガバハリフタバムグラなど。
中:コーヒー 5数性
5数性は他に、コンロンカ、ヘクソカズラ、ペンタス、ハクチョウゲなど。
右:ティアレタヒチ 8数性
下位分類のクチナシ連はさまざまな裂数を含むグループ。
細かく言えばいろいろありますが、
全体的には当初の印象の通り、「5が多め」で合っています。
全体傾向(再掲)
● 一番多いのは、5数性。
● 平行脈が3数性に集中している。
● 網状脈は多い順に、5数性、4数性、3数性。
● 6、7、8数性は稀。
∫4 数性の考察
本題です。
■1 花芽を作ろう
立体を隙間なく充填できる形に、6角で構成された形があります。
ハチの巣に規則的な6角形が見られるのは有名です。
(専門用語で六方最密充填といいます。本記事では6角充填と呼びます)
本当は細胞は球状の形をとりたいのですが、周囲にも細胞がいます。
丸い細胞同士で「押しくら饅頭」をすると、6角充填で落ち着きます。
細胞でカドができる、基本の仕組みは、丸型 ⇒ 6角です。
ハチの幼虫が過ごす部屋の場合、球に近い形でないと不都合ですが、
植物の細胞では、長辺、短辺の差が大きい長6角形でも問題ありません。
細胞の形は融通が利きます。
授業で観察した玉ネギの細胞の形は歪んでいたでしょう。
採取した部位によって、4角に近かったり、6角に近かったりします。
平行線が決め打ちされているときは、4角充填も落ち着く形の一つです。
さて、花芽を作りましょう。
花を突きだして、虫に止まってもらいたい。
先端を尖らせた、尖塔型のツボミを目指します。
土台の工事が始まります。
このとき、6角充填から外れる必要が生じます。
6角充填は平面が決まっているときに向く形で、尖塔用ではないです。
「上に向けて尖らせるぞー」と押し合って、
サッカーボール配置になって、落ち着くかもしれません。
中央に5角形の細胞1個、6角形の細胞を周囲に5個。
これで中央が尖った形になる。
5辺を土台にして、花弁や雄しべになる細胞を積んでいけば、
都合よく花芽の工事が進みそうです。

■2 クォーターロゼット咲きのバラ
突然ですが、バラの咲き方にクォーターロゼットというのがあります。
クォーターは、四分の一の意です。
中央部がおおむね4つに分かれた状態で、花弁がぎっしり詰まります。
「花びらの原基をねじこむスペースはもうないのに、
もっと花弁を増やせと指令が来るんだ。しかも渦巻き禁止だって。
現場のことも考えてよ。ごめん、もう無理、1つ落ちて!」
バラは5数性で、土台は5のはずです。
場所がなさすぎて、数がひとつ落ちたように見えます。

ごちゃごちゃしていてわかりにくい。花びらみちみちなのだけはわかる。
4分割のほか、3分割が出ることもある。

■3 3数性の花
アヤメ、ユリなど、平行脈の植物は、3数性に集中しています。
平行脈で安定性の高い形は4角充填です。
もともと4角充填していたところ、尖塔作りでひとつ減ったとか?
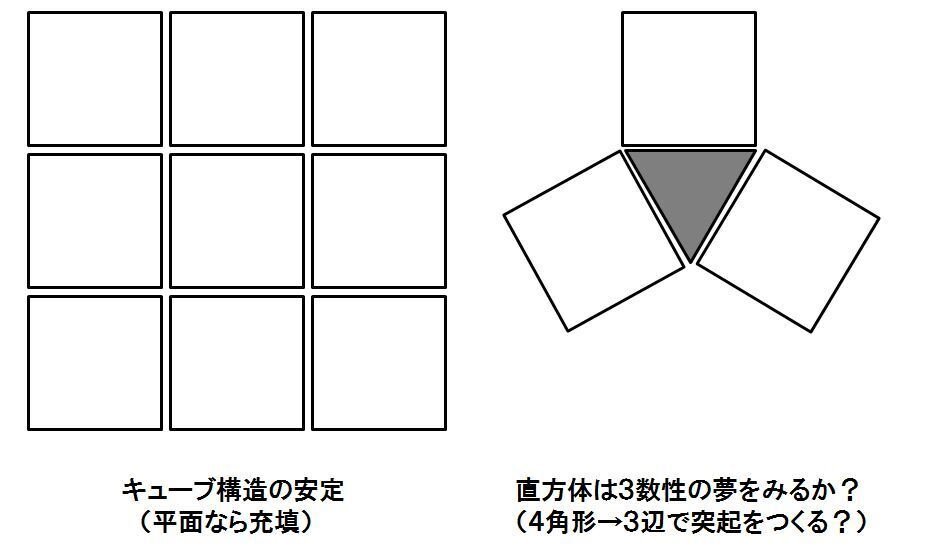
■4 椅子取りゲームモデル
6角充填だったものが、尖塔作りで5に減る(6 ⇒5)
5辺だったものが、場所を確保できなくて4に減る(5 ⇒4)
4角充填だったものが、尖塔作りで3に減る(4 ⇒3)
一つずつ数が減るのが特徴なので、
「椅子取りゲームモデル」と仮称します(瀬戸による呼称)。
6 ⇒5でなく、6 ⇒4になるケースはありうるでしょう。
椅子取りゲームで、一度に二脚、抜くようなものです。
■ 5 幾何学で考えすぎないように
サッカーボール構造の安定は、数学者が好みそうです。
生物に幾何学が出現すると、その美しさに魅了されますが、
生物の現象に幾何学を「適用」しないほうがよいです。
細胞は、変形を容認するユニットであって、固い板ではないです。
カドはなくせますし、カドを増やすこともできます。
縦に引き伸ばしたり、横に潰したりもできます。
柔らかい細胞が融通しあって、結果として幾何学図形が出現することと、
カドのある硬い板を用意して、模型を組み立てることを同義にはできない。
自然現象には、因果の方向があります。
科学における考察では、因果の方向に慎重でなくてはなりません。
等号の左右を区別しない数学とは異なります。
■ 6 生物を制限する「資源」と「余地」
生物は「資源」と「余地」という物理要因の影響を受けます。
「資源」がクリティカルであることは、理解しやすいでしょう。
植物は、光や肥料が不足すると生育不良になります。
動物は、食糧がなければ餓死、ビタミンがなければ欠乏症になります。
もう一つ。
生物が存在するためには、「余地」が必要です。
コンクリートの隙間で頑張る植物はド根性植物として愛されます。
狭いといっても多少の余地はあるので、なんとか生きていけるようです。
組織や細胞には容積がある。
この容積をなかったことにはできない。
資源ほどクリティカルではないにせよ、余地も制限要因になります。
鳥のヒナが成長したければ、殻を割って出るしかありません。
卵や胎児が大きいと、産道を通過しにくく、難産になりやすいです。
ヘルニアになると、狭い場所で神経が圧迫されて痛みます。
親不知は、歯が生える場所がないので空いている場所に出ようとします。
通常、スイカは球形ですが、型にはめると四角いスイカができます。
余地がなければ分裂を断念し、余地があるところではよく分裂します。
残念ながら、救出は絶望です… pic.twitter.com/Sfqesq2DhN
— yoto2nd (@yoto2nd) August 7, 2024
発生学では、細胞サイズで経過を考えます。
細胞容積一つ分のスペースを確保できないときは、
カタチを変形してもらったり、
密集地域からズレて下がってもらったり、
分裂して二つになるのを断念してもらったり、
存在するのを諦めて(自殺して)もらったり、
する必要があります。
このことが、将来の形や構造の起点になることがあります。
発生の一番最初のところに、卵割があります。
この工程では、サイズと位置を考慮した、かなり精密な配置がなされます。
細胞には、容積がある。
脂質二重膜には、厚みがある。
線維には、太さがある。
現実は、物理、すなわち、物「体」が意味を持つ世界です。
数学で、点に大きさがなく、線に幅がないのとは、違います。
■7 押しくらまんじゅうをもっと細かく
花芽ができる、最初のところはよくわかっていません。
もしかすると、押しくらまんじゅうは、等質ではないかもしれません。
たとえば、「花芽を作れ」というホルモンの指令を感知した、
最初の一つの細胞が切り込み隊長になるケースです。
切り込み隊長が突起になって、活路を開きます。
周囲の兵隊たちは「隊長のあとに続けー」です。
ただし、突破孔が狭いので、脱落者が出るのを避けられない。
隊長が猛進しすぎて、脱落者2名になることもあるかもしれません。
隊長が先走りすると、子房上位になりそうです。
(4数性は、子房上位の比率が高い)
隊長の重役出勤もあるかもしれません。
隊長「まずは準備に専念します、分裂への参戦はあとにします」
周囲の細胞たちは、陣形の誘導なしで、各自、自由にします。
仮に「隊長はあとから」が起きた場合、子房下位になりそうです。
(ミソハギ科やアカネ科は子房下位です)

「総帥から分裂命令が出てる。待てない」
「陣形はどうします?」「知らん」
「オレはやるぜ」「オレも分裂するぜ」
「狭いよ、どけよ」「そっちこそどけって」
「上の圧がゆるい、天井を押すしか。隊長はまだか」
「椅子取りゲームモデル」も、「子房位置モデル」も
調べてみないと本当のところはわかりません。
データなしで、想像だけでモデルを立てると、たぶん派手に転びます。
∫5 余談 動物で余地問題
若かりし日、僕は、代謝内科の研究室に転属しました。
新しい分野に着手するときは、最初に基礎知識を取得します。
まずは、総説(論文のまとめサイトに相当)をたくさん読みました。
次いで、時間の許す限り、学会の教育講演を聞いて回りました。
当時、生活習慣病分野は、生化学が花盛りでした。
肥満細胞は脂質の貯蔵庫というだけでなく、分泌細胞でもあります。
肥満細胞が肥大するとアディポネクチンの分泌が低下し、
さまざまな問題が起きる・・・。
生化学病因論が活況の中で、毛色の違う講演が混じっていました。
その講演者は組織学が専門でした。
肥満細胞が肥大すると、隙間を通る毛細血管が圧迫される。
肥満細胞は、自身の肥大が原因で、血流不良の環境に置かれる。
アディポネクチンの分泌低下に、血流不良が関わっているかもしれない。
映し出された肥満細胞は、脂肪滴でパンパンに膨れ上がっていました。
隙間に極細の血管が通っていますが、血球は通りにくそうです。
動物の細胞は細胞壁がないので、植物に比べて柔軟です。
通常は変形で圧を吸収します。
それでも余地の要素が、病理と関わる可能性はある。
脳内が生化学と遺伝学でいっぱいになっている僕に、
「物理要因もあるかもしれない」の講演は驚きでした。
∫6 終わりに
星型は図形として、めちゃくちゃカッコよいです。
「よくできました」のマークには、サクラの5弁花が使われます。
チューリップやヒマワリではなく、サクラです。
恒星は、5角の星型で描きます。
恒星は星型ではないのにです。
光の放射なら4角や6角でも表現できそうですが、なぜか5で描きます。
5角の星型はカッコよすぎて、必要以上に執着してしまいそうです。

サボテン全体でみれば稜の数は8~20が多く、5稜は決してメジャーではない。
本種は星形に観賞価値があり、サボテン愛好家に人気がある。
アストロという学名もナイス。
画像提供:AKuptsovaさん
生物は「たまたま」を系統的に引きずることがあります。
重篤な問題がないのであれば、最初に選んだ形を踏襲するのはアリです。
大きく4つの可能性があるでしょう。
① 構造理由:花芽を作るには、こうするしか道がない
(ボトムアップ、シーズ、生産現場の都合)
② 選抜理由:完成品の合目的性がクリティカルで、淘汰で絞り込まれた
(トップダウン、ニーズ、市場における売れ筋の都合)
③ 従前理由:当時のことはわからないが、前任者はそうしていた
(開発の手間をかけたくない、または、伝統縛り)
④ 理由希薄:①②③の背景がどれもなかったので、適当に決めた
三番目の「従前」は、手間要らずで無難です。
構造を変えたければ、遺伝子が変異するのを待たなくてはなりません。
新製品を上市したとして、想定外の問題を含んでいるリスクもあります。
長い目でみれば、
・政権交代: 有能な革新派が、保守派を破って議席を占める
・大災害: 新しい環境条件が、絶滅寸前まで淘汰のナタを振るう
は起きるのですが、メインで使われる方針は従前です。
遺伝は、先代と同じ形質で次代を構築する仕組み、すなわち従前です。
四番目の「理由希薄」の可能性は、有力な仮説があっても除外されません。
文字には、表音文字系統と、表意文字系統があります。
たぶん、文字の開発をスタートしたときの、着眼のたまたまです。
霊長類の中で、ヒトだけがアスコルビン酸を合成できません。
たぶん、始祖が欠損変異を持つ家系だったという、たまたまです。
アミノ酸にはD体とL体があります。
生物はL体を使うことに決めましたが、これもたまたまかもしれません。
「神はサイコロを振らない」どころか、
縛る要因がないか、縛りが弱ければ、いつでもサイコロを振るでしょう。

キンポウゲ科の基本数は5。花弁がある属はガクも5で、配置は互生で固定されている。
クレマチス属はその花弁を欠く。花弁のように見えるのはガク。4,6,8がいいらしい。
シュウメイギクやニリンソウを含むアネモネ属も、花弁のように見えるのはガクで、数が乱れる。
従前の要因に縛られないのは、始祖だけとして、
タイムマシンで当時の「1回、出たら目」を観察することはできません。
「花びら5枚の花はなぜ多い」という命題を立てたことについて、
自然は「たまたまっぽいけど気になる? ヒトは5が好きなんだね」
と笑って見ていそうな気がします。
長い記事も終わりになりました。
花びら5枚の花も。そうでない花も。
どちらもかわいがっていただけたら幸いです。
(瀬戸 裕紀)
掲載写真はスイカとアストロフィツムを除き、全て著者による撮影です。
本記事の著作権は瀬戸裕紀にあります。
以下の出典表示が可能です。
「花びら5枚の花はなぜ多い」, 瀬戸裕紀. SNSnote, 2024年8月3日
https://note.com/julikis_seto/n/nef48578191eb

