
まなびテクシリーズ 受験数学編
以前に『解法の壁』という記事を書きました。
ここでは、もう少し具体的に、数学の勉強方法、特に応用力をつけるための方法を紹介します。
まずは、高校生って本当に忙しいですよね。
進学校であれば、毎日課題がだされ、英単語もほぼ毎日覚えなければいけない。
週末課題もある。
人のネットワークを広げるために好きでもない部活もする。
本当に大変だ。
こうした時間がない状況に立たされると、どうしても人は『早く終わらせたい』という考えになる。
気持ちはものすごくわかる。
しかし、特に思考力を必要とする数学において、『早く終わらせよう』という考えが先行すると、
パターン①:わからないとすぐに解答をみて理解し、解答をそのまま写す
パターン②:わからないとそのまま解答を写す
パターン③:人に聞く
パターン②は最悪だが、大変の時間がない高校生はパターン①で勉強している。
ここで問題になるのは、『失敗せずにゴールまでたどり着いている』という点である。
わかりやすく言うと、
『迷路の地図を見ながら迷路を移動している』
では、なぜ数学においてこの方法が全く意味をなさないか。
以下の図を使いながら説明します。
数学の問題のスタートからゴール(正解)を目指す。
数学の解法はさまざまな正解がある。
そして、これ以上次の立式・計算に進めない壁も存在する。
それを以下のようにあらわす。

①個別指導・集団指導・質問対応などでゴールを目指す場合
最初から間違えを教える講師はいないので、最短距離の解法だけを教えてくれる。最速でゴールにたどり着けるだろう。

すると、この問題にはこれ以上は立式・計算できない壁があることを認知できずに、次の単元に進めてしまうことになる。

②参考書で自習学習でゴールを目指すルート
最初は自分で考えるので、多少回り道をしてしまうが、解答を見ることで、そこからは最短距離でゴールにたどり着くことができるだろう。

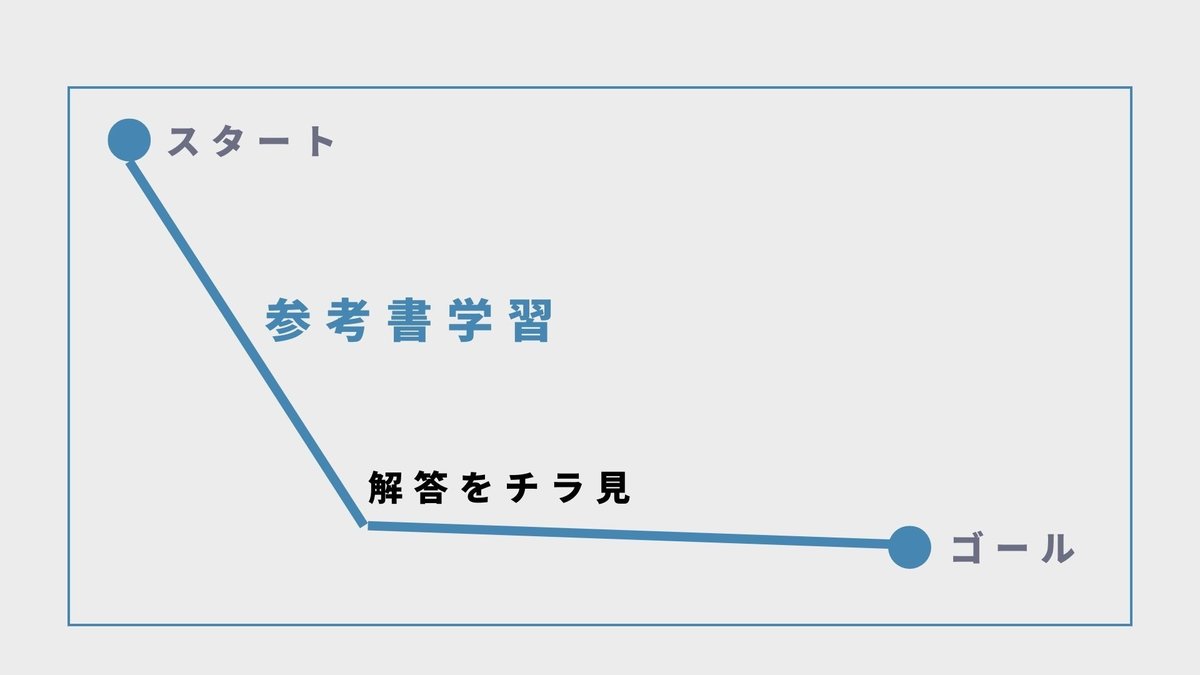
結果的に、この場合も、この問題にはこれ以上は立式・計算できない壁があることを認知できずに、次の単元に進めてしまうことになる。

③何度失敗してもゴールを目指すルート
この方法はたくさん失敗してゴールを果たすので、結果的に時間はかかりますが、必ず共通テストや特に国公立2次試験では効果を発揮します。
問題の『行ってはいけないルート』も知ると、類似問題が出題されても、『迷路』を上から見た状態つまりは『迷路』の地図をすべて知った状態で問題に取り組むことができるので、試験本番では、最短ルートでゴールにたどりつくことができるという仕組みなんです。
問題の『行ってはいけないルート』知らないと、『迷路』を『迷路』として通常通り進まなければいけないため、試験本番では解くのに時間がかかってしまうんです。

たとえば、友達と初めての目的地までドライブに行く際に、ちゃんと事前に混み具合や道路の大きさをGoogleマップ・ストリートビューで調べておけば、当日最短時間で目的地までたどり着けるということです。
だから、効率がよいと思われる『人に聞く』『解答を見る』という勉強法は『受験』においては一番結果が残せない方法で、実は一番効率が悪い学習方法なんですよね。
逆に『自力』で何度もゴールに立ち向かう勉強法は効率が悪いようですが、『受験』においては最大効率化できる学習方法であるということを高校生、受験生には知ってほしい。
