
『双子の幼女とチェス盤の部屋』解答
昨日の問題の解答です
この問題は数学問題なのですが
ぼくは算数きらいなんで
なんとか極限まで文章で説明してみました
まず作戦の基礎として思い付くのは
『8×8のチェス盤に1~64の数字をふる』
という事でしょう
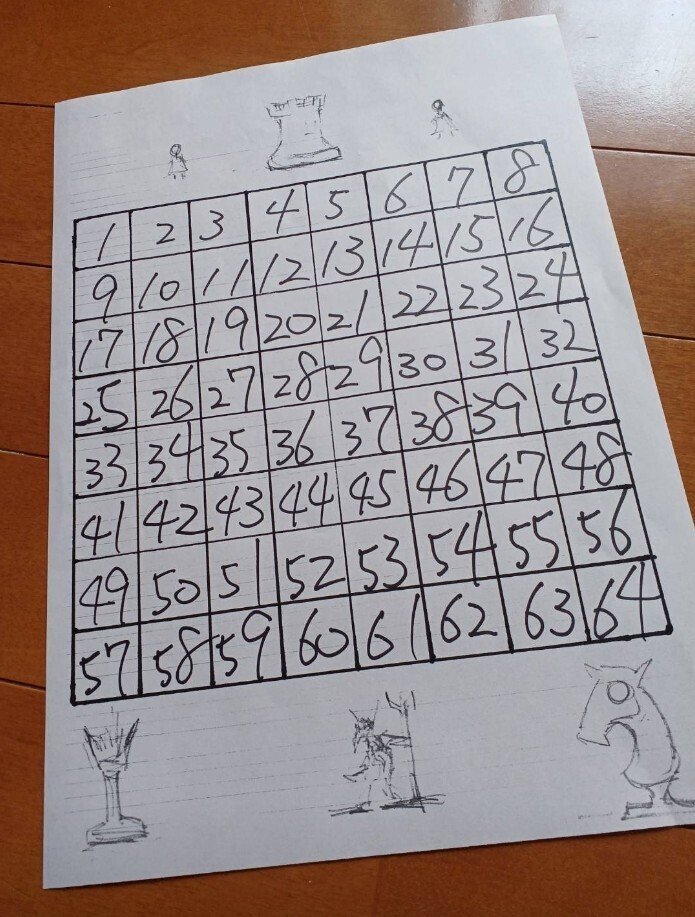
考え方としては勿論それでOKですが
それはいったん置いておきます
少しずつ問題を整理していきましょう
全てのマスはそれぞれ
ポーンがあるかないかという
二通りの状況下にあります
これ、チェスの駒でなく
オセロやコインの裏表で考えた方が
イメージしやすいかもしれません
僕はオンとオフのスイッチが
ずらっと並んでるイメージでとらえました

幼女Aの作業は
『スイッチを一ヶ所だけ切り替える作業』
だと思ってください
まったく途方にくれますよね
たった一ヶ所のスイッチを切り替えるだけで
1~64のどの数字かを言い当てるなんて
不可能に思えます
けれども少しだけ肩の荷を下ろしましょう
幼女Bに要求されているのは
『1~64のどの数字かを言い当てる事』だけで
盤面の再現等はなにも求められていません
つまり数字さえ当てればよいのです
すなわち盤面の情報を圧縮し
必要な情報だけを伝えるために
捨てるべき情報は捨てる事が肝心です
ではまず最初に
解き方の方向性の確認として
2マスだけの盤面を想像してみます
悪魔が告げる数字は1か2のどちらかとします
ポーン有を○、ポーン無を✕とすると
考えられる盤面は
○○、○✕、✕○、✕✕
この4通りです
そして幼女たちは事前に『悪魔が告げる数が1なら左のマスを○にし、2なら✕にする』という作戦を共有しておきます
そうすると幼女Aの指すべき手は
正解が1の時、盤面が
○○なら→右のマスのポーンを取る
○✕なら→右のマスにポーンを置く
✕○なら→左のマスにポーンを置く
✕✕なら→左のマスにポーンを置く
正解が2の時、盤面が
○○なら→左のマスのポーンを取る
○✕なら→左のマスのポーンを取る
✕○なら→右のマスのポーンを取る
✕✕なら→右のマスにポーンを置く
となります
どうでしょうか
4通りの盤面×告げられる1or2の数字を
ポーンひとつの操作でなんとか捕まえました
『伝えたい情報が既に盤上にあるのに幼女Aは盤面に手を加えねばならない』という命題もなんとかクリアー出来ています
『幼女Aの指し手の逃がし場所がある』
とでも言いましょうか
方向性としてはこれで合っていますが
これを8×8の盤面でやるには
さらに情報の精度を上げる必要があります
『ポーンをひとつ動かす』という動作の中に
どうにかして
可能な限りありったけの情報量を
詰め込んでやる必要がありそうです
ここらで閃きが必要になってきます
前述した盤面の性質
オンとオフの二面性
そしてこの問題が
数学の問題であるという事実を踏まえると
そういえば数字の世界にそういう
『イエスorノーの二択みたいな概念』が
そういうのがあったなと気付けるかどうか
そして知っているかどうかになってきます
(ちなみに知らないならゼロから自分で発明する必要があり『ゼロ知識でもド天才ならあるいは可能』と前述したのはここらの事です)
はい
それはなにかといいますと
『二進法』と『奇数・偶数』です
奇数と偶数については割愛しますが
ここで二進法については説明しときます
二進法はコンピュータなどで使われる
0か1かで数字を表記する方法です
普段われわれは
1~10までの十進法で生活してますが
それを0か1かで表記するのが二進法です
十で繰り上がるのでなく
倍々で繰り上がっていきます
1、2、4、8、16、32、64、、という感じで
倍々で数の桁が上がっていき
それぞれの桁が『有るか無いか』
つまり『0か1か』だけで表記する感じです
例えば44という数字は
32と8と4で作れるので二進法では
101100となります
六桁の数字がそれぞれ左から
32、16、8、4、2、1、の数字を表していて
その数字が要るか要らないかを
0か1かで表しているってわけですね
いくつか例を挙げると
3→11
4→100
9→1001
13→1101
19→10011
27→11011
50→110010
みたいな感じです
ここまでついてきてますかー!!
数字が奇数なら右端が必ず1になり
偶数なら0になる、とかもポイントですな
なんか学校の教科書みたいですね
高卒文系野郎がフリーハンドで書いたんで
計算とか間違ってたらゴメンね
(何回か確認したから多分大丈夫なハズ)
はい
二進法が分かったところで
チェス盤にも数字を当てはめていきます
なんですが、、
ここで前述した
『幼女Aの指し手の逃がし場所』
の話に戻りましょう
やはり逃がし場所が必要になってくるのです
つまり盤面上のどこかに
『電源の通ってないバカスイッチ』
を設定しておく事が必要な訳です
さてどうしましょうか
0を使いましょう
0は足しても引いても0です
幼女Aが盤面を触りたくない状況になっても
最初の一マス目に0の数を設定しておけば
そのマスに限っては
ポーンを置こうが取ろうが
0のままでいてくれます
したがって
チェス盤に割り振るべき数字は
1~64でなく0~63が正解です

ここに気付けるかどうかが
この問題の分水嶺とされています
そして0~63を二進法で表記したのがこちら

さてここから見えるのは
それぞれのマスの中に0と1の
六桁の数字があるって事ですな
ここでチェス盤の情報を可視化してみます
このあたりから
実際に紙に自分で盤面を書いて
図画工作してみる事をオススメします
字面で読むだけでなく
自分で手を動かしてみた方が
はるかに飲み込みやすいですよ
というか既に
『書かな分からんレベル』に突入してまっせ

なんかこの六桁のならび
法則性がある気がします、、、
二進法で表した六桁の数字の
右端が1のグループはこいつら

右端から2番目が1のグループがこいつら
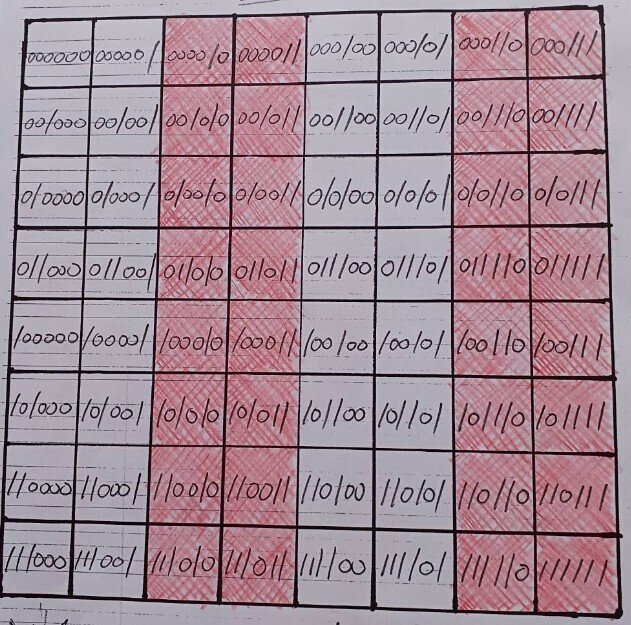
って感じで色分けしてみると分かります
1も3も5も二進法に直すと
右端の数は1ですよね
じゃあ仲間ですよね
4も7も13も二進法に直すと
右から三番目の数は1ですよね
じゃあ仲間ですよね
みたいな理屈を付けて
仲間どうしをグループに分けて
色分けしてみるのです

はい
こんな感じで六枚の塗り絵が出来ました
これをうまいこと使えば
チェス盤の情報を圧縮できないでしょうか
泥水を濾過するように
この六枚のフィルターで濾して
情報を濃縮、抽出できないでしょうか
ためしに悪魔がポーンをこんな感じで置いた
こういう盤面を考えてみます
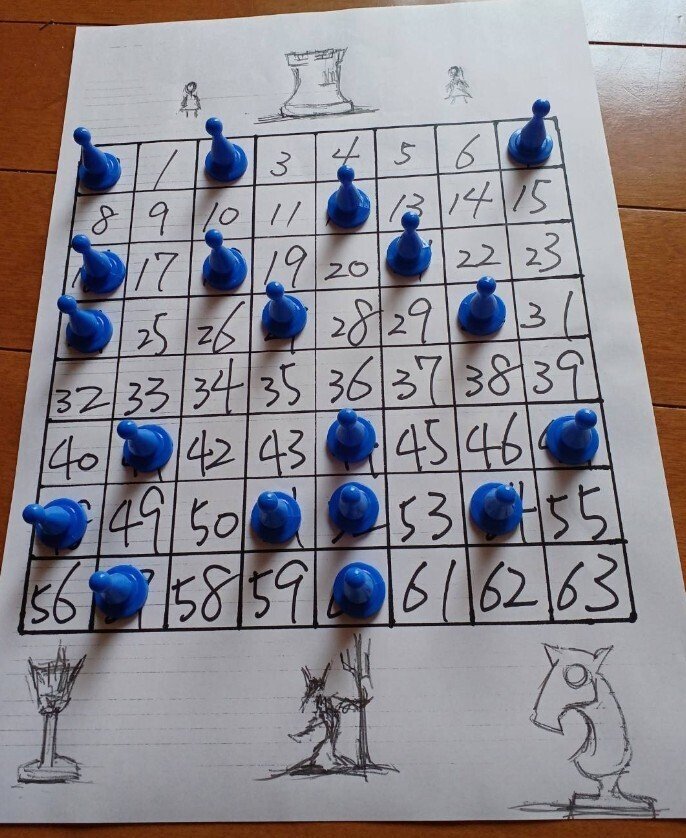
さてこの盤面の情報を
さっきの六枚の塗り絵を使って圧縮します
えーと
どうやるかというと
右端が1のグループはこいつらで

色分けした赤色の上には今
ポーンは7つ乗ってます
右から二番目の桁が1のグループがこちらで

赤色の上には8つのポーンが乗ってます
こんな感じで六枚の塗り絵すべてを
盤面と照らし合わせてみると




赤色に乗っているポーンの数は
9個12個9個9個8個7個となりました
こいつらはあくまで
『なんとなく拾ってみた』だけの
意味のない数字の羅列です
ですが盤面のみから抽出したので
おそらく何かしらの情報は詰まってますよね
というか根拠は盤面のみなので
盤面から得た情報以外の情報を
持ってるわけ無いですよね本質的に
ただまだ数字が大きく
漠然としているので
もう少し情報量を削ぎ落としたいです
さてどうしましょう
そう言えばもうひとつ
オンオフのような
シンプルな二択の分け方がありました、、
そう
前述した奇数偶数です
9・12・9・9・8・7の
偶数を0、奇数を1に置き換えてみます
すると
101101
となりました
どうでしょう
細かい部分を削ぎ落としたこの六桁の数は

この盤面から抽出した情報で構成されており
その情報は濃縮されていると言えますよね
(もちろん偶数奇数で分けただけなので、こうなる組合せは他にも大量にありますけどね)
そして0と1に置き換えてみたこの数値は
別に二進法でもなんでもないんですが
『二進法とみなしてみます』
そしてこの数値
十進法に直すと幾つでしょうか?
計算してもらえれば分かりますが45です
つまりこの盤面から
なんか知らんけど
45という数値が抽出できました
したがって今、盤面は45です
ちなみに奇数と偶数で分けただけなので、盤面の数値が45になるようなポーンの置き方はこれ以外にも当然、無数にあります
が、それでも問題ないのです
ここまで一体何をやっているのか?
今やった事をすごく簡単に説明すると
『三丁目の吉田さんとこのチワワ』という情報を『犬』まで削ぎ落とした感じです
情報は削ぎ落としましたが
悪魔の設問が『何の動物?』だとしたら
それでも間違えてはいませんよね
問題に戻ります
例えば悪魔が今、この盤面で幼女Aに
『26』と告げた場合を考えてみます

その場合
幼女Aが現在のこの45を示す盤面を

26に変える(26を表現する)事が出来れば
同じく六枚の塗り絵を持っていて
作戦を共有しているつまり
『盤面の読み方を知っている』幼女Bに
悪魔が告げた26という数字を
伝えることが出来るはずです
さあチェスがランダムに置かれた
1844京6744兆737億955万1616通りの盤面を
限界までタイトに削ぎ落として
数値化する事はなんとか出来ました
残るは次のハードル
『ポーンひとつを動かすだけで盤面の数字を幼女Bに伝えたい数字に変える』です
45と26
このふたつの数字で
四則演算でもしてみますか
いえいえ単純な計算では無理っぽいです
ここで更なる難関
『その発想なんなん?』ていう
計算方法が登場します
それを使わねばなりません
なんとなく脳内で0と1だけの二進数と
オンオフのスイッチを想像して
0と1の特殊な足し算を想像してみてください
0⊕0=0 両方オフで電気は消えてる
0⊕1=1 片方だけオンで、電気は付いてる
1⊕0=1 同上
1⊕1=0 両方付いてたが打ち消しあってオフ
4つ目だけ普通の足し算と違って
本来なら2になりそうなものですが0です
『打ち消しあう』と理解してもらってもいいし『0と1だけの二進法の世界の話だし2とかは出てこないから切り替わって0になる』と理解してもらってもいいです
要は二進法の世界には
こういう変な計算方法があるよ
ってだけ脳内に入れて下さい
さてさて
二進法はスイッチのようなもの
例えばの話
ここに今、六桁のスイッチが
こういう風に並んでるとして、、

オフのスイッチを全て奥に押し込んで
六つ全てをオンにしたい場合、、
しかもそれをたった一回の動作で
(動かせるポーンは一つだけ、、)
オンにしたい場合、、、
こういう『合鍵』を作って
『エイヤッ!』と押し込めば
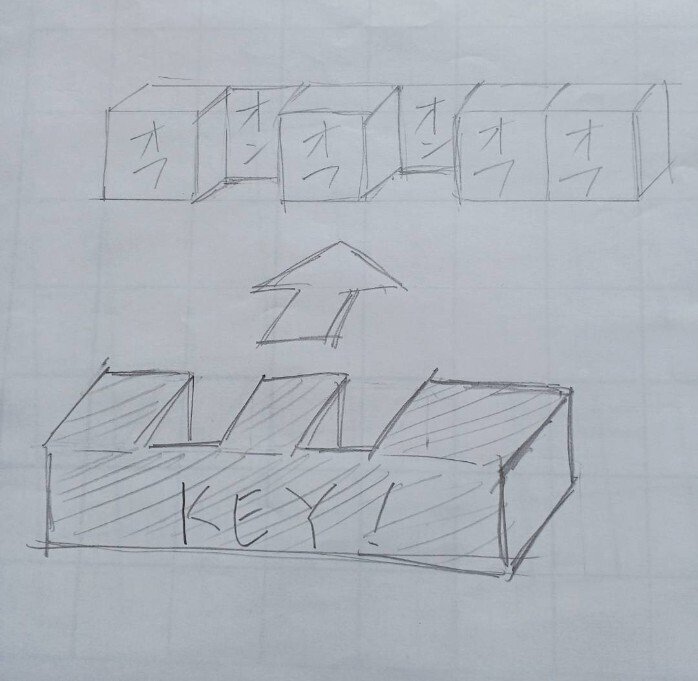
一撃の動作でバチッと一気にスイッチが
切り替えられると思いませんか?
笑えますよね
ほとんど反則ですけど可能ですよね
ではその魔法の合鍵をどうにか作りましょう
45は101101
26は011010
この六桁の数字を一桁ずつ
さっきの計算方法で計算してみます
左端から順番にタテに計算します
こういう事ですね↓

どうでしょう
110111
という答えを手に入れました
そしてこの六桁を
二進法から十進法に戻してみますと
55になりました
この数は45と26という
ふたつの数値を当てはめて
ズレをトレースして得た数字です
それってつまり
ふたつをつなぐ合鍵ですよね!

では55のマスにポーンを置いてみます
(一度きりのアクション、緊張の一瞬です)

はい
ではこの盤面を幼女Bに引き継ぎます
幼女Bは六枚の塗り絵を使って
先程と同じ手順で
盤面から六桁の数字を割り出します

ポーンの数はそれぞれ
10個13個9個10個9個8個
に変わりました
これらを偶数奇数で区別すると
011010
そしてその六桁を二進法に戻します
すると、出ました!
26
確かに悪魔が幼女Aに告げた数です!

解けた!
解けた!
解けたどー!
もしこれが深夜にやってるノイタミナなら
悪魔が咆哮して立木文彦ボイスで
バラバラと朽ちて死ぬシーンです
おめでとうございます!
あなたの勝利です!
最後に補足ですが
さっきポーンを55に置きましたが、もしそのマスに既にポーンが置かれていたら?
どうしましょうか?
答えは簡単です
やる事は同じ
『55のマスのスイッチを切り替える』
のが目的なのでポーンを取ればいいです
要するにポーンの有無は関係なくて
例えば3という数を考えた時、3に1を足そうが引こうが意味は同じで、偶数・奇数の切り替えはいずれにせよ成功するわけです
つまり幼女Aの行う
ポーンの足し引きの動作は
『本質的には同じことをしている』
という事です
補足②
では盤面の数値が45で
悪魔も『45』と告げてきた場合は?
はい
前述したように
『指し手の逃がし場所』
0のマスを使えばOKです

ご覧のように
六枚の塗り絵のすべてにおいて
たった一マス
0のマスだけは赤塗りされていませんので
このマスにポーンを置いても取っても
何ら影響はありません
最後に重要な事がもうひとつ
そもそも悪魔が告げる数字は1~64ですが
作戦に使う盤面は0~63で設定しました
ですから実際には
幼女Aは悪魔が告げる数から
1を引いた数を盤上に作り
幼女Bは盤上から得た数値に
『1を足して答える』
という細かい作戦も必要になってきます
(そうしておかないと悪魔がもしも『64』を告げた時に、そもそも63までしか設定していない盤面では答えを作れないので)
事前に幼女たちの間で『盤面から導き出された答えに1を加えて回答する』という作戦を共有しておくわけです
ここ忘れると
64を引き当ててしまった時に
ケアレスミスで不正解になります
悪魔の最期の息吹き
本当にいやらしいというか
良く出来た最強の問題です
お疲れさまでした
あなたは
二進数とパリティと
排他的論理和(XOR演算)を
理解・消化しました
おめでとうございます
なお、今回のは文系野郎が独学でむりやり咀嚼した数学記事ですので細部がなんか間違ってようが苦情は一切受け付けません
あしからずご了承ください

あ~、疲れた、、
