
JMPで割合の傾向分析を ~高齢者は年齢が上がると、生きがいを感じなくなるのか?~
増川 直裕
本記事では、JMPでカテゴリ(グループ)ごとに割合を比較する方法、割合に関する傾向分析(Cochran-Armitage傾向検定)を実施する方法について述べます。割合を比較する際、JMPではモザイク図という分かりやすいグラフが表示されますので、分析の助けになることでしょう。
例として、内閣府が実施した高齢者に関する調査を扱います。調査対象者に「あなたは、現在、どの程度生きがい、喜びや楽しみを感じていますか」と聞き、その回答を年齢層ごとに分け、生きがいを感じている割合に違いがあるかどうかを調べてみます。
以下の表は、60歳から5歳区切りでカテゴリ化した「年齢」と、「生きがいの程度」に関するクロス集計表をMicrosoft Excelのピボットテーブルで作成したものです。
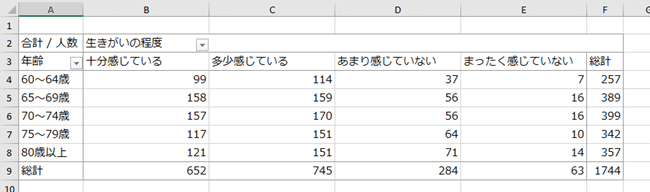
データの出典:内閣府 令和元年度 高齢者の経済生活に関する調査結果
※実際公表しているのは各年齢のデータ数と、生きがいの程度の各回答に対するパーセンテージだが、上記の表は筆者の方でデータ数とパーセンテージから計算した度数。四捨五入の関係で、実際の度数とは若干異なる可能性がある。
※回答には「不明・無回答」というカテゴリがあるが、便宜上、このカテゴリは除外して考える。
アンケートなどの調査では性別や年齢、所得など、回答者の属性に分けたときの回答状況を知りたいため、よくこのようなクロス集計表が作成されます。
クロス集計表は上記のように、各セルに属する人数が表示されているものもあれば、属性ごとの回答の割合が表示されているものもあります。いずれにせよ、集計対象となるカテゴリ数が多い場合は、大きなクロス集計表になり、属性ごとの回答割合の違いを調べるのは大変ですし、見ているだけで頭が痛くなります。
筆者も、以前の業務で、ものすごく大きい(カテゴリ数が多い)クロス集計表を延々と作る作業をした経験がありますが、
こんなもの作って意味あるのか? こんな大きな表を手間かけて考察する人がいるのか? と思いながら作業していた記憶があります。
以下では、クロス集計表の分析に関して、JMPではどのようなアプローチができるのかを解説します。
■JMPの「分割表分析」
分析対象となるデータは、次のように入力しています。
2つの変数「年齢」、「生きがいの程度」 があり、各行に該当する人数を「人数」に入力しています。

例えば1行目だと、60~64歳で生きがい程度を”十分感じている” と回答した人が99名いることを示しています。
年齢の違いによって、生きがいの程度の回答割合に差があるかを知りたいわけです。このときJMPでは、”2つの変数 「年齢」と「生きがいの程度」の間に関係があるかどうか” を分析したいと考えます。
2つの変数の関係を考える とき、JMPでは「二変量の関係」 というプラットフォーム(機能)で実施できます。

「二変量の関係」で、次のようにY, X, 度数の列を指定します。

「二変量の関係」は、Y,Xに指定した尺度に応じて、その尺度に適した分析結果が出力されることが特徴です。
今回の例では、Y,Xともに名義変数(質的変数、カテゴリカル変数ともいう)が指定されています。このときは、上図の赤枠で囲った「分割表」のレポートが表示されます。
表示されるレポートは、「モザイク図」、「分割表」、「検定」の3つで構成されています。最初に「モザイク図」というグラフが表示されるのは、JMPらしいところです。

この3つのレポートでクロス集計の分析をより深く、分かりやすく考察できるのです。そこで、これらのレポートを順に解説します。
モザイク図
近年、この「モザイク図」が割合データの可視化手法として市民権を得ているように思えますが、JMPでは、市民権が得られていない(?)かなり前から搭載されているグラフです。

右側の細長い棒は、Y(生きがいの程度)の割合を示したグラフです。一般的には帯グラフと呼ばれています。
Yの割合を、X(年齢)ごとに分けたらどうなる? ということを分かりやすくグラフ化したのが、モザイク図です。
横軸が年齢、縦軸が対する生きがいの程度の割合を示しています。
横軸は年齢の割合に比例するように幅を定めています。この例では60~64歳の幅が他の年齢に比べて小さくなっているので、このカテゴリのデータが他のカテゴリに比べて少ないことがわかるのです。
縦軸は生きがいの程度の回答割合を示しています。上図では解釈をしやすいように、モザイク図を右クリックして [セルのラベル] >[パーンセントラベル] を選択し、モザイク図のセルにパーセント(割合)を表示しています。
分割表
いわゆるクロス集計表です。各セルには4つの数字が表示されていますが、上から順に、度数、全体%、列%、行% を示します。

モザイク図で示している割合は、最後の行に示している「行%」です。つまり、年齢で分けたとき、それぞれの年齢における”生きがいの程度” の回答割合を示しているのです。
検定
最後は検定のレポートです。ここでは、”X(年齢)間で、Y(生きがいの程度)の構成割合に差がない” という(帰無)仮説に関する検定結果です。よく、「ピアソンのカイ2乗検定」と言われる検定に相当します。
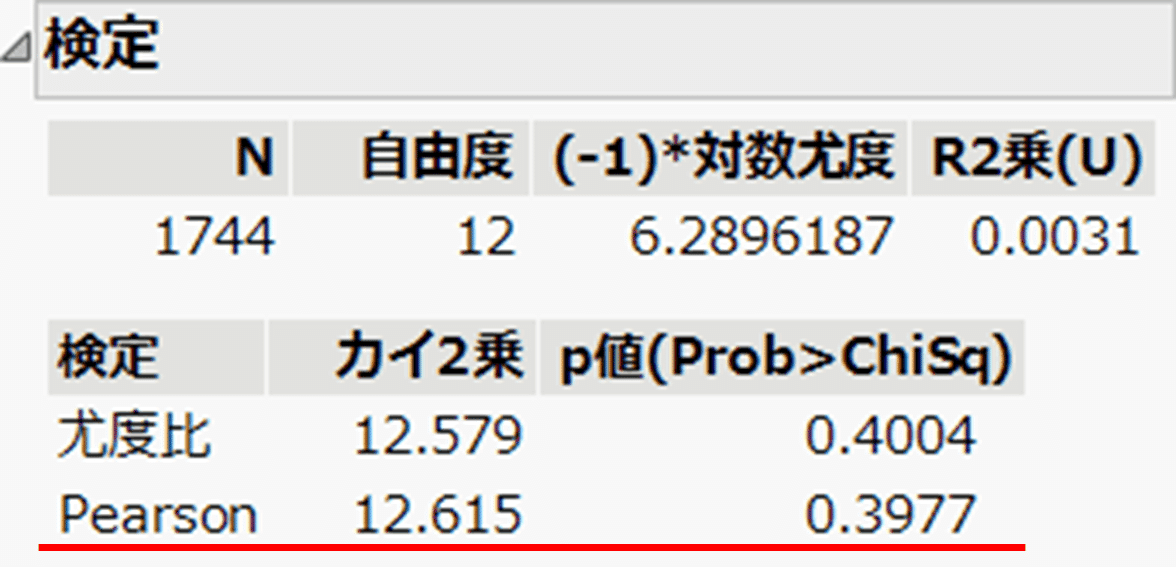
赤線を引いた箇所が、ピアソン(Pearson)のカイ2乗検定の結果です。 有意水準を0.05とすると、p値は0.3977と0.05より大きいため有意ではありません。
そのため、モザイク図を見る限りは年齢間で生きがいの程度の割合に若干の差が見られますが、統計的な有意差はない、つまり”差があるとはいえない” のです。
■割合の傾向をみる Cochran-Armitage傾向検定
上で示したモザイク図をみると、”年齢が上がるごとに生きがいを感じる割合が減少する” ように見えますが、統計的に考えると果たしてどうでしょうか?
この点に対して、内閣府の調査では、回答結果から次のように2つのカテゴリ(感じている、感じていない)に分けて集計が行われています。
十分感じている、多少感じている ⇒ 感じている
あまり感じていない、全く感じていない ⇒ 感じていない
このようにカテゴリをまとめたときのモザイク図を示します。

モザイク図をみると、70~74歳は、65~69歳に比べ生きがいを感じている割合が0.5%ほど高くなっていますが、全体的には年齢が上がると、生きがいを感じている割合が減少する傾向にありそうです。
それを統計的に裏付けるために、Cochran-Armitage傾向検定を実施してみます。
Cochran-Armitage傾向検定を用いると、順序性がある変数「年齢」に対し、年齢が上がるにつれて、生きがいを感じていると回答した割合が有意に減少しているかを調べることができます。この検定の(帰無)仮説は、”傾向がない”です。仮説が棄却されれば、傾向があるといえます。
JMPでは、分割表分析のレポート左上の赤い三角ボタンから [Cochran-Armitageの傾向検定] のオプションを選択すると、分析レポートにこの検定結果が追加されます。

注意:この検定が実行できるのは、Yのカテゴリ数が2つのときのみです。カテゴリ数が3つ以上の場合、このオプションは表示されません。
こちらがレポートです。 2種類のp値(片側検定、両側検定)が表示されていますが、減少傾向または増加傾向をみる検定のため、通常、片側検定のp値(Prob < Z)を参照します。

p値は0.0086となっており、0.05より小さいです。そのため仮説が棄却され、割合の傾向性がいえます。
すなわち、年齢が上がるごとに、生きがいを感じている割合が減少する傾向( = 生きがいを感じていない割合が増加する傾向)が統計的に示されたのです。
とはいっても、80歳以上でも、4人に3人以上が”生きがいを感じている” というのはすごいことだと感じます。年齢が上がるとともに、自身の病気や配偶者の死別など、さまざまな要因で生きがいを感じられなくなりそうな気がしますが、高齢になっても、ずっと生きがいを感じていられる生活が望ましいですね。
■JMPの特長、基本機能、操作を学べる無料オンデマンド動画
■JMPトライアル版
https://www.jmp.com/ja_jp/download-jmp-free-trial.html
