
英語力の高い小学生は中学受験に向いていない?英語力が高い小学生や中学生の大学受験に向けた数学対策。理屈っぽい日本の数学の授業は苦痛でしかない。
以前私が投稿したブログを紹介していただいたようです。
このブログです。
現在中学1年生(当時小学6年生)の生徒に教え始めて1か月経ったときのブログです。
実は、この記事は、英語力の高い生徒は、中学受験するよりも、小学生の間に中学生の数学の範囲をすべて学んだ方が絶対にいいよね。という意図で書いたわけではありません。
女子生徒の場合は、どうしても数学の中でも、得意な分野と不得意な分野が男子生徒に比べて表れやすい。特に英語力の高い生徒に関しては、読書量が多く、感受性が豊かである反面、非言語の数学の可視化しにくい問題文は苦手な生徒が多いと感じます。
ですので、小学生6年生の時に、イギリスのGCSEのテキストを使ったり、IBのテキストを使って、その生徒の得意分野と不得意分野を把握するだけでなく、不得意分野の細かな分析をして、数学の大学受験に対応できる準備をしたかった。
というのが意図でした。
英語力の高い生徒や海外留学を経験した、または、留学する予定の生徒に共通する傾向があります。それは、中学1年から2年に数学の成績が一気に下がって、英語の成績が上がる。特に男女共学の学校に通っている生徒では顕著です。
ですので、小学生や海外留学を希望している生徒には、数学の従来のカリキュラムに縛られる必要もないので、小学生に中学や高校で習う数学の基礎的な問題を主にGCSEのテキストを使って教えているわけです。
もう一つ理解してもらいたいのは、英語が得意な生徒は、数学が苦手な生徒が多く、これは英語力が高くても低くても例外は非常に少ないと思います。この主な原因の一つは、数学が非常に理屈っぽい教科で、感性で英語力を伸ばした生徒にとっては、数学が得意な人には木にならないことも、気になってしまうわけです。
例えば、数学の一次関数のグラフの勉強で直線の傾きを求める問題があります。
2点の座標が決まっていて、そこから傾きを求めるわけです。
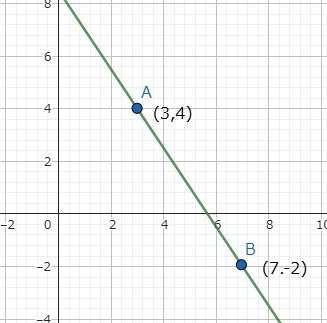
それぞれの座標をそれぞれ下記のようにa,b,c,dとします。

学校では傾きを求める場合、このように教えます。

これが意外にも理解できない生徒が多いわけです。

そうすると、このように、縦書きで説明すると、理解してくれる生徒は多くなります。それほど違いがあるように感じないかもしれませんが、このような微妙なところに数学が苦手になる落とし穴が隠れているわけです。
現在高校1年生の生徒は、中学生の時に家庭教師を始めたのですが、ちょうど二次方程式の解をたすき掛けで求める授業をしていたので、私が普段から小学生や中学生に教えている別の解き方を教えました。
そうしたら、すぐに理解してくれて、その後の平方完成などもスムースに解けるようになりました。数学が得意でできる人には気にならないようなことでも、数学が嫌いになった人の多くは、少しだけ違った説明をその生徒に合わせて教えていれば数学が苦手科目ではなくなって、医学部や工学部を目指していたかもしれないと思うと、大げさではなく、人生の大きな分岐点になっているわけです。
三角関数が数学を伸ばす大きなステップになる。
海外の高校で学んでいる生徒も日本の高校で学んでいる生徒も、三角関数が数学を得意教科にできる大きなチャンスだと私は考えています。
三角関数はユニットサークル(unit circle)を理解することが大切。
三角関数は、多くのidentitiesを覚える分野で sin²θ+cos²θ=1のようなアイデンティティーをはじめ、二倍角の公式や和積の公式など覚える公式が多いと思います。
そこで登場するのがユニットサークルです。

こんな感じですが、このユニットサークルを使うことによって、sin60°とcos30°の値が同じことも、sin30°とsin150°の値が同じことも理解できると思います。
また、sinθをyとして、cosθをxとして説明をすることで、ユニットサークルを使うことでややこしさを相当軽減することも可能だと思います。これを応用すれば、例えば、正射影ベクトルの説明もわかりやすくなりますし、そこから、クロスやドットのプロダクトの説明も理解しやすくなります。
ですので、小学生や中学生で今後医学部や工学部、理学部などに入学を希望する生徒に対しては、最低でも三角関数を教える基礎を固めるために、どうしても、小学生や中学生の期間に選考学習をして、学校のカリキュラムとは違った教え方をしていかなければならないわけです。
数字に強くなるためには、苦手分野は早めに手を打って、対応するためにも早い時期に教えられるのであれば、繰り返し学ぶことができるのでメリットは高いと思います。

このような3問。時間をかければ解ける問題だと思いますが、できるだけ早く解くためにはどのような準備をしなければならないかに関して説明します。
一番は√3=1.732 なので、√3/2は0.866くらいと考える。
日本の場合は、欧米の数学と違い計算機を使わないために、√3/2は計算して、0.866にしないで、そのまま√3/2で答えとします。
そうすると、√3/2が小数点にすると、いくつかがわからないわけです。これが日本の数学の難しいというか、おかしなところです。ですので、三角関数の応用問題で角度を求める場合も、答えは30 45 60関連の角度しかなくて、あっても、15 75が限界です。
凄く制限された中で学ぶので、その窮屈な数学ではなく、海外のテキストで学ぶことはストレスを無くしてくれると思います。
また、6/7は約0.857です。1/7は約0.143なので、6/7は1-0.143=0.857と計算するのが大切です。
2番のじゃんけんの問題は、普段の生活の中の一部を数学的に考える勉強だと思ってください。
細かな数学的な説明は、解説なしで、まず4人がじゃんけんで出すのは全部で3x3x3x3で81通りです。それに、全員が同じものを出すのが、ぐー、ちょき、パーの3通り、4人中2人が同じで、残りは別のものを出す場合、例えば、2人がグー、一人がチョキ、一人がパーのような場合が、4人だと、4x3x2÷2で12通り、それにグーチョキパーの3通りをかけて36通り。
ですので、答えは3+36/81で13/27になります。
確率は、数学の中でも日常生活に非常に近い分野です。ですので、アルファベットやノーテーションで考えるのではなく、イメージして考える力を付けさせたいわけです。
数字で考えるのは最後の仕上げだけでいいので、その過程をしっかりと理解してもらえるようにしてほしいわけです。
確率が本当に苦手な生徒は多いので、このような少しだけ複雑にした確率の問題をしっかりと一つ一つを理解しながら解くのは大切です。
最後の三番の問題は、効率的に解くための機転を身につけるための問題です。
The least number of 5 digits which has 123 as a factor is?
A)10025 B)10042 C)10067 D)10086
意味は、5桁の整数で123の倍数の中で一番小さい数はいくつか?
123は素因数分解すれば、3x41となります。ですので、それぞれの数が3で割れるか考えてみます。
それぞれの位の数を足して3の倍数になったら3で割れることになります。この場合、Dだけが割れますので、答えはDになります。
この問題は簡単な問題ですが、例えば、
√a²+40で、aは自然数だとすれば、この答えが自然数になるのはaがいくつの時か?すべて答えよ
のような問題なども作れるわけです。
(√n²+40)²=m² から式を変形して、n²+40=m² ⇒m²-n²=40
(m-n)(m+n)=40で、
(m,n)=(7,3) (11,9)が答えになります。
数学の先行学習は必要か?
現在、中高一貫の学校では、早い学校では高校1年生ですべての数学を終えて、残りの2年間は受験に備えた数学の勉強をするわけで、中高一貫校ではほとんどの学校は高校2年生までにすべて終えてしまいます。これでは、高校受験をする人たちは本当に不利になってしまいます。
これも、先行学習となるわけです。
数学と英語の違い。
英語力が高い生徒は、英語圏の英語のテストで高得点を取れる。
英語が話せても、英語の理解力が高いかどうかは別の問題です。つまり、海外で生まれ育った日本人やミックスの人は英語力が高いのは当然ですが、その人たちがアメリカのSATの英語でみんな700点以上取れるかと言えば、そうではありません。
日本の共通テストの現代文で満点近く取れる人もいれば、ほとんど不正解の人もいます。両者とも日本語を不自由なく話せます。英語の場合は、流暢に話せると言っても、そのような二面性があるので、本当に難しいわけです。
一方数学は、国籍や育った国などにより有利、不利がありません。
ですので、私の中では、現状で数学の学力が十分であれば、どんどん先行学習をして、上のレベルを目指すのは問題ないと思いますが、そうでないのに、先行学習をしてしまっても意味はないような気がします。
ただ、英語力が高い生徒は、例えば空間図形、証明問題、確率、グラフ問題など数学の苦手な分野が多いのも事実です。
特に、高いレベルの大学を狙う生徒にとっては数学を他の人よりも先行して学ぶことは大学入試を有利にすることになると思います。
私は、そのような生徒に苦手な分野をじっくりとケアする時間が必要なので、先行学習は数学は暗記科目ではないので合格するためには不可欠な対策だと思います。
