
来年のA-Levelのfurther mathematics のA*を確実にするための最後の夏休みの集中特訓終了。計画的な準備が本当に大切な理由。
7月8月2か月弱、来年のA-Levelの受験を控えた生徒の夏休みの集中特訓が今日で終了予定です。
日本にいた4年以上前から数学を教えていたので、振り返ると成長の跡を感じる瞬間が増えてきて頼もしくも思います。ヨーロッパ留学の生徒の場合は、時差の関係で週末しか教える時間が取れません。
この2か月で、ベクトルと複素数平面をみっちりやってきました。
ただ、vectorはこんな感じだよ。Complex numberはこうして解くんだよ。
という話ではなくて、分からない問題が出題された時にどのように対応していけばいいのか?そのために、どんな対応をしなければいけないのか?
この後に、polar coordinate, hyperbolic function, first, second order differential equations とさらに高いレベルが控えているので、基礎をしっかりと固めるための2か月にしたいと考えていました。
高いレベルになればなるほど、今までどのような勉強をしてきたのか?identitiesをどんな状況でも適切に応用できるのか?
暗記で覚えるのではなく、型にはまらない、今まで学んだidentitiesを使って証明できるように。
そのような瞬時の応用力が、インタビューでは問われます。
これは教えてどうにかなるものではなく、ヒントを与えて、それを生徒がどのように吸収するのか。ということが大切になるわけです。
今日は、日本では数学Cで学ぶ複素数平面を、日本の堅苦しい意味不明な数学用語だけでなく、英語の説明も交えて、難しい問題でも、楽しみながら覚えるにはどのように数学に向き合ったらいいのか?ということにこだわって伝えていければ。と、考えています。

あくまでも数年後に複素数平面を学ぶだろう人の中で、英語を学ぶことが好きな人で、日本の数学先生あるあるの理屈っぽい教え方にアレルギーのある方のみ伝えているので、ご理解してください。
複素数平面って何?
複素数って、素数が複数あるってこと?
としか、思いつきませんよね。
それに平面って?加えてさらに何が何だか??複雑になるだけです。
こんな感じです。

よくわからないですよね。
しかし、これから複素数平面を学ぶ中で、
複素数平面を complex number
正のx軸(Re)から、時計回りの反対の角度をargument
argumentという言葉はcomplex numberで使われる言葉です。
絶対値 つまりこの表ではOPの長さをmodulus
Modulusもcomplex numberで使われる言葉です。
Complex numberはz= a + biで表すので、表の座標(coordinates)と言います。は、(1,√3)となります。
直角三角形(right angled triangleまたは、right triangle)を作れば三角定規と同じ、30度、60度、90度ができるので、θは、60度になります。また、complex numberの時は、πを180度として考えるので、直径x円周率が2πなので、それを360度として計算しているので、60度はπ/3となります。
ですので、この直線の式をpolar formと言って、OPの長さが三平方の定理(Pythagorean theoremと言って、ピタゴラスという発音よりも、どちらかと言えば、パイサゴリアンとなります。
1²+√3²=x²なので、x=2
なので、式はz= 2(cos3/π+ i sin 3/π)
となります。

では、質問です。
今までは、座標はx軸、y軸などと言っていましたが、今回はx軸がReで、y軸がImとなっています。それぞれ何の略だと思いますか?
これは、
Z= a + bi の式ですので、実数がaで純虚数がbiで、二つが合わさって、complex numberというわけです。ですので、実数を英語ではreal number 純虚数をimaginary numberと言って、合わせてcomplex numberつまり複素数となるわけです。
この式はz=r(cosθ+i sinθ)で、表せますが、euler’s relation を使って、

とも表せます。
このθの角度を180度にして、つまりπにすれば
数学が好きな人が美しいと絶賛する
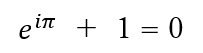
の式が導けるわけです。
これは、
Substituting θ=π into Euler’s relation yields Euler’s identity:

This equation links the five fundamental constants 0,1,π,e and i , and is considered an example of mathematical beauty.
数学の基本となる、0,1,eπ,i の5つを方程式で表現できるので、数学の美しさを伝えるわかりやすい例として登場するわけです。
だから何?
と今は思うかもしれませんが、理解できるようになると美しく見えるわけです。
また、このexponential formを利用して、掛け算や割り算をすると、簡単に計算できるわけです。

De Moivre theorem

ドモルガンの定理を使ってもいいですが、こっちの方が簡単にできます。

割り算をexponential formで計算すればこうなります。
簡単にウェブ上だけで伝えるとよく意味が伝わらないことは十分に承知しています。しかし、これを一緒に勉強すれば複素数の知識がなくても、ある程度分かるようになって、その中で基礎を固めることが大切だということがわかってくれるわけです。
A-Levelのfurther mathsは今までやってきたGCSEの勉強がどれだけしっかりと理解できたのかが試される試験だということがわかってくれればうれしいです。
つまり、公式を覚えて問題を解くだけでなく、公式が深く理解して、しっかりと公式が成り立つことをいろんな形で証明できるレベルの数学力が必要になるわけです。
常に自分が今行っている数学の勉強が将来どのような形で大学受験に出題されるかを理解して学んでいけば、これからどのように勉強に取り組んでいけばいいのかがわかってくれると思います。
海外の英語圏の大学入試は、ローカルだけでなく、中国人、インド人、ヨーロッパのレベルの高い生徒が集まって来るわけで、日本人には理解できないかも知れませんが、留学をして学力が付けば海外の大学の理系学部で学ぶ楽しさにあこがれてしまうわけです。
いろんな選択肢があって、好きな進路を選ぶことのできる時代になりました。
英語力を付ける中で、数学の重要性に気づいて進路を決める時代になってほしいと強く感じます。
