
クイズ感覚で数学の問題を解く 出題する4問のバランスを吸収してほしい。アメリカのSAT数学っぽい問題。
数学を教える場合、どうしても生徒によって、また問題によって、解く時間は異なってしまいます。また、時間配分は生徒に合わせて計画するのですが、完璧に行くことばかりではありません。
つまり、あと5分しか時間がないときに、次の問題を出題したくても、解説なども含めると10分以上予定終了時間を超える気がしたら、別の問題を出題するしかないわけです。
そのような場合は、その生徒にとってあまり難しくない問題で、例えば数か月前に教えて、少し忘れかけている対数指数の問題を視点を変えて出題したり、三角形から円の半径を求める問題で、円の中心を通る直線と円周角から相似の三角形を作りだすような発想力を必要とする問題を出題したりして、時間を有効に使うようにしています。
今日は、今まで生徒に出題したクイズ形式の問題の中の4問を出して、出題ポイントも含めて書いていきたいと思います。
最初の問題は

小さい順に並べる問題です。
ちなみに英語では、Arrange the following in ascending order.これから留学をする生徒や海外の数学の授業を受けたことの無い生徒には数学用語や表現を教える意図もあります。
これは、例えば、
√3−1と、0.5(1/2)はどちらが大きいかを理解しなければならない場合に、正確で、かつ、素早く解くための練習です。
写真の問題のように、+や−の符号がない場合は、整数の部分をルートにして、すべてルートにして大小を比べればいいわけです。
つまり、3√3=√27、2√7=√28、5=√25となり、
答えは
5 < 3√3 < 2√7となります。
時間を十分与えれば正解してしまうので、10秒以内のように時間を決めて出題することが条件になります。
また、+や−の符号がある場合は、実数で計算します。それほど細かく計算する必要もないので√2は1.4、また、√3は1.7で計算すれば十分です。
次の問題は指数計算の問題です。
まず中学生レベルの問題から

数の大きさに騙されずに考えれば問題ないのですが、このような問題は解けない人が案外多い問題です。
2¹⁵ は、2³ × 2¹² と考えればいいわけで、
8×2¹²=32,768 なので、32,768÷8=4,096 となります。
高校レベルの問題はこちらです。

log2=0.3010と、log3=0.4771は暗記レベルで、
対数のアイデンティティーで有名な
log5=log10/2=log10−log2=1−0.6990 で
log2を0.3、log3を0.48、log5を0.7にして、
log2²⁰=20 log 2で、6
log3¹²=13 log 3で、6.24
log5⁹= 9 log 5で、6.3
と、なるので答えは
log2²⁰ < log3¹² < log5⁹ となります。
対数のアイデンティティーをしっかりと応用できるようにしてほしいわけです。以前、指数対数を教えて、3か月経った時に、この問題を出したら解けなかった生徒がいましたが、このことがきっかけでしっかりとアイデンティティーを理解してくれました。
次は図形の問題です。

典型的な30秒問題です。
15度75度90度の直角三角形の比は√6+√2 : √6−√2 : 4知っていれば、そこから始めてもいいし、頂点Cから辺ABに30度60度90度のスペシャルアングルを作って、残りを15度15度の二等辺三角形にして、比はこのようになります。

最後の斜辺の長さは8+4√3を8+2√12にして二重根号を外して√6+√2となります。
ただ、面積が1cm²となっているので、自動的にxy=2となり、
そうすれば、自然と
(√3+1)(√3−1)=2
が思いついて、自然と斜辺も2√2となり。
答えはx=√3−1 y=√3+1 z=2√2 となります。
これは、典型的な30秒問題です。
そうして、最後の問題がこれになります。
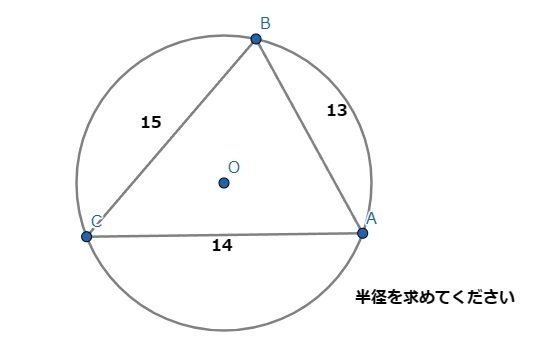
この問題は、中学校の数学の知識で解ける問題です。
この問題のポイントは2つあります。
一つ目は
まず、斜辺が15と13と考え、整数比の直角三角形が思い浮かびあがりませんか?
15は3:4:5の直角三角形であって、13は5:12:13の直角三角形です。

大学受験の数学には、問題を見て、解き方を予測して解かなければならない問題が出てきます。
そして、円に外接する三角形の半径を求めるわけですから、直径を中心角にした円周角から直角三角形を作る。つまり、∠G=∠Aとなるわけです。

そうすると、⊿BCGと⊿BFAは相似となり
15:12=X:13となり
X=65/4 で、Xは直径なので
半径は半分の65/8または8.125となります。
ごちゃごちゃしてきて、何が何か少しわかりにくい面もあると思いますが、今回言いたかったことは、
効率性を向上させるために生徒が学ばなければならないことはたくさんあるということ。
私の学生時代は、やたらと先生は勉強時間を増やせ、過去問などをバンバンやれ、と、まさに昭和時代の非効率の象徴のようなお言葉を投げかけてくれました。
オーストラリアやイギリスやアメリカやインドの数学の問題の中にも本当にいい問題はたくさんあります。そのような問題を有効に使うことによって、どんな教え方をするのが生徒にあっているのかを考えることができます。
日本の数学の問題は本当に理屈っぽい表現が多く、そのうえ、英語を強引に日本語にした数学用語が多いので、理屈っぽいことが大嫌いな生徒は本当にかわいそうだと思います。
現在教えている中学3年生の生徒が通っている学校の数学の期末テストが終わりました。
二次不等式の問題で、xの範囲がa≦x≦a+1のような問題で、xの範囲に応じて最大値と最小値を求める問題です。大量脱落者を出す範囲です。
女子中学校ということもあって、赤点続出だったそうです。
こんなことは、毎年の恒例行事であって、本当に対策を立てなければならない範囲であるにも関わらず、全く対策を立てない授業を毎年行っているようです。
ここで、多くの人が文系学部への進路変更をするわけですが、本当にもったいないような気がします。
数学ができないだけで、本当はやりたい研究を学ぶことも出来ずに、営業の仕事をしなければならないわけです。
英語が好きな人は、数学も伸びるはずなのにもったいないばかりです。
この記事が気に入ったらサポートをしてみませんか?
