
中学受験をしない小学6年生の数学の勉強(5か月目)平方完成と因数分解Hence, or otherwise を理解して問題を解く
中学受験や高校受験など、同級生と競争しながら偏差値や得点を上げるために勉強するのではなく、海外に目を向けて、日本からの視点ではなく、グローバルな視点で考え、外国人とコミュニケーションを取るために英語を学び、大学での専門的な勉強や将来の就職に備えて、論理的な思考を身につけるために数学をテストのための勉強ではなく、自分のペースで知識を詰め込む教科ではない非言語科目として学びたい。
という考えの家庭もあると思います。
現在小学校6年生の生徒に教えている数学の勉強が、現在中学受験のためにハイレベルな算数を学んでいる生徒たちと比較して、同じように見えているかもしれないけど、本当に少しだけ違う勉強ということを伝えられたらと思っています。
今回は中学受験をしない小学6年生5か月目ですが、合わせて、中学受験をしない小学6年生4か月目。を読んでいただけたらと思います。
5か月目は時間をかけて、二次方程式や二次不等式などの因数分解と二次方程式からの平方完成で、二次方程式のグラフを理解する。
二次方程式や二次不等式で解を求めるために、普通のx²+3x+2=0のような基本的な問題だけでなく、解の公式を使って、ルートを含む解のある問題を解いたり、判別式を使って、実数解なしの二次方程式、x²+2x+5=0のような問題を解いたりしたうえで行うのが、
ax²+bx+cで、aが1ではない場合かつbがaで割り切れない問題の平方完成
まずは問題です。
Completing the square when a is not 1
Write 2x² + 3x + 2 in the form a(x + b)² + c where a, b, and c are rational numbers.
Hence, or otherwise, write down the coordinates of the turning point of the graph of y = 2x² + 3x + 2
x²の係数が1ではなく、かつ、xの係数がx²の係数で割り切れない二次関数の平方完成は面倒ですし、間違いやすいですよね。
しっかりと、簡単な平方完成で基礎的なことを学んだあとで、このような間違いやすい平方完成の問題に時間をかけて平方完成を理解してもらいたいと思っていました。また、この平方完成をグラフにすることによって、因数分解の解はyが0の時のxの値であり、平方完成をすることによって、そのグラフの頂点を求めることができるということを理解してもらいたいわけです。
もちろん簡単には理解してもらえないので、何度も類題を解くことによって、少しずつ理解してもらうようにして教えました。
基本はこんな感じです。
In the standard format (まず左辺にすべての項を移動します。)

Take out a factor of 2 (2を共通因数にしてかっこの外に出します。)

Write out the initial bracket (かっこの中を平方完成します。)
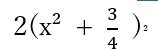
Multiply out the bracket (平方完成した式を展開します。)


Compare to the original
And add on adjusting number(元の式とそれぞれの係数を合わせます。)

Complete square form is (平方完成が完成しました。)

まずこのように平方完成をしたうえで、今度は頂点を求めます。
このようになります。
Complete square form is
2(x² + 3/4)² + 7/8
The minimum point occurs when the brackets are equal to 0.
This will happen when x = -3/4
At this point, the graph takes its minimum value,
Which is the adjusting number of 7/8
The adjusting number is positive, so the graph will never cross the x-axis.
まず、先ほどの問題の平方完成の答えが

となります。
aが正の数なので、最小値はかっこの中が0になる数になり、xが−3/4の時になります。
そして、xが−3/4の時にyは7/8となります。
つまりこのグラフはこのようにx軸と交わらないグラフとなります。

このように実際にグラフで示すことによって、平方完成や因数分解をグラフで表すことで、可視化できるということです。
Hence, or otherwiseをしっかりと理解する
高校数学を学び始めると、問題にHence, or otherwideが含まれる問題が非常に増えます。これは日本でも海外の数学の問題でも同様のことが起こるわけです。
Hence, or otherwiseは前の問題を解いたことを踏まえて、この問題を解いてもらいたい。けど、別の方法があれば別の方法で解いてもいいですよ。
と、日本人には理解しがたい挿入句になります。
ただ高校数学になれば、解き方は2つ以上あることが普通で、答えは一つであっても、問題を解く過程はいくつもあるわけです。
他の生徒に数学を教えている時に、このHence, or otherwiseを含んだ問題があったので参考までに掲載しておきます。代数の問題です。

まず、aはtがxの3分の1乗だとしたら、xの3分の2乗をtで表したらどのようになりますか?
bはaの問題を利用して方程式を解いてください。
という問題です。
ここに、Hence, or otherwiseが登場しています。
解答はこちらになります。


本当に基礎的な指数関数の問題です。
この問題の単元になる指数と対数をいつこの生徒に教えるかまだ未定ですが、できるだけ早い段階で指数と対数を一緒にして、難しい問題を出題しないで、このような基礎的な問題で教えることができればと思います。
計算問題を中心に応用問題を極力出題させない理由。
この小学6年生の場合は、女子特有の若干の図形、グラフアレルギーがあるために、計算問題を中心に出題して、しっかり理解した上で、高校数学のレベルの問題から応用問題を出題したいと考えています。
それぞれの生徒にはそれぞれの個性がある。その生徒の長所を最大限に生かす教え方。
私が教える生徒は、全員が結果的に留学に関心がある生徒、または、実際に現在留学している生徒になります。
この小学6年生も小学5年生の時に英検1級を取得しているように、英語を単に理解しているだけでなく、私が説明する少し小学生では複雑に感じる説明をしっかりと理解してくれています。
応用問題が苦手な生徒は、文章理解力が弱い生徒が多く、国語力のある生徒は比較的応用問題は苦手にしていない場合が多く、仮にわからなくても基礎をしっかりと教えておけば、わからない応用問題も、説明すれば早い時期に吸収してくれますので、無理に応用問題を教える必要はないということです。
代数が終わったら何を教えるかはまだ決まっていません。
現在平方完成が終わって、連立方程式を教えているところですが、その後、勢いで、三角関数や三次関数、円などのグラフを教えながら円や、三次関数を教えるか。三角関数のSOH CAH TOAを教えているので、余弦定理や正弦定理を教えるのか、現在考え中です。
このように、学校の授業のように、決められた指針に合わせて学ぶのと違い、その生徒の個性や長所を生かした教え方をすることで、ストレスを感じさせないで、無理なく教えることが出来たらと考えています。
この記事が気に入ったらサポートをしてみませんか?
