Pythonの深層学習でイーサリアムの価格変動を分析・予想する
投資先の仮想通貨(イーサリアム)がまた下がった。10月頃は5月の大暴落を乗り越え、年末年始に100万円を超えるという意見もネットでは散見されたが、ブログを書いている今も暴落を続け現在20万円代にまで下落している。
仮想通貨バブルはもうこれで終わりであり、電子ゴミとして処分するべきなのだろうか。それとも仮想通貨は今後も上昇継続を続け、今はまたとない絶好の買い場なのだろうか。その瞬間の感情に委ねると大体失敗する。
仮想通貨の特徴としては市場がまだ未成熟であるため、株よりもテクニカル分析が有効である点が挙げられる。チャートの形状が明確なシグナルを描いた時、極端な買い注文あるいは売り注文が世界中から殺到する。
このような性質から過去のデータから価格変動を学習し、チャートパターンを見出すことで、ある程度の予測が人工知能で立てられるのではないかと考えた。
分析フロー
分析フローは以下の通り。
① 取引所から過去の価格変動を取得
②価格と変動率の推移をグラフ化
③時系列解析における入力データの設定
④変動率のラベリング
⑤予測モデルを構築し、予測精度を計測
⑥クラス数の調整とクラス毎の重み付け
⑦レイヤー層と各パラメータの調整
⑧乱数seedを変更して確認
⑨まとめ
① 取引所から過去の価格変動を取得
coin = "https://api.cryptowat.ch/markets/bitflyer/ethjpy/ohlc"
# periods・・・指定した秒足のデータを取得 ※日足は86400 週足は604800
day = "?periods=86400&after=0000000000"
df_columns = [
"CloseTime",
"OpenPrice",
"HighPrice",
"LowPrice",
"ClosePrice",
"Volume",
"QuoteVolume"
]
res = requests.get(coin+day).json()
df = pd.DataFrame(res['result']['86400'], columns=df_columns)
df['CloseTime'] = df['CloseTime'].map(datetime.fromtimestamp)
df1= df.drop(columns=["OpenPrice","HighPrice","LowPrice","Volume","QuoteVolume"], axis=1)
df2=df['ClosePrice'].pct_change(1)
df3=df2*100
df4 = pd.merge(df1, df3, left_index=True, right_index=True)
df5 = df4.rename(columns={'ClosePrice_y': 'Rate of change'})
df6 = df5.rename(columns={'ClosePrice_x': 'ClosePrice'})
print(df6)・取引所のデータ取得についてはcryptowatchが非常に便利だった。
過去の価格変動の取得程度であるならば、個別の取引所でAPIの登録をする必要はなく、変数coinに格納されているアドレスを修正することで任意の取引所と通貨ペアの情報を入手できる。以下のサイトを参考にした。
・取得したデータを確認後、日付と終値のみのデータフレームに加工。更に日足の終値をもとに以下のコードから価格の変動率を作成した。
df['ClosePrice'].pct_change(1)・さらに分析における再現性をとるためシードの固定をおこなった。
TensorFlowに加えて、NumPy、Pythonの組み込み関数のシードの固定を以下のサイトを参考に実装した。
②価格と変動率の推移をグラフ化
円建ての価格推移と日足の価格変動率を表示させてグラフの性質を見てみる。価格推移のグラフでは2021年中頃から、大幅な上昇をしているが、これが学習において問題となる。時系列解析では時系列全体における前半70%を訓練データとして学習させ、後半30%の検証データで予測精度の算出と各種パラメータの調整を行うのが通例である。しかし、前半と後半で価格の乖離が激しすぎるため、パラメータの調整が困難となる。一方、変動率のグラフでは前半、後半での明確な乖離が発生していない。従って、変動率を用いた学習と分析を行うことにした。


③時系列解析における入力データの設定
時系列解析において、入力データと正解ラベルを作成する際、lookbackの数値指定が必要となる。これは正解ラベルを予測するために何日分のデータを使用するかを意味する。例えばlookback=3を指定した場合、過去3日分の変動率とその翌日の変動率が紐付くことになる。今回はバランスと実用性を兼ねて、7日分のデータからその翌日の変動率を予測する設定とした。
look_back = 7
train_X, train_Y = create_dataset(train, look_back)
test_X, test_Y = create_dataset(test, look_back)
④変動率のラベリング
今回は変動率の実値を予測する回帰ではなく、変動率を指定の段階毎にラベリングして、各予測データがどのラベルに該当するかという分類問題にした。パターンを絞ることで、予測精度を算出しやすく、トレードの実用性も期待できるからだ。 とりあえずラベルを以下の6パターンとした(xは変動率)。
#x>=10の場合5,x>=5の場合4,x>=0の場合3,x>=-5の場合2,x>=-10の場合1,x<-10の場合0に各値を置換
def labeling(x):
if x >= 10:
return 5
elif x >= 5:
return 4
elif x >= 0:
return 3
elif x >= -5:
return 2
elif x >= -10:
return 1
elif x < -10:
return 0
else:
return -1
#クラスラベル数
classlabel=6
train_Y=np.array(list(map(labeling, train_Y)))
test_Y=np.array(list(map(labeling, test_Y)))⑤予測モデルを構築し、予測精度を計測
まずは以下の通り予測モデルを暫定的な設定で構築し、数値を計測してみる。正解ラベルと予測データをそれぞれ分類モデルに対応させるための加工を行っている。
#(ラベルの数,lookbackの値)→(ラベルの数,lookbackの値,1)の3次元へ変更
train_X = train_X.reshape(train_X.shape[0], train_X.shape[1], 1)
test_X = test_X.reshape(test_X.shape[0], test_X.shape[1], 1)
#6パターンに分けた正解ラベルの数値を(0,0,0,0,0,0)の形状(数値は0~1)に分類
#one-hot ベクトルに対応させることが目的
train_Y2 = to_categorical(train_Y,classlabel)
test_Y2 = to_categorical(test_Y,classlabel)
# LSTMモデルの作成と訓練
model = keras.Sequential()
model.add(layers.LSTM(256, input_shape=(look_back, 1), return_sequences=True))
model.add(Dropout(rate=0.2))
model.add(layers.LSTM(128))
model.add(Dropout(rate=0.2))
model.add(layers.Dense(8))
model.add(Dropout(rate=0.2))
model.add(layers.Dense(classlabel))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', metrics=["acc"],optimizer="adam")
history = model.fit(train_X, train_Y2,validation_data=(test_X,test_Y2) ,epochs=10, batch_size=60, verbose=2)
# 予測データの作成
train_predict = model.predict(train_X)
test_predict = model.predict(test_X)
#argmax関数により、インデックス毎の最大の確率表記をとるカラム数を返すことで、正解ラベルとの照合を可能にさせる
DF_train_predict=pd.DataFrame(train_predict.argmax(axis=1))
DF_test_predict=pd.DataFrame(test_predict.argmax(axis=1))
#検証データの正解ラベルを表示(確認しやすいようにdfからndに修正)
Ndarray_test_predict=np.array(DF_test_predict).reshape(DF_test_predict.shape[0])
print(Ndarray_test_predict)
# 変数confmatに混同行列を格納
confmat = confusion_matrix(test_Y, Ndarray_test_predict)
print("混同行列")
print (confmat)
print("適合率/精度(Aと予測したうち実際にAである割合)")
print("Precision: {:.3f}".format(precision_score(test_Y, Ndarray_test_predict,average="weighted")))
print("Precision: ",precision_score(test_Y, Ndarray_test_predict,average=None))
print("再現率(結果がAであるうちAであると予測された割合)")
print("Recall: {:.3f}".format(recall_score(test_Y, Ndarray_test_predict,average="weighted")))
print("Recall: ",recall_score(test_Y, Ndarray_test_predict,average=None))
print("F値(適合率と再現率の調和平均)")
print("F1: {:.3f}".format(f1_score(test_Y, Ndarray_test_predict,average="weighted")))
print("F1: ",f1_score(test_Y, Ndarray_test_predict,average=None))一通り、プログラムを組み終えたので、とりあえず予測結果を出力してみる。今回は6パターンの多項混同行列になるが…

あれ?
出力した混同行列を確認したところ、なんとこのAI、クラスラベル2と3、つまり変動率-5%から5%までの範囲しか、予測値を算出してくれない。
原因を考えるため、訓練データと検証データそれぞれの変動率のヒストグラムを表示させてみる。

グラフでは-5%から5%までの範囲の変動率が大部分を占める一方で、10パーセントレベルの変動は殆ど発生していない(日足単位での変動率なので言われてみれば当たり前だが)。つまりAIは、学習を経て滅多に当たらない10%台を予測してみるより0%近辺の予測に徹した方が、予測精度を上げられると判断したのだ。これではいくら予測精度を上げても意味がない。
⑥クラス数の調整とクラス毎の重み付け
上述の通りサンプルデータの偏りがあるため、クラス数の調整とクラス毎の重み付けを行った。
・クラス数の調整
変動率のクラス数を6から3パターンに修正した。日足10%以上の変動は滅多に発生しないため、予測が難しい。また、3%以上の変動でも日足の変動率としては十分大きいため、わざわざ10%以上と区切って予測する意義がさほどないからである。クラス数を奇数に変更したのは、0%付近の値が僅かなプラスマイナスの誤差で異なるクラスに振り分けられ予測精度に影響を与えるためである。以下の通り、変動率3%を基準として分類し直した。
def labeling2(x):
if x >= 3:
return 2
elif x<3 and x >= -3:
return 1
elif x < -3:
return 0
else:
return -1
#クラスラベル数
classlabel=3・クラス毎の重み付け
fit関数の パラメータclass_weightに辞書型の数式(キーは各クラス)を代入することで、入力サンプル数が少ないクラスの損失値を増やすことができる。
class_weight のパラメータはスタンダードな設定である balanced を指定した。公式によると、balancedは以下の演算が行われるとのこと。
n_samples / (n_classes * np.bincount(y))
全体の要素数をクラス数とクラス毎の要素数で割ったものを各クラスごとの重みとする。
class_weight_sk=class_weight.compute_class_weight("balanced",classes=np.unique(train_Y),y=train_Y)
dict_class_weight_sk=dict(enumerate(class_weight_sk))
history = model.fit(train_X, train_Y2,validation_data=(test_X,test_Y2) ,epochs=18, batch_size=60, verbose=2,class_weight=dict_class_weight_sk)・出力して確認してみる
上記二点の修正反映してepoch数のみ最適化して出力してみたところ、混同行列の中央集中の解消が以下の通り確認できる。
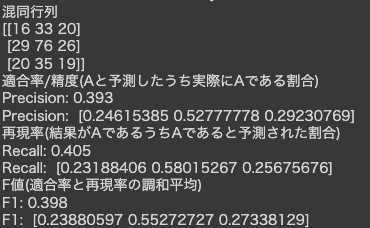
ただし、まだ中央値であるクラスラベル1と比較してクラスラベル0と2の予測精度が低いため、レイヤー層とパラメータの再調整を試みる。
⑦レイヤー層と各パラメータの調整
・LSTMモデルのユニット数の見直し
まずLSTMモデルのユニット数が適正なのかを検証した。
今回は以下の3パターンで検証した。なお、epoch数については、乱数によって変動が生じるため、乱数seed計10パターンの最適なepoch数の平均値を使用した。
A.ユニット数(256,128)の組み合わせ
B.ユニット数(64,32)の組み合わせ
C.ユニット数(8,4)の組み合わせ
A.ユニット数(256,128)の組み合わせ(epoch数=7)

B.ユニット数(64,32)の組み合わせ(epoch数=14)

C.ユニット数(8,4)の組み合わせ(epoch数=40)

このように3パターンで検証したが明確に優れている組み合わせを判別することは出来なかった。但しクラス単位での精度を見てみると、Aではクラス0の再現率が、Cではクラス2の再現率が極端に低い値となったことが分かる。このためバランスのとれたB(64,32)の組み合わせを使用することにした。
・通常の全結合ニューラルネットワークレイヤーの追加
上記の検証では導入していなかった全結合レイヤーを追加してepoch数14で出力してみる。
model = keras.Sequential()
model.add(layers.LSTM(64, input_shape=(look_back, 1), return_sequences=True))
model.add(Dropout(rate=0.2))
model.add(layers.LSTM(32))
model.add(Dropout(rate=0.2))
model.add(layers.Dense(8))
model.add(Dropout(rate=0.2))
model.add(layers.Dense(classlabel))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', metrics=["acc"],optimizer="adam")

全体的に予測精度が向上していることがわかる。他にもDropoutのレイヤーを消したり、逆にDropoutのレートを上げる等を試してみたが、明確な改善は見られなかったため、調整はここまでとした。
⑧乱数seedを変更して確認
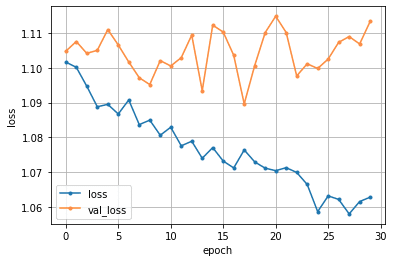
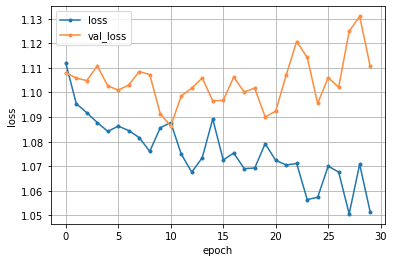
乱数によって予測精度が大幅に変わらないか確認をした。⑦でのseedは0であるが、seed1~5までをepoch数を14に固定して、予測結果と損失関数の推移を見てみる。
seed=1

seed=2


seed=3

seed=4


seed=5


確認してみると、乱数によって最適なepoch数は変動し、それによって予測精度に差が出ていることが分かる。但し上記のseed5パターンの平均は14であるため、epoch数の設定は14が最良ではあるようだ。
⑨まとめ
今回の検証に関しては残念ながら実用に足る十分なパラメータの組合せを見つけ出すことができなかった。仮想通貨はボラタリティが高く、特に大暴落はテクニカルではなく、ファンダメンタル的な要因で引き起こされることが多いため、判断材料が不足していた可能性がある。このためパラメータの調整だけでなく、相関性の高い新たな指標を見つけ出して組み込むことが課題と考える。とはいえ今回のモデルは株価にも流用できるため、逆にこのモデルで高い予測精度を出せる銘柄を探すアプローチも試してみる価値はある。最後に、作成したコード全体を掲載する。
from datetime import datetime
import requests
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import math
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, confusion_matrix, precision_score, recall_score, f1_score
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.layers import Dense, Dropout, Flatten, Activation
from tensorflow.keras.layers import Conv2D, MaxPooling2D
from tensorflow.keras.models import Sequential, load_model
from tensorflow.keras.utils import to_categorical, plot_model
from tensorflow.keras import optimizers
from sklearn.utils import class_weight
import tensorflow as tf
import numpy as np
import random
import os
# 乱数seed固定
def set_seed(seed=200):
tf.random.set_seed(seed)
# optional
# for numpy.random
np.random.seed(seed)
# for built-in random
random.seed(seed)
# for hash seed
os.environ["PYTHONHASHSEED"] = str(seed)
set_seed(0)
coin = "https://api.cryptowat.ch/markets/bitflyer/ethjpy/ohlc"
# periods・・・指定した秒足のデータを取得 ※日足は86400 週足は604800
day = "?periods=86400&after=0000000000"
df_columns = [
"CloseTime",
"OpenPrice",
"HighPrice",
"LowPrice",
"ClosePrice",
"Volume",
"QuoteVolume"
]
res = requests.get(coin+day).json()
df = pd.DataFrame(res['result']['86400'], columns=df_columns)
df['CloseTime'] = df['CloseTime'].map(datetime.fromtimestamp)
df1= df.drop(columns=["OpenPrice","HighPrice","LowPrice","Volume","QuoteVolume"], axis=1)
df2=df['ClosePrice'].pct_change(1)
df3=df2*100
df4 = pd.merge(df1, df3, left_index=True, right_index=True)
df5 = df4.rename(columns={'ClosePrice_y': 'Rate of change'})
df6 = df5.rename(columns={'ClosePrice_x': 'ClosePrice'})
print(df6)
print(type(df6.plot(x='CloseTime',y='ClosePrice',color="g")))
print(type(df6.plot(x='CloseTime',y='Rate of change',color="r")))
dataset = df6.drop(index=[0],columns=["CloseTime","ClosePrice"], axis=1)
dataset = dataset.astype('float32')
dataset=dataset.iloc[0:].values
# `dataset`を訓練データ、検証データに分割
train_size = int(len(dataset) * 0.67)
train= dataset[0:train_size]
test= dataset[train_size:len(dataset)]
# 入力データ・正解ラベルを作成する関数を定義
def create_dataset(dataset, look_back):
data_X, data_Y = [], []
for i in range(look_back, len(dataset)):
data_X.append(dataset[i-look_back:i])
data_Y.append(dataset[i])
return np.array(data_X), np.array(data_Y)
# 入力データと正解ラベルを作成(lookbackの数値は正解ラベルを予測するために何日分のデータを使用するかを意味する)
look_back = 7
train_X, train_Y = create_dataset(train, look_back)
test_X, test_Y = create_dataset(test, look_back)
#増減率のヒストグラムを作成する
fig=plt.figure()
ax1=fig.add_subplot(1,2,1)
ax2=fig.add_subplot(1,2,2)
ax1.set_title("TrainData")
ax2.set_title("TestData")
ax1.hist(train_Y, bins="auto")
ax2.hist(test_Y, bins="auto")
plt.xlabel("Rate of change")
plt.show()
def labeling(x):
if x >= 3:
return 2
elif x<3 and x >= -3:
return 1
elif x < -3:
return 0
else:
return -1
#クラスラベル数
classlabel=3
train_Y=np.array(list(map(labeling, train_Y)))
test_Y=np.array(list(map(labeling, test_Y)))
#(ラベルの数,lookbackの値)→(ラベルの数,lookbackの値,1)の3次元へ変更
train_X = train_X.reshape(train_X.shape[0], train_X.shape[1], 1)
test_X = test_X.reshape(test_X.shape[0], test_X.shape[1], 1)
#6パターンに分けた正解ラベルの数値を(0,0,0,0,0,0)の形状(数値は0~1)に分類
#one-hot ベクトルに対応させることが目的
train_Y2 = to_categorical(train_Y,classlabel)
test_Y2 = to_categorical(test_Y,classlabel)
# LSTMモデルの作成と訓練
model = keras.Sequential()
model.add(layers.LSTM(64, input_shape=(look_back, 1), return_sequences=True))
model.add(Dropout(rate=0.2))
model.add(layers.LSTM(32))
model.add(Dropout(rate=0.2))
model.add(layers.Dense(8))
model.add(Dropout(rate=0.2))
model.add(layers.Dense(classlabel))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', metrics=["acc"],optimizer="adam")
# クラス毎の重み付け
class_weight_sk=class_weight.compute_class_weight("balanced",classes=np.unique(train_Y),y=train_Y)
dict_class_weight_sk=dict(enumerate(class_weight_sk))
history = model.fit(train_X, train_Y2,validation_data=(test_X,test_Y2) ,epochs=14, batch_size=60, verbose=2,class_weight=dict_class_weight_sk)
# 予測データの作成
train_predict = model.predict(train_X)
test_predict = model.predict(test_X)
#argmax関数により、インデックス毎の最大の確率表記をとるカラム数を返すことで、正解ラベルとの照合を可能にさせる
DF_train_predict=pd.DataFrame(train_predict.argmax(axis=1))
DF_test_predict=pd.DataFrame(test_predict.argmax(axis=1))
#検証データの正解ラベルを表示(確認しやすいようにdfからndに修正)
Ndarray_test_predict=np.array(DF_test_predict).reshape(DF_test_predict.shape[0])
print(Ndarray_test_predict)
# 変数confmatに混同行列を格納
confmat = confusion_matrix(test_Y, Ndarray_test_predict)
print("混同行列")
print (confmat)
print("適合率/精度(Aと予測したうち実際にAである割合)")
print("Precision: {:.3f}".format(precision_score(test_Y, Ndarray_test_predict,average="weighted")))
print("Precision: ",precision_score(test_Y, Ndarray_test_predict,average=None))
print("再現率(結果がAであるうちAであると予測された割合)")
print("Recall: {:.3f}".format(recall_score(test_Y, Ndarray_test_predict,average="weighted")))
print("Recall: ",recall_score(test_Y, Ndarray_test_predict,average=None))
print("F値(適合率と再現率の調和平均)")
print("F1: {:.3f}".format(f1_score(test_Y, Ndarray_test_predict,average="weighted")))
print("F1: ",f1_score(test_Y, Ndarray_test_predict,average=None))
loss=history.history['loss']
val_loss=history.history['val_loss']
epochs=len(loss)
plt.plot(range(epochs), loss, marker = '.', label = 'loss')
plt.plot(range(epochs), val_loss, marker = '.', label = 'val_loss')
plt.legend(loc = 'best')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()