コリオリ力とは？~気象予報士を目指す~

2024年7月20日 22:55

気象予報士を目指す上で必ず理解しなければならない”コリオリ力”。
しかし、コリオリ力は見かけの力の一種である上に、私たちの日常生活にでは感じることのできない力のため、理解に苦しんでいる方も多いのではないでしょうか？
本説では、コリオリ力のイメージと数式を紐付けながら完全理解を目指します！

コリオリ力とは？　イメージから

コリオリ力とは、「回転する座標系で物体に作用する慣性力もしくは見かけの力」です。
もう少しわかりやすく言うと、

具体的なイメージを持って理解していきましょう。
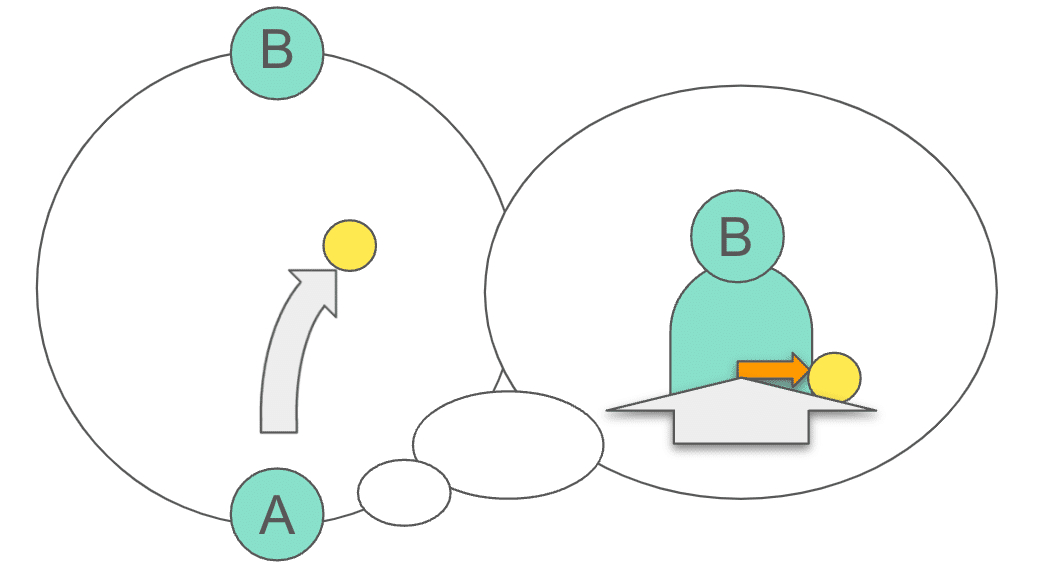
まずは、AさんがBさんに向かってボール（物体）を投げる場面を考えてみましょう（図１）。
もし、AさんとBさんとボールの存在する場所が回転していなければ、Aさんの想像するようにBさんにまっすぐ飛んで行くでしょう。

続いて、AさんとBさんの中心を軸に反時計回りに回転している地面が存在しており、その場所でAさんがBさんへボールを投げている場面を考えてみましょう(図２）。

そうすると、AさんがBさんへ投げた瞬間から、AさんとBさんは地面が回転しているために反時計回りに移動します（図３）。
しかし、空中に浮いているボールはそのまま真っ直ぐ進み、現在のBさんの位置から右にずれた場所に到達しようとします。

これを、Aさんの目線で見てみるとボールに右向きの力が働いて、ボールがBさんに向かって投げたはずなのにBさんの右側に着いてしまうように見えます（図４）。この右向きにかかっているように見える力を「コリオリ力」と呼びます。

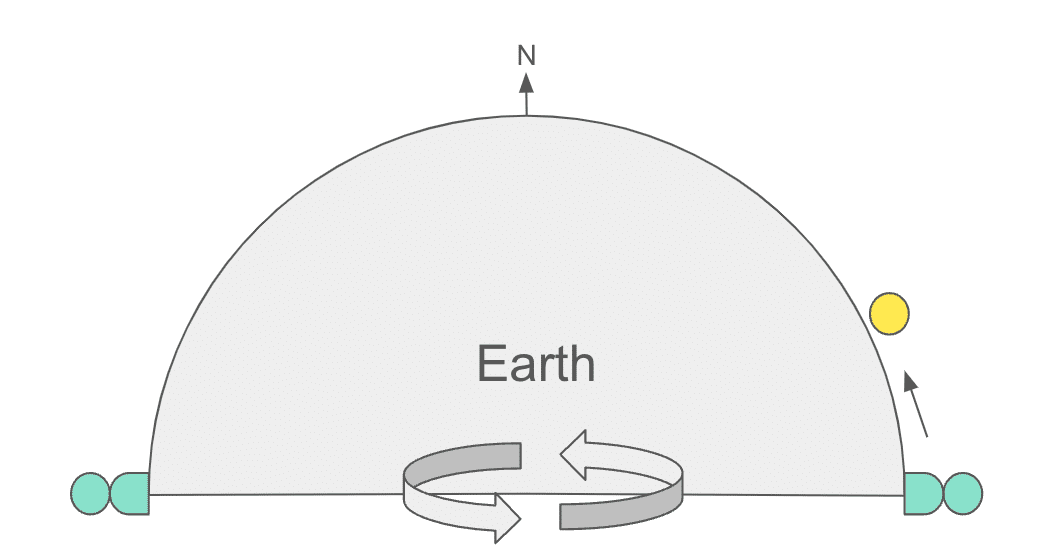
このコリオリ力は、自転する地球上の運動でも同様にかかります（図５）。
すなわち風や海流といった自然現象にもかかるため、気象学を学ぶ上で必須の力である、ということなのです。

ちなみに、日常生活で感じるほど大きな力では無いため、キャッチボールをしたところで球は右に曲がったりしません。
どれくらい小さいものかは、後述の導出編で触れたいと思います。

ちなみにこのコリオリ力は、小さな力とはいえ地球上のすべての物体に掛かっているのは確かなため、振り子のように外力が掛からずに動き続ける物体を見ていると軌道がわずかずつズレていきます。
これを観察するために用いられたのがフーコーの振り子になります。
国立科学博物館のB1Fに現役で飾られているので機会のある方は見てみましょう。

コリオリ力の式

ここでは、気象学・地球物理学全般で用いる地球の自転を起因とするコリオリ力について、その導出された式と使い方について学びます！
導出については、別記事で紹介しますので一旦この記事では数式の意味とコリオリ力を考えるタイミングを押さえておきましょう！

コリオリ力の大きさと作用する向き

$$
F（緯度\phiの地点での水平方向のコリオリの力）= 2m \Omega Vsin\phi
$$

$$
m=（物体の質量）, \Omega=（地球自転の角速度）　
\\\phi = （緯度）, V=（物体の水平速度）
$$

で力の向きは物体（流体）の進む方向に直角で、北半球なら流体の進む方向に対して右側、南半球なら物体（流体）の進む方向に対して左側を向きます。

ちなみにコリオリ力の物体由来ではない物理量（質量と速度以外）をコリオリパラメータと呼ぶ。

$$
コリオリパラメータ　 f = 2 \Omega sin\phi
$$

コリオリ力の大きさってどれくらい？

例えば、北緯30度を東向きに時速288km(秒速80m)で走る新幹線に乗っている体重50kgの人にかかるコリオリ力を考えてみましょう。
地球自転の角速度を$${\Omega}$$とすると、地球自転は１日(86400秒)で一周するため、

$$
\Omega= 2 \pi / 86400sec　= 7.292 \times 10^{-5} s^{-1}
$$

になります。
よって、コリオリ力Fは以下になります。

$$
\begin{align}
&F =2\times 50 \times80 \times 7.292 \times 10^{-5}\times sin(\pi/6)\notag\\
& \fallingdotseq 0.29 [N]\notag　　　　　
\end{align}
$$

以上から、新幹線に乗っている人には南向きに約30gの力が掛かっている。
日常生活では、摩擦力や人間の作る加速度の方が大きいため、ほぼ無視できる小ささであることがわかります。

コリオリ力を考えなければいけない時とは？

ここまでの話でコリオリ力の大きさは小さいため、あまり考えなくても良い力なのでは？と感じた方もいるかもしれません。
しかし、気象学ではこのコリオリ力の影響をよく考えなければいけない場合があります。

では、小さな力を考慮しなければいけない運動とは何でしょうか？
それは、大きく分けて２通りに分かれます。

速度が小さい場合
運動がゆっくり行われているため小さな力の影響で生じた運動の変化が観測できる、影響を考えなければいけない、ということ
運動の規模が大きい場合
運動の規模が大きいため小さな力の影響で生じた運動の変化でも観測できる、影響を考えなければいけない、ということ

便利なことに、この２通りのパターンについて、コリオリ力を考えなければならない条件をまとめた数があります。それがロスビー数です。

コリオリ力の影響度合い：ロスビー数

ロスビー数とは、コリオリ力による効果の重要度を表す指標で、コリオリ力と慣性力(加速度)の比を表す無次元数になります。

ロスビー数の定義は以下になります。

$$
\begin{align}
& R_0=U/fL \notag　\\
& ただし\notag \\
& f = 2 \Omega sin\phi \notag　 \\
&\Omega= 2 \pi / 86400sec　= 7.292 \times 10^{-5} s^{-1} \notag \\
&U=(速度スケール), L=(空間スケール),\notag　 \\
& f=（コリオリパラメータ）, \phi = (緯度) \notag　　
\end{align}
$$

速度スケールと空間スケールとは、だいたいの速度と現象の規模のことです。（地球現象では速度が常に一定ということはないため。）

そして、ロスビー数は以下のようにコリオリ力を考慮すべきか教えてくれます。

$$
\begin{align}
&R_0 \ll 1：コリオリ力について考慮しなければならない\notag\\
&R_0\gg 1：コリオリ力を無視して良い\notag
\end{align}
$$

気象学だと、主に総監規模（数千kmスケール）の現象でよく考慮しなければならない。

まとめ

コリオリ力とは、地球が自転しているために生じる見かけの力。
質量m・速度Vの物体にかかる大きさは、$${ 2m \Omega Vsin\phi}$$で、北半球なら進行方向右向き、南半球なら進行方向左向きにかかる。

気象学では主に大規模な現象で考えなければならない。