実験計画法 ～大きいサラダ菜を育てたいけど品種・肥料・日照時間・温度はどう調節すればいい？～

1. はじめに

こんにちは、LiNKX株式会社でAIエンジニアをしております伊藤といいます。

開発や研究の様々な現場では、製品の性能を改善するために、「その性能に関わる要因を実験によって調べ、良い値に設定する」という作業が定番です。

たいていの場合、要因の候補は何個も考えられます。担当者は、限られた時間の中で実験を繰り返し行い、要因を探っていかなくてはなりません。どう実験をするか、どう解析するか、それが問題です。

今回紹介する実験計画法とは、まさにこのような状況において

１．実験計画の立案

２．実験で取得したデータの解析方法

を教えてくれる手法です。

本ブログでは、まず、実験計画法を知らずに私がやっていた方法で、この最適化の問題にチャレンジします。そして、そこで何が問題になるかを明らかにします。最後に、実験計画法のやり方を説明します。

この記事は、以下のような方を対象として書きました。

＋解析を自分でやろうと考えている人

＋実験計画法がどんなものかをしっかり押さえておきたい人

2. 問題設定　大きいサラダ菜を育てたい

「大きいサラダ菜を育てたい。品種・肥料、その他もろもろの要因はどう選ぶのがよいのか」。

サラダ菜だけでなく、このような「要因探し」は様々な現場で必要とされています。車の燃費、ジャガイモの大きさ、薬の効き目、など、更には、刺身の鮮度、映画館の集客、などでも要因が分かるととてもハッピーです。

機械学習をする方だったら、モデルのハイパーパラメータの調節を時間かけてやったりしますが、これも同じ要因探しの問題として当てはまります。私はこの場合が多いです。

ここでは、具体的な例として、サラダ菜を大きく育てるための要因を考えてみます。

　要因の候補としては、例えば、品種、肥料、日照時間、温度、湿度、水の種類、などがありそうです。一方、要因には関係のない個体間のバラツキも存在することも意識しておきましょう。

要因には、まだまだ候補がありそうですが、ここでは、初めの４つの、品種、肥料、日照時間、温度に着目していきましょう。このように要因の中から分析の対象としたものを因子(Factor)と呼びます。

各因子には、それぞれが「とる値」があります。

例えば、

品種は、「緑サラダ菜」か「赤サラダ菜」

肥料は、「化学肥料」か「有機肥料」

日照時間は、「短い（6時間）」か「長い（12時間）」

温度は、「低い（18℃）」か「高い（25℃）」

のような値です。

このように各因子が「とる値」を、その因子の水準(Level)と呼びます。そして、この例のように、「とる値の種類」が2つの場合を2水準といいます。実際には、3水準や4水準で考えたいときもあります。そして、水準が多い場合の解析も可能です。しかし、ここでは最も単純な2水準で考えていきます。

サラダ菜の例での因子と水準をまとめると、以下のようになります。

表１

では、ここから先は問題を抽象化して、品種、肥料、日照時間、温度の因子を、単純に、A、B、C、Dと表し、それらの水準をA1/A2、B1/B2、C1/C2、D1/D2のように表していきます。

そして、サラダ菜の大きさをスコア（score）と呼ぶことにしましょう。

解くべき問題は、

「スコアが大きくなる各因子の水準を見つけること。」

となります。

3. 普通の方法で良い水準を探す

それでは、まずは、実験計画法を知る前に私が普通にやっていた方法で、サラダ菜の水準探しをしてみます。

まず、因子Aに着目し、A1とA2を比較することを考えます。他の因子は、B1、C1、D1に水準を揃えます。表２の2回の実験を行い、「score」（結果）を比較します。

表２

この実験では、A2よりもA1の時の方がscoreが高かったので、A1の方が良いことが分かりました。

次は、因子Bに着目しB1とB2を比較します。Aの因子は先ほど良かったA1に固定し、CとDはこれまでと同じC1、D1に固定します。表３の上段はすでに行った実験なので、下段の実験のみを追加します。

表３

すると、更に大きいscore、12が出ました。BはB2の方が良いことが分かりました。

次は、因子Cに着目して実験です。AはA1に、BはB2に固定します。Dはこれまで通りのD1に固定します。4回目の実験だけ新規に行い、scoreを出します。

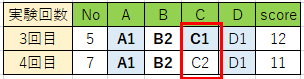
表４

因子Cに対しては、C1の方がscoreが1だけ多かったことから、C1が良いとしました。

最後は因子Dです。同様な考え方で、A、B、Cの因子はそれぞれ、A1、B2、C1に固定して、Dだけ変えて比較します。5回目の実験をしてscoreを出します。

表５

結果、D2よりもD1のscoreが良いのでD1が良いことが分かりました。

以上で実験は終了です。たった5回の実験で結論が導かれました。

まとめますと、A、B、C、D、の水準は、それぞれ、A1、B2、C1、D1が良いということになりました。サラダ菜に戻ると、

普通法「赤サラダ菜（A1）で有機肥料（ B2）を使い、日照時間は短く（C1）、温度は低い（D1）」がよい。

という結論になります。

この普通法（名前がないと不便なので、このように命名しておきます）で、まったく問題ないと思えるのですが、実は、間違った結論が導かれてしまっているのです。

4．データの種明かし

今考えたデータは、実は人工データでした。それをどう作ったかを説明します。

4因子に対してそれぞれが2水準あるので、全ての組み合わせは、

2 x 2 x 2 x 2 = 16通り

です。人工データでは、そのそれぞれに対して表６のようにscoreを決めていました。

表６

普通法では、この16通りの中から、5回の実験を選んで実行し、5回目の実験No5がベストという結論を導いたことになります（表６、左の実験回数の列）。

しかし、実は、この表６で一番scoreが多かったのはNo13でした。No13～16は、全て普通法のベストを上回っています。これを見ると、残念ながら普通法は失敗だったと言わざるを得ません。

「scoreがでたらめに割り振られていたのではないか？」と思われるかもしれませんので、そうではないことを説明します。

下の表７は、データのレシピです。base、A、B、AxB、noise の列ごとの数値の和をとってscoreを決定しています。例えば、No1のデータは、11-1-5+3+1 = 9 となるので、score=9  と決まります。

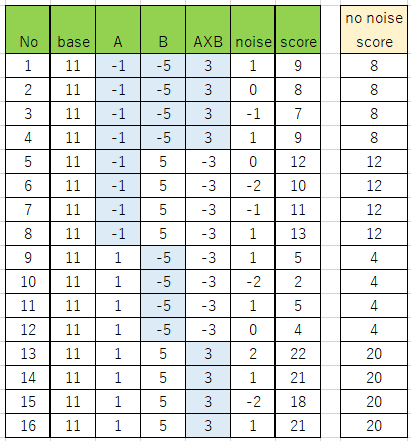
表７

表の意味を説明します。まず、baseの列についてです。これは、全てのNoに同等に与えるベース点数です。全てに11を与えています。

次に、Aの列です。これは、Aの効果（品種）です。A1（青のセル：緑サラダ菜）がある行には-1を加え、A2（白のセル：赤サラダ菜）があるものには+1を加えます。±1なので、Aの効果は小さめです。

次に、Bの列です。Bの効果（肥料）を加えます。B1（青のセル：化学）がある行には-5を加え、B2（白のセル：有機）がある行には+5を加えます。±5なので、Bの効果は大きめです。

次に、AxBと書いた列です。これは、AとBの交互作用という効果です。例えば、特定の肥料が特定の品種のみに有効、といった二つの因子が関係した効果に対応します。

（A1とB1）または（A2とB2）が割り振られている行（青いセル）には+3を加え、それ以外の行には-3を加えます。±3ですので、そこそこの大きさの効果です。サラダ菜の例でイメージすると、「緑サラダ菜は化学肥料が合っていて、赤サラダは有機肥料が合っている」という効果になります。

最後はnoise の列で、平均が0のノイズを加えます。これは因子に関係のないサラダ菜の個体差の違いを表しています。

＜少し数学的になりますが、ノイズについての補足説明です。ノイズは、平均が0で標準偏差σのガウス分布から独立に16個サンプルしたものです。和をとっても完全に0になるわけではありません。またここではノイズの値を整数に丸め込んでいます。σは任意ですが、すべてのノイズは同じσから生成されています。＞

C（日照時間）とD（温度）の要因は入れていません。つまり、普通法で見た、C1とC2の差、D1とD2の差は単にノイズ（個体差）から来るものだったと言えます。実際には、サラダ菜の成長が日照時間や温度に関係がないことはあり得ないかもしれませんが、ここではその差が無視できるほど小さかったと考えてください。

以上がデータの作り方でした。

それでは、結局のところ、どのNoの組み合わせが一番良いと言えるのでしょうか。scoreでみればNo13でしたが、No13には偶然+2という大きめのノイズが入っていた影響もあります。

そこで、左にノイズだけ入れていないscoreを右の列に出しました(no noise score)。これを見ると一目瞭然です。No13～16が最高で同じ値で20です。よって、表６と表７を照らし合わせれば、

「AはA2、BはB2、CとDはなんでもよい（関係ない）」

という結論が正解になります。サラダ菜の例に戻ると、

正解「赤サラダ菜（A2）で有機肥料（B2）を使う。日照時間と温度は関係ない。」

です。

一方、普通法の結論は以下のようなものでした。

普通法「緑サラダ菜（A1）で有機肥料（ B2）を使い、日照時間は短く（C1）、温度は低くする（D1）」

普通法が失敗してしまった原因はなんだったのでしょうか。

一つは、AとBの交互作用が入っていたせいでした。普通法は、交互作用があると間違った方向に結論が流される場合があるのです。サラダ菜の例だと、相性の良い「赤サラダ菜と有機肥料」の組み合わせが一度も試されることなく、結論が導かれてしまいました。

もう一つ、原因があります。普通法は1対1の比較をするので、検出した差が単にノイズのせいなのか、それとも、因子の水準の違いによるものなのかを区別できないのです。このことから、CとDはなんでもよいという結論は原理的に出せません。

うーん、残念、普通法。しかし、ここで普通法を完全否定はしたくありません（私もまだ使いたい）。

交互作用が考えにくく、ノイズレベルも低いことが分かっていれば、普通法は実験回数が少ないという利点もあるので、利用価値は十分にあるはずです。交互作用がなくノイズも十分に小さいデータなら普通法が正しく機能することは簡単に立証できるでしょう。普通法の使い方については、最後のまとめでも述べたいと思います。

5. 実験計画法

さて、前置きがだいぶ長くなりましたが、ここからがメインの実験計画法の解説になります。実験計画法を正しく使えば、「少ない実験回数」（普通法よりちょっと増えますが）で、「因子の効果とノイズの区別」も、「交互作用の検出」も、可能です。冒頭で述べましたように、実験計画法は以下の二つのパートからなります。順番に説明していきます。

１．実験計画の立案

２．実験で取得したデータの解析方法

実験計画の立案（直交表）

では、実験計画の立て方です。実験計画法では状況によって方法が提案されていますが、ここでは直交表という表を使って計画する方法を紹介します[1][2]。

まず、4因子2水準の実験に適した、L_8(2^7)（8は下付き、7は上付き）という種類の直交表を表８に示しました。L_8(2^7)表の「8」は行数、「7」は列数、「2」は水準数を表しています。直交表は色々なサイズのものが作られており、実験の因子数と水準数、また、注目したい交互作用の数などによって、適切な直交表を選びます。具体的な選び方は参考文献[1][2]を参照してください。

表８　L_8(2^7) 直交表 (8は下付き、7は上付き)

この表を使って実験する水準のパターンを決めるのですが、ここでは手順だけ説明します。まず、表８の列のどこかに、因子A、B、C、Dを割り当てます。ここでは、１、２、４、７列目に割り当てました（下の段）。

調べたい効果によって割り当て方を変えるのですが、ここでは、A, B, C, Dの因子の効果だけでなく、AxB、AxC、BxCの交互作用も調べられる割り当てを選びました。そのかわり、Dに関係した交互作用の検証はできません。

次に、表８にしたがって、実験を行う水準の組み合わせを決めます。

まず、No1の横の行で、ABCDを割り当てた数値のみを読むと、（１１１１）となっています。No２は（１１２２）です。これらの４つの数値を、ABCDの水準と解釈して、No1は（A1、B1、C1、D1）、No2は（A1、B1、C2、D2）とします。

これが実験すべき水準の最初の２つとなります。

同様な手続きで、No８まで置き換えをして表にしたものが、完成した実験計画になります（表９）。すべての組み合わせ16通りを試さなくても、8回の実験で十分ということになります（普通法の5回より多いが、交互作用とノイズとの区別が検出可能になっている）。なぜ、これで良いのか疑問に思うと思いますが、それは次の解析の方法で説明します。

表９

実験で取得したデータの解析方法（分散分析）

それでは、表９にしたがって実験を行いscoreを入れた表１０から、どの因子がscoreに影響を与えているか、交互作用はあるか、を調べていきます。

表１０

方法は、分散分析という統計手法です。手計算でもできますが、計算ミスを防ぐためにも、既存のツールを使った方がよいでしょう。しかし、分散分析をするまえに、なぜ、表１０のラインナップで良いのかを少し考えてみたいと思います。

因子Aに着目します。表１１を見てください。因子Aに対してA１の水準をセットしたものは上側の4回分、A２にセットしたものは下の4回分になります。この時のscoreの平均をA１とA２のグループで求めます。すると、A１の方は9.75、A1の方は12.5となります。つまり、因子AではA１よりもA２が良いと言えそうです。

表１１

しかし、この平均の計算でB、C、Dの影響はないと言えるのでしょうか。

B、C、Dの水準は実験によってバラバラですが、例えばDに着目すると、上のグループでD1、D2、D2、D1、下のグループでD2、D1、D1、D2と水準の種類と数が一致していることが分かります。同様のことが、BでもCでも言えます。

よって、平均してもBCDの影響は上と下のグループで同じであり、Aの平均の計算に影響は与えていないということになります。実に巧妙です。

また、Aの効果を計算するのに、4回ずつの実験を比較できるというところもポイントです（普通法では1回ずつを比べました）。このことで、Aの効果が本当なのか、または、単にノイズによる誤差なのかを、統計の考え方で区別することができるのです。

同様の計算が、B、C、Dでもできます。注目していない因子の水準(Level)は、いつも比較するグループ間で同じ水準が同数入るようになります。表１２に、各因子（Factor）の各水準における平均scoreをまとめました。数値が大きい水準のセルを黄色く色を付けています。

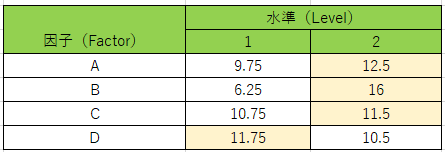
表１２

この計算は交互作用（Interaction）の検出にも使えます。AｘＢの交互作用の場合には、（A1とB1またはA2とB2）と、（A1とB2またはA2とB1）を比較するので、（直交表番号1 , 2, 7, 8）と（3, 4, 5, 6）を比較すればよいのですが、この場合でも、それ以外の因子の水準が同数ずつ入ります。すごい。

計算すると表１３のようになります。AとBは、A1とB1またはA2とB2、のときにscoreが高くなることが分かります。

表１３

では、いよいよ実際に表１０のデータを、分散分析にかけてみます。ここではpythonのライブラリーstatsmodels を使いました[3]。計算は一瞬で終わります。その結果を表１４にまとめました。

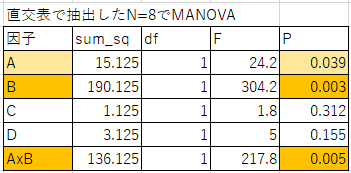
表１４

表１４の左の列が、調べた因子を表しています。ここでは、A,B,C,DとAxBに着目しています（AxB, BxCはこの計算では除外しています）。

右側の列のPが検定による有意性を表しています。この値が、0.05以下だったら、意味の有る差があるとして有意差ありと判定します。0.01以下だったら、より確実な有意差ありと判定します（sum_sq, df, F に関しては、計算過程で出てくる変量で、それぞれ「平方和」、「自由度」、「F値」といいます。ここでの説明は省略します。[1][2]を参考にしてください）。

AとB、そしてAxBのPが0.05よりも小さいので、因子AとBそして、AとBの交互作用に有意差が検出されていることが分かります。一方、CとDに有意さは認められませんでした。

「有意さが認められない」ことは、厳密には、「有意さがない」こととは別なので注意が必要ですが、この結果は、実際のデータに一致していると言えるでしょう。

表１３の結果は、要因となる因子を特定しているだけなので、どの水準がよいのかは分かりませんが、表１１と表１２と合わせて考えることで、

「AはA２、BはB２、CとDはscoreに関係があるとは言えない」

という結論を導くことができます。サラダ菜の例に戻ると、

実験計画法「赤サラダ菜（A2）で有機肥料（B2）を使う。

　　　　　　　　　日照時間と温度は重さに関係があるとは言えない。」

となります。正解と照らし合わせると、

正解「赤サラダ菜（A2）で有機肥料（B2）を使う。日照時間と温度は関係ない。」

となりますので、「関係があるとはいえない」と「関係がない」という言い回しの違い以外は、一致しました。統計学的に「関係がない」といいきるのはもともと難しいことなので、上記のような実験計画法の結論が現実的な解答としてベストとなります。

これで、実験計画法の紹介はおわりです。

直交表の実験計画、本当にエレガントですね。今回は、4因子2水準の例で説明しましたが、因子や水準の規模が大きくなればなるほど、実験計画法からのご利益は大きくなります。

お読みいただきありがとうございました。

ここでは、天下り的に手続きを説明しましたが、その理屈や色々な場合での使い分けなどは、参考文献の図書が参考になります。

6. まとめ

普通法

１つの因子の水準のみを変化させてscore を比較し、良い方の水準に固定する。同様に次の因子の水準を変化させて実験していく。この手続きですべての因子をベストの水準に固定する。実験回数は少ないが、交互作用がある場合に誤った結論に導かれる場合がある。また、因子からくる差とノイズからくる差の見分けがつかない。

しかし、一つの因子にのみ着目して手っ取り早く試すには有効と思われる（実験計画法はすべて実験をしないと結論がでない）。そして、同じ条件を2回か3回繰り返して比較すれば、因子による差とノイズによる差も区別可能。

実験計画法（直交表）

直交表に基づき実験する水準のパターンを決定する。分散分析によって、有意差のある因子、交互作用が検出できる（ノイズではないことを有意差として判定できる ）。因子の数が多ければ多いほど、直交表の威力は絶大になる。例えば、9因子（2水準）の効果は、わずか16回の実験で確認することができる[2]（すべての組み合わせを考えたら29=512）。

あえて欠点を述べるとすれば、計画を作るのにひと手間かかるということと、計画したすべての実験を終わらせないと結論がだせないという点だろうか。

7. 参考文献

[1] 永田靖、入門実験計画法、日科技連（図書）

大学の教科書のような本で、しっかりと体系立てて解説されています。数学的な根拠の解説もあります。とても良い本でした。

[2] 大村平、改訂版　実験計画と分散分析の話、日科技連（図書）

親しみのある口調で、具体的で直感的な分かりやすい解説をしてくれます。それでいて十分な範囲を網羅しています。とても良い本でした。人工データで解説する方法は、この本を参考にさせていただきました。

[3] statsmodels (python の統計計算ライブラリ）https://www.statsmodels.org/stable/index.html

分散分析に使いました。分散分析は２因子までならエクセルでも可能です。