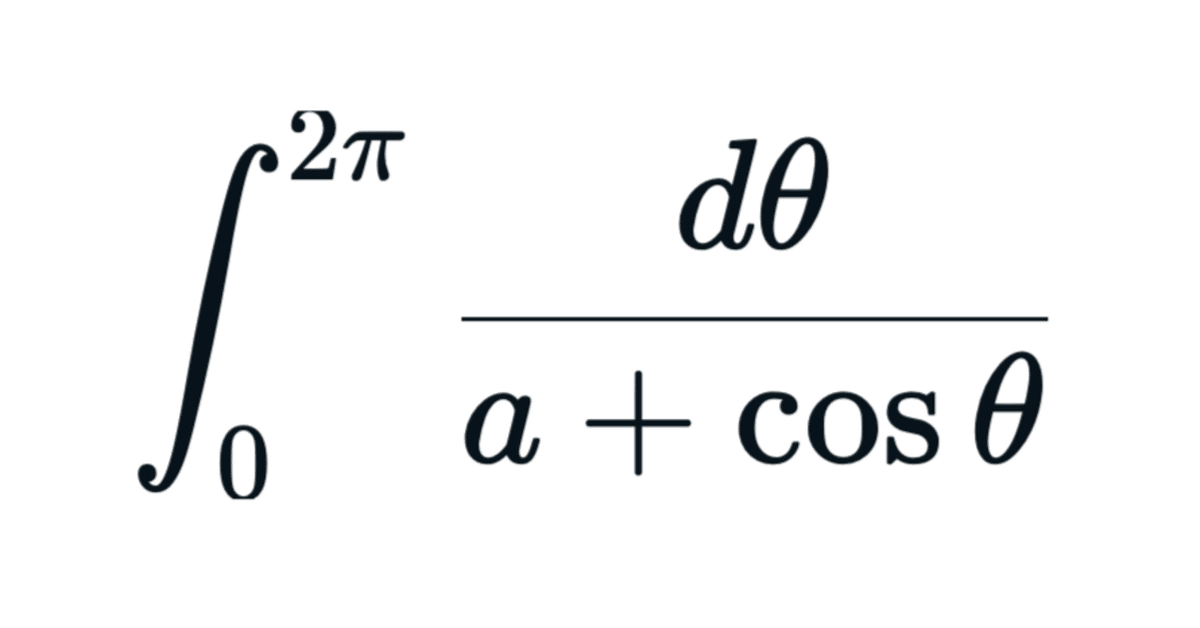
複素関数論を使って定積分の値を求める
この記事は上のアドベントカレンダーの10日目です。
はじめに
解析学の教科書によく載っている冒頭画像の定積分を求めてみます。
いろいろな方法があるようですが、本記事では複素関数論の知識を活用して計算してみます。
教科書にも載っているような解法ではあるのですが、複素関数論のちょっとした復習にはなると思います。
※本記事を読むには大学2年(3年?)の複素関数論の知識が必要です。
考えるべき積分
$${a>1}$$のとき、次の積分の値を求める問題を考えます。
$$
\int_{0}^{2\pi}\frac{d\theta}{a+\cos\theta}
$$
これは解析学の教科書にもよく載っている問題だと思います(多分)。
とりあえず留数定理による計算
$${z=e^{i\theta}=\cos\theta+i\sin\theta}$$と変数変換します。
$${z+z^{-1}=2\cos\theta}$$、$${dz=ie^{i\theta}d\theta=izd\theta}$$です。
$$
\begin{array}{|c||ccc|}\hline
\theta &0&\to&2\pi\\ \hline
z&e^{0}&\to&e^{2\pi i}\\ \hline
\end{array}
$$
上の表から、次のように実軸上の積分路を$${\mathbb{C}}$$上の単位円周に変更できます。
$$
\begin{align*}
&\int_{0}^{2\pi}\frac{d\theta}{a+\cos\theta}\\
=&\int_{|z|=1}\frac{1}{a+(z+1/z)/2}\frac{dz}{iz}\\
=&\frac{2}{i}\int_{|z|=1}\frac{dz}{2az+z^2+1}\\
\end{align*}
$$
※$${\int_{|z|=1}}$$は単位円周上を反時計回りに1周動く積分路を表すとします。
2次方程式$${z^2+2az+1=0}$$の解$${\alpha,\beta}$$は,
$$
\alpha=-a+\sqrt{a^2-1},\\
\beta=-a-\sqrt{a^2-1}
$$
であり、両方とも実数です。
解と係数の関係から$${\alpha+\beta=-2a,\ \alpha\beta=1}$$ですから、
$${\alpha,\beta}$$はともに実軸の負の部分にあります(ということは上の式をじっと見ても分かるのですが)。
さらに、$${\alpha}$$は単位円の中にあり、$${\beta}$$は単位円の外にあります($${\alpha, \beta}$$は互いに単位円に関して鏡像の関係にあるとか、円対称とか言ったりもします)。
よって、上の積分は次のように書くことができます。
$$
\begin{align*}
&\frac{2}{i}\int_{|z|=1}\frac{dz}{2az+z^2+1}
=\frac{2}{i}\int_{|z|=1}\frac{1}{(z-\alpha)(z-\beta)}dz
\end{align*}
$$

さくっと済ませるなら、留数定理を使って計算すればよいでしょう。
被積分関数の単位円内にある極は$${\alpha}$$のみで、それは1次の極ですから、その留数は、
$$
\mathrm{Res}(\alpha)
=\lim_{z\to\alpha}(z-\alpha)\frac{1}{(z-\alpha)(z-\beta)}
=\frac{1}{\alpha-\beta}
=\frac{1}{2\sqrt{a^2-1}}
$$
です。よって、問題の積分は次のように求められます。
$$
\begin{align*}
&\int_{0}^{2\pi}\frac{d\theta}{a+\cos\theta}
=\frac{2}{i}\cdot2\pi i\mathrm{Res}(\alpha)
=\frac{4\pi}{2\sqrt{a^2-1}}
=\frac{2\pi}{\sqrt{a^2-1}}
\end{align*}
$$
不定積分から考えてみる
上記で積分の値は求められましたが、その途中で次のように部分分数分解ができることに気づいたと思います。
$$
\begin{align*}
&\frac{2}{i}\int_{|z|=1}\frac{1}{(z-\alpha)(z-\beta)}dz\\
=&\frac{2}{i}\frac{1}{\alpha-\beta}\int_{|z|=1}\left(\frac{1}{z-\alpha}-\frac{1}{z-\beta}\right)dz
\end{align*}
$$
これを利用して、上の計算結果が正しいことを再確認してみましょう(というか、さっきも部分分数分解してから留数定理使えばよかったですね……)。
次のような不定積分ができます($${C}$$は積分定数)。
$$
\begin{align*}
&\int\left(\frac{1}{z-\alpha}-\frac{1}{z-\beta}\right)dz\\
=&\log(z-\alpha)-\log(z-\beta)+C\\
=&\log|z-\alpha|e^{i\arg(z-\alpha)}-\log|z-\beta|e^{i\arg(z-\beta)}+C\\
=&\log|z-\alpha|+i\arg(z-\alpha)-\log|z-\beta|-i\arg(z-\beta)+C
\end{align*}
$$
よって、積分路が極を回るのかどうかに気をつければ、積分路の始点と終点から定積分を計算できます。
積分路が単位円である場合、$${\log(z-\alpha)}$$の方は分岐点$${\alpha}$$の回りを1周することになりますから、偏角は$${2\pi}$$だけ増加します。
一方、$${\log(z-\beta)}$$の方は、単位円の中に分岐点はないため、始点から終点に動いても偏角は変わりません。ゆえに、$${\log}$$のbranchを適当にとって、
$$
\begin{align*}
&\int_{|z|=1}\left(\frac{1}{z-\alpha}-\frac{1}{z-\beta}\right)dz\\
=&\left[i\arg(z-\alpha)\right]_{\arg(z-\alpha)=\phi}^{\arg(z-\alpha)=\phi+2\pi}-\left[i\arg(z-\beta)\right]_{\arg(z-\beta)=\phi}^{\arg(z-\beta)=\phi}\\
=&(\phi+2\pi-\phi)-(\phi-\phi)\\
=&2\pi
\end{align*}
$$
と計算できます。したがって、
$$
\begin{align*}
&\int_{0}^{2\pi}\frac{d\theta}{a+\cos\theta}
=\frac{2}{i}\frac{1}{\alpha-\beta}2\pi
=\frac{4\pi}{2\sqrt{a^2-1}}
=\frac{2\pi}{\sqrt{a^2-1}}
\end{align*}
$$
となり、上記と同じ結果が得られます。
ここで行った偏角の変化を見る方法は、上記の留数定理と実質同じことをしているだけですが、不定積分の結果も得ているため、積分路がジョルダン閉曲線ではなくジョルダン曲線の場合にも適用できます。
一次分数変換を考える方法
上記の不定積分を見た際、次のようにできることに気づいたと思います。
$$
\begin{align*}
&\frac{2}{i}\int_{|z|=1}\frac{1}{(z-\alpha)(z-\beta)}dz\\
=&\frac{2}{i}\frac{1}{\alpha-\beta}\int_{|z|=1}\left(\frac{1}{z-\alpha}-\frac{1}{z-\beta}\right)dz\\
=&\frac{1}{i\sqrt{a^2-1}}\left[\log(z-\alpha)-\log(z-\beta)\right]_{|z|=1}\\
=&\frac{1}{i\sqrt{a^2-1}}\left[\log\frac{z-\alpha}{z-\beta}\right]_{|z|=1}
\end{align*}
$$
よって、単位円を1周するとき、被積分関数$${\log\dfrac{z-\alpha}{z-\beta}}$$は極を回るのかどうかを見てみます。
$${\alpha-\beta\neq0}$$であるため、$${\dfrac{z-\alpha}{z-\beta}}$$は、一次分数変換と呼ばれるものです。
$${w=f(z)=\dfrac{z-\alpha}{z-\beta}}$$とします。
一次分数変換では、円円対応が成り立ちます。すなわち、$${z}$$が単位円周上を動くとき、$${w}$$もある円上を動きます。実際、
$$
\begin{align*}
w&=\dfrac{z-\alpha}{z-\beta}\\
z&=\dfrac{-\beta w+\alpha}{-w+1}\\
|z|&=\left|\dfrac{-\beta w+\alpha}{-w+1}\right|=1\\
|-\beta w+\alpha|&=|-w+1|\\
(-\beta w+\alpha)(-\beta \overline{w}+\alpha)&=(-w+1)(-\overline{w}+1)\\
\beta^2|w|^2-\alpha\beta (w+\overline{w})+\alpha^2&=|w|^2-(w+\overline{w})+1\\
(\beta^2-1)|w|^2&=1-\alpha^2\\
|w|^2&=\frac{1-\alpha^2}{\beta^2-1}=\alpha^2\frac{1-\alpha^2}{\alpha^2\beta^2-\alpha^2}\\
&=\alpha^2\frac{1-\alpha^2}{1-\alpha^2}=\alpha^2
\end{align*}
$$
となり、$${w}$$は原点を中心とする半径$${|\alpha|}$$の円周上にあることが分かります。
では、$${z}$$が単位円周上を反時計回りに動くとき、$${w}$$は反時計回りと時計回りと、どちらで動くのでしょうか。
これは、$${z=1,i,-1,-i}$$に対する$${w=f(z)}$$の値を見ればよいです。
$$
\begin{align*}
f(1)&=\frac{1-\alpha}{1-\beta}
=\alpha\frac{1-\alpha}{\alpha-\alpha\beta}
=\alpha\frac{1-\alpha}{\alpha-1}
=-\alpha>0\\
f(i)&=\frac{i-\alpha}{i-\beta}
=\frac{(i-\alpha)(-i-\beta)}{1+\beta^2}
=\frac{1+\alpha\beta+i(\alpha-\beta)}{1+\beta^2}\ (\in上半平面)\\
f(-1)&=\frac{-1-\alpha}{-1-\beta}
=\alpha\frac{-1-\alpha}{-\alpha-\alpha\beta}
=\alpha\frac{-1-\alpha}{-\alpha-1}
=\alpha<0\\
f(-i)&=\frac{-i-\alpha}{-i-\beta}
=\frac{(-i-\alpha)(i-\beta)}{1+\beta^2}
=\frac{1+\alpha\beta-i(\alpha-\beta)}{1+\beta^2}\ (\in下半平面)
\end{align*}
$$
以上から、$${w}$$も反時計回りに動くことが分かります。
または、$${w=f(z)}$$は単位円内には、1次の零点$${z=\alpha}$$をもち、極を有しないため、偏角の原理から、次のような等式が成り立ちます。
$$
\begin{align*}
\frac{1}{2\pi i}\int_{|z|=1}\frac{w'}{w}dz&=1\\
\frac{1}{2\pi i}\int_{|w|=|\alpha|}\frac{dw}{w}&=1\\
\int_{|w|=|\alpha|}\frac{dw}{w}&=2\pi i
\end{align*}
$$
しれっと$${\int_{|w|=|\alpha|}}$$と書いていますが、$${w}$$はどっち回りに動くのかこの時点では分かっていなかったはずです。しかし、等式の右辺が$${2\pi i}$$であることから$${w}$$が反時計回りに1周回ることが分かります。もし時計回りなら、最後の積分の値は$${-2\pi i}$$となるはずです。
※ただし、これは「本来の積分の結果を求めるために、$${w}$$が動く向きを知ろうとして、別の積分の値を考えている、という回りくどいことをしてしまっています。
とにかく、これで、求めたかった積分は、
$$
\begin{align*}
&\frac{1}{i\sqrt{a^2-1}}\left[\log\frac{z-\alpha}{z-\beta}\right]_{|z|=1}\\
=&\frac{1}{i\sqrt{a^2-1}}\left[\log w\right]_{|w|=|\alpha|}\\
=&\frac{2\pi i}{i\sqrt{a^2-1}}\\
=&\frac{2\pi}{\sqrt{a^2-1}}
\end{align*}
$$
となり、やはり同じ値が得られました。
この方法も、不定積分を求めた時と同様に、積分路の始点と終点に応じて$${w}$$の値がどうなるか考えれば、積分路がジョルダン閉曲線でない場合にも使えそうです。
まとめ
定積分の値を、複素関数論の知識を利用して、3通りの方法で求めてみました。
実質的には、極の回りを回るのかどうかを考えているだけで、やっていることは同じです。ただし、不定積分の方法、一次分数変換の方法は、ジョルダン閉曲線以外の積分路にも活用できそうな汎用性があります。
積分の計算を通して複素関数論の復習になったと思います。
(おわり)
参考文献
堀川穎二『複素関数論の要諦[新装版]』2015年、日本評論社
※本記事の内容は、普通の複素関数論の教科書に載っていると思います。とりあえず上記の文献だけ挙げておきます。大学の講義のライブ感が伝わる好著だと思います。
