電気通信大学情報理工学域一般選抜前期日程サンプル問題【1】浮動小数点方式の表現を題材にした問題

和田　勉（長野大学）

解説する問題

　ここでは，電気通信大学から参考文献1）で令和6年（2024年）7月に公開された，情報理工学域一般選抜前期日程「情報」サンプル問題のうち，【1】の問題を解説します．同大学ではすでに令和5年（2023年）11月に「試作問題」が公開されていますが今回これに続いて公開されたものです．なお先に公開された「試作問題」のうち第3問は本シリーズですでに解説されています²⁾．

　今回は，浮動小数点方式を表す方式のひとつ，FP8と呼ばれる方式を題材にしたものです³⁾．

固定小数点方式と浮動小数点方式

　問題の解説に入る前に，この問題で題材としている浮動小数点方式を解説します．まず数値の二進法による表現として通常使われる固定小数点方式について触れ，そのあと浮動小数点方式の考え方を紹介します．

固定小数点方式

　「情報のデジタル化」で数値の二進法による表現を学ぶと，以下のような話が出てきます．

　たとえば符号ビットおよび値（絶対値）7ビット，計8ビットで表した例を示します．

　0 1 0 0 0 1 0 0　符号0（プラス）で値が1000100
　　これは 十進法での「+68」を表す．
　1 1 1 1 1 0 1 1　符号1（マイナス）で値が1111011
　　これは十進法での「-5」を表す．

　このような値になるのは，最も右の桁のすぐあとに小数点を想定しているからです．すなわち最も右の桁が1の桁（これは十進法でも何進法でも同じです）その左が2の桁，その左が4の桁……となります．

　この方式ではある数より大きな数は表せません．上の絶対値が7ビットの方式だと，表せる最も大きな数はその7ビットが全部1で埋まった1111111で，これは十進法で表すと127です．なお表せる最も小さな数は-128ですが負の数の表現（2の補数表現）についてはここでは省略します．

　この方式を，次節で述べる浮動小数点方式に対して固定小数点方式と言います．

　もちろんこのままでは小数も表せませんが，小数を表すこと自体は固定小数点方式でも可能です．二進法の場合，たとえば右から2ビット目と3ビット目の間に小数点を置くと，小数点のすぐ右は$${\frac{1}{2}}$$（十進法での0.5）の桁，最も右が$${\frac{1}{4}}$$（同じく0.25）となります．もしさらにその右にもビットを置けば，$${\frac{1}{8}}$$（0.125），$${\frac{1}{16}}$$（0.0625）となります．

浮動小数点方式

　もちろん固定小数点方式でも，ビット数を増やせばより大きな数が表せますし，小数点以下の数についても上記の方法で表すことはできます．しかし，絶対値が非常に小さな数（ゼロに近い数）も含めた小数点付きの数や，逆に絶対値が非常に大きな数を表すのに適した別の方式「浮動小数点方式」があります．

　まず小数点付きの数は，たとえば

+0.5は　　　+5×$${\frac{1}{10}}$$　すなわち　+5×10⁻¹
-0.0625は　 -6.25×$${\frac{1}{100}}$$　すなわち　-6.25×10⁻²

と書けます．また絶対値が非常に大きな数は，

+2,000,000,000,000 は +2×1,000,000,000,000 すなわち +2×10⁺¹²
-425,000,000,000,000,000 は -425×1,000,000,000,000,000 すなわち -4.25×10⁺¹⁷

と書けます．この記法については，「化学基礎」などを学んだ人は「モル」に関して6.02214076×10²³（アボガドロ数）などと書かれていたのを覚えているかもしれません．

　これらの場合，「10」（「底」と呼びます）はどの数でも10を使うことにしているなら，そのつど記録しておく必要がありません．このことから

+0.5　は　+5と-1
-0.0625　は　-6.25と-2
+2,000,000,000,000　は　+2と+12
-425,000,000,000,000,000　は　-4.25と+17

という数のペアを覚えておけば元の数を復元できます．

　コンピュータで扱う場合は，上記の「10」ではなく「2」を使ったほうが都合がいいので，その方式を使っています．たとえば

+0.5 は　+1.0×$${\frac{1}{2}}$$ すなわち　+1.0×2⁻¹　なので　+1.0と-1
-0.0625は　-1.0×$${\frac{1}{16}}$$すなわち -1.0×2⁻⁴　なので　-1.0と-4

の2つの組で1つの数を表すわけです．

　これを浮動小数点方式と言います．2つの組の前者（+1.0と-1 なら+1.0の部分）を仮数部と，後者（-1の部分）を指数部と言います．

　ひとつ注意すべきなのは，浮動小数点方式には符号が2つあるということです．上の説明では仮数部に付けた符号は数全体が正か負かを示す符号ですが，そのほかに指数部にも符号があります．指数部の符号は数の正負とは無関係で，たとえば指数部が+3なら仮数部を2³倍すなわち8倍したものが，逆に指数部が-3なら仮数部を2⁻³倍つまり$${\frac{1}{2^3}}$$すなわち$${\frac{1}{8}}$$したものが，そして指数部が0なら仮数部そのままが，その数の値だ，という意味です．

　なお実際によく使われている方式（IEEE 754）⁴⁾では，指数部として符号を付けた数の代わりに少し違う表現（下駄ばき表現）が使われるのですが，表される指数部の数が負の数から正の数まであること自体は同じです．

　浮動小数点数についてより詳しくは参考文献5）の「第1章 情報のディジタル化 1.4 数値の符号化」に解説してあります．

　仮数部や指数部はそれぞれ何ビットかを使って表します．指数部を表すビットが多ければ，それだけ大きなプラスの数やマイナスの数まで表せます．仮数部を表すビットが多ければ，それだけ精度の高い数が表せます．

問題の解説

　問題全体は2ページにわたって書かれています．以下に全体を示します．

　以下，灰色の四角で囲んであるのはもとの問題の一部をそのまま再掲したものです．

問題の設定

　ここから問題を解説します．上で述べた浮動小数点方式の考え方をやや複雑にした方式を題材にしたものです．

　この問題で取り上げている方式について，問題文中では図1が示されています．まずこれについて解説します．

　この方式はビット長が8，すなわち8個のビットが並んでいますが，図1で示されているのはまず，最も左の1ビットは「符号」と呼び$${\textit{s}}$$と記す，その右の4ビットは「指数部」と呼び$${\textit{e}}$$と，最も右の3ビットは「仮数部」と呼び$${\textit{f}}$$とそれぞれ記すということです．そして指数部は「4ビット整数」，仮数部は「3ビット整数」（両方とも符号なし）として扱うということで，図1に示されている例だと，$${\textit{e}}$$の4ビット0101を整数として扱う，つまりこの4ビットの左からそれぞれ8,4,2,1の位となるのでこれは4+1=5，$${\textit{f}}$$は110で左から4,2,1の位となるのでこれは4+2=6，とそれぞれなります．$${\textit{s}}$$はそのまま0です．

　さて，その$${\textit{s, e, f}}$$から値がどう計算されるかは$${\textit{e}}$$の値により3つの場合に分かれ，数を表さない$${\textit{e}}$$が15の場合以外の2つはそれぞれ数式で示されています．

　両方の式とも，最初の部分は以下のようになっています．

$${(-1)^\textit{s}}$$

　$${\textit{s}}$$は1ビットだけなので0か1かです．(-1)⁰=+1で(-1)¹=-1ですから，このあとの式の値に対して+1か-1を掛けることになります．つまり$${\textit{s}}$$が0なら式の値はこの後ろの部分で計算された値そのまま，1なら後ろの部分で計算された値をマイナスにしたものになる，という意味になります．

　その後ろの部分は2つの式で異なり，指数部$${\textit{e}}$$の部分の値により，どちらが適用されるかが決まります．$${\textit{e}}$$は4ビットですから，0000すなわち0，0001すなわち1，…1111すなわち十進法で15，があり得ます．

とあるので，指数部$${\textit{e}}$$が0すなわち0000の場合はこの式が適用されます．いっぽう，

とあるので，$${0<\textit{e}<15}$$，つまり$${\textit{e}}$$が0と15以外の場合はこの式が適用されます．

　そしてℯが15すなわち1111の場合は「数を表さない」となっています．数式で表される2つの場合について以下で解説します．

ℯが0の場合

　まず$${\textit{e}}$$が0の場合です．この場合は

ですが，この式は，すでに述べた符号を決める最初の部分を取り除くと

です．仮数部$${\textit{f}}$$は3ビットですから，000から111まで，すなわち0から7までのいずれかになります．これに2⁻⁸すなわち$${\frac{1}{2^8}}$$つまり$${\frac{1}{256}}$$を掛けた数になるので，

　$${\textit{f}}$$が0なら$${\frac{0}{256}}$$すなわち0，　※1
　$${\textit{f}}$$が1なら$${\frac{1}{256}}$$　　※2

…となり，

　$${\textit{f}}$$が7なら$${\frac{7}{256}}$$　　※3

で，この間の数を$${\frac{1}{256}}$$刻みで表せます．

　$${\frac{1}{256}}$$は$${\frac{4}{1024}}$$ですから十進法の0.004ぐらいの刻みで0から$${\frac{7}{256}=\frac{28}{1024}}$$まで表せる方式です．

　ビット列が00000110ですから，図1に従って分解すると0と0000と110の3つに分けられます．最初の0は符号$${\textit{s}}$$に対応するので$${\textit{s}=0}$$です．その次の0000は指数部$${\textit{e}}$$で，0000は二進法整数で0なので$${\textit{e}=0}$$となり最初の式$${(-1)^{\textit{s}} \times \textit{f} \times 2^{-8}}$$が適用されることになります．最後の110は仮数部$${\textit{f}}$$で，110は二進法整数で6なので$${\textit{f}=6}$$です．$${\textit{s}=0}$$と$${\textit{f}=6}$$を$${(-1)^\textit{s} \times \textit{f} \times 2^{-8}}$$にそれぞれ代入すると，$${(-1)^\textit{s} \times \textit{f} \times 2^{-8}=(-1)^0 \times 6 \times 2^{-8}=1 \times 6 \times \frac{1}{2^8}=\frac{6}{256}=\frac{3}{128}}$$となります．

　なお問題文中に$${e=0000_{(2)}}$$などとありますが，この$${_{(2)}}$$は，その前に書いてある$${0000}$$が二進法での表記だという意味です．

　さて，ここまでは説明でしたが，ここで最初の問題が出てきます．

　この$${\textit{e}}$$=0の場合，すでにこの節の最初のほうで述べたように，$${\textit{f}}$$が0なら$${\frac{0}{256}}$$すなわち0，$${\textit{f}}$$が1なら$${\frac{1}{256}}$$……となり，$${\frac{7}{256}}$$までの数が表せますから，※3で示したように，最も大きな数は$${\textit{f}}$$が7の場合なので【ア】は7，その場合の値は$${\frac{7}{256}}$$なので【イ】は$${\frac{7}{256}}$$です．なお【イ】は既約分数となっていますが，7と256に公約数はありませんから$${\frac{7}{256}}$$のままが正解です．

ℯが1から14までの場合

　こんどは$${\textit{e}}$$が0ではなく1から14までの場合です．この場合は

で，符号を決める最初の部分を取り除くと

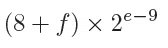
です．

　たとえば$${\textit{e}}$$が1の場合，$${(8+\textit{f}) \times 2¹⁻⁹=(8+f) \times 2⁻⁸}$$となり，仮数部$${\textit{f}}$$は000から111まで，すなわち0から7までのいずれかなので，

　$${\textit{f}}$$が0の場合は$${(8+0)×2^{-8}=8×\frac{1}{2^8}=\frac{8}{256}=\frac{1}{32}}$$
　$${\textit{f}}$$が1の場合は$${(8+1)×2^{-8}=9×\frac{1}{2^8}=\frac{9}{256}}$$
　…
　$${\textit{f}}$$が7の場合は$${(8+7)×2^{-8}=15×\frac{1}{2^8}=\frac{15}{256}}$$

となります．

　$${\textit{e}}$$が2の場合は，$${(8+\textit{f}) \times 2²⁻⁹=(8+f) \times 2⁻⁷}$$となり，

　$${\textit{f}}$$が0の場合は$${(8+0)×2^{-7}=8×\frac{1}{2^7}=\frac{8}{128}=\frac{1}{16}}$$
　…
　$${\textit{f}}$$が7の場合は$${(8+7)×2^{-7}=15×\frac{1}{2^7}=\frac{15}{128}}$$

となります．

　$${\textit{e}}$$が15の場合は数を表さないとなっていますから，最も大きい14の場合は，$${(8+\textit{f}) \times 2^{14-9}}$$=$${(8+\textit{f}) \times 2^5}$$となり，

　$${\textit{f}}$$が0の場合は$${(8+0)×2⁵=8×32=256}$$
　…
　$${\textit{f}}$$が7の場合は$${(8+7)×2⁵=15×32=480}$$　※4

となります．

　00101110は0と0101と110の3つに分けられ，図1から，最初の部分は符号$${\textit{s}}$$が0であることを，次の部分は指数部$${\textit{e}}$$が0101すなわち5であることを，最後の部分は仮数部$${\textit{f}}$$が110すなわち6であることを表すことが分かります．$${\textit{e}}$$が0でも15でもないので2番目の式が適用され，

$${(-1)^0×(8+6)×2^{5-9}=1×14×2^{-4}=14×\frac{1}{2^4}=\frac{14}{16}=\frac{7}{8}}$$

となります．

　さて問題です．

　これを求めるために，

をあらためて見直してみましょう．全体は$${(8+\textit{f})}$$と$${2^{e-9}}$$の掛け算ですから，その両方とも最も小さくなるようにすればよいです．まず$${(8+\textit{f})}$$を最小にするためには$${\textit{f}}$$を最小つまり0にすればよいですね．なので【エ】の答は0です．

　一方の$${2^{e-9}}$$を最小にするためには$${\textit{e}-9}$$を最小にすればよい，ならば$${\textit{e}}$$は0にするのがよい……と思った人は，これは$${0<\textit{e}<15}$$つまり$${\textit{e}-9}$$が1から14までの場合についての問題なのだ，という問題設定をもう一度見てください（それに$${\textit{e}}$$が0だと適用される式がこれでなく前節「$${\textit{e}}$$が0の場合」で述べたものになってしまいます）．なので$${\textit{e}}$$はこの範囲内の最小すなわち1で，これが【ウ】の答です．

　このときの値【オ】は，

の$${\textit{e}}$$に1を，$${\textit{f}}$$に0を，そして$${\textit{s}}$$に0を代入し，

　　　$${(-1)^0×(8+0)×2^{1-9}=8×2^{-8}=\frac{8}{256}=\frac{1}{32}}$$

です．これは

　　　$${8×2^{-8}=2^3×2^{-8}=2^{3-8}=2^{-5}=\frac{1}{2^5}=\frac{1}{32}}$$

という計算もできます．

　なお，

に出てくる$${(8+\textit{f})}$$でなぜ$${\textit{f}}$$に8を足すか（逆に言えば，なぜもともとの仮数部の値から8を引いた数を$${\textit{f}}$$としているのか）は，浮動小数点方式で「ケチ表現」と言われる方式と関係しています．また$${2^{\textit{e}-9}}$$でなぜ$${\textit{e}}$$から9を引くのか（それにより【ウ】【エ】【オ】で問われているように$${\textit{e}}$$を1にすると最小$${\frac{1}{32}}$$を表現できます）は，同じく「下駄ばき表現」と言われる方式と関係しています．これらについて学んでみたい人は，参考文献3）や4）のうちこれらについて書かれた部分を読んでみてください．

0を表すビット列

　次はこの問題を考えます．値が0になるのは，以下の2種類のどちらかの場合にその式の値が0となる，という場合です．

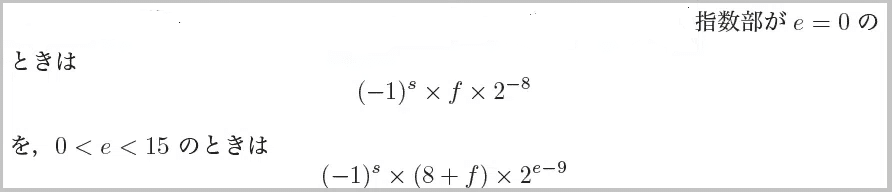
　まず，2番目の式

を0にすることができるかを見てみましょう．全体は3つのものの掛け算ですから，そのどれかが0になれば式の値も0になります．

は$${\textit{s}}$$が0なら+1，$${\textit{s}}$$が1なら-1，なので0にはなりません．また，$${\textit{f}}$$は0から7までのどれかなので，

　　　　　　　　　　$${（8+\textit{f}）}$$

も0にはできません．さらに

も ，$${\textit{e}}$$をいくつにしても 0にはなりません．（2⁰は0でなく1です．問題の設定をいったん忘れて，たとえば$${2^{-1000000}}$$としてみても，これは$${\frac{1}{2^{1000000}}}$$のことなので，0に近い数ではありますがやはり0ではありません）．なのでこの2番目の式は決して0にはならない，ことが分かります．

　ではこんどは，$${\textit{e}}$$が0の場合に適用される最初の式，

について考えてみましょう．これも，全体は3つのものの掛け算ですから，そのどれかが0になれば式の値も0になります．

　$${\textit{f}}$$を0すなわち000にしてみると，それで式の値は0になります．なお実はこれは上の「$${\textit{e}}$$が0の場合」の※1ですでに示してあります．

　他の2つの項については，

は0にならないことは上に書いたとおりですし，また，

　　　　　　　　　　　　2⁻⁸

は定数なので変えようがなく0にはなりません．

　ここまでをまとめると，式の値が0になるのは$${\textit{e}}$$が0すなわち0000で最初の式が適用され，かつ$${\textit{f}}$$が0すなわち000の場合しかありません．ところがこの問題は「2つ答えよ」となっています．どうしたらいいのでしょう．

　実はその答えは，最初の式の中の

にあります．これは$${\textit{s}}$$が0なら+1，$${\textit{s}}$$が1なら-1になる項ですが，$${\textit{f}}$$が0だとどちらであっても式の値は0です．

　したがって，$${\textit{f}}$$は0とし，$${\textit{e}}$$も0の場合だけこの式が適用されますからもちろん0にする，そして$${\textit{s}}$$は0の場合と1の場合の両方があります．

　なのでビット列としては，

0 0000 000　および　1 0000 000

であり，これが（3）の答えです．

最も小さな正の数

　次はこの問題です．こんどは上記の0は除き，この方式で表せる正の数のうち最も小さな数，という問題です．

　実はすでにこれは上で解説してあります．$${\textit{e}}$$が0の場合について「$${\textit{e}}$$が0の場合」で，$${\textit{e}}$$が1以上の場合について「$${\textit{e}}$$が1から14までの場合」で，すでに値はどうなるか解説してあります．これを見直すと，その中で正の値で最も小さいのは※2で示すものです．

　この※2は，$${\textit{e}}$$が0すなわち0000，$${\textit{f}}$$が1すなわち001です．$${\textit{s}}$$は，正の数ですから0です．この3つから

　0 0000 001

が答えのビット列です．値も※2に示してある$${\frac{1}{256}}$$が答えです．

1より大きい中で最も小さな数

　こんどは，「1よりも大きい中で最も小さな数」です．1より大きいので当然正の数なので，$${\textit{s}}$$は0です．以下では$${(-1)^\textit{s}}$$の部分を除いて考えてみましょう．

　まず，ちょうど1を表す式を考えてみましょう．2つの式のうち最初の式は，符号の部分を除くと

で，$${\textit{f}}$$は0から7までのどれかですから，「$${\textit{e}}$$が0の場合」の※3にあるように，最大でも$${\frac{7}{256}}$$なので「1よりも大きい」数にはなりません．

　いっぽう，もう1つの式は，符号の部分を除くと

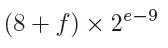
で，$${\textit{f}}$$を0にすると　$${(8+0) \times 2^{\textit{e}-9}}$$すなわち$${8 \times 2^{\textit{e}-9}}$$です．

　ここで，$${8×\frac{1}{8}}$$というものを考えてみると，これは1になります．$${\frac{1}{8}}$$は2⁻³ですから，$${\textit{e}}$$を6にすると，$${2^{\textit{e}-9}}$$=2⁶⁻⁹=2⁻³になります．なので，ちょうど1にするためには，$${\textit{f}}$$を0，$${\textit{e}}$$を6にすればいいことが分かります．

　しかしこの問題は「1より大きい中で最も小さな数」です．

を見ると，$${\textit{f}}$$も$${\textit{e}}$$も，どちらも増やせば式の値は大きくなるので，この片方を1だけ増やすことで答えは求められるという見当がつきます．

　$${\textit{f}}$$を増やして0から1にすると，この式は

　　$${(8+1)×2^{6-9}=9×2^{-3}=\frac{9}{8}}$$　※5

です．一方$${\textit{e}}$$を増やして6から7にすると

　　$${(8+0)×2^{7-9}=8×2^{-2}=\frac{8}{4}=2}$$

です．両方とも1より大きいですが，この2つのうち小さいのは$${\frac{9}{8}}$$なのでこれが（5）で求めている値です．既約分数でという問題ですが，$${\frac{9}{8}}$$のままで既約分数です．

　※5の式では，$${\textit{f}}$$は1すなわち001，$${\textit{e}}$$は6すなわち0110です．そしてこの数は正の数ですから$${\textit{s}}$$は0にします．なのでビット列は，

　0 0110 001

が答えです．

最も大きい値

　こんどは「最も大きい値を表すビット列」です．これも，「$${\textit{e}}$$が0の場合」と「$${\textit{e}}$$が1から14までの場合」を見直してもらうとすでに解説してあり，答えはその中で最も大きな値になる※4で，値は480です．

　この場合$${\textit{e}}$$は14すなわち1110，$${\textit{f}}$$は7すなわち111で，$${\textit{s}}$$は正の数ですから0です．なのでビット列は

　0 1110 111

です．

この解説について

　ここまで読んでどうだったでしょうか．この解説は，このような浮動小数点方式，あるいはもっと一般的に数値等のデジタル表現にあまり習熟していない人を対象に，初学者にも自分で読んで理解できるように細かく解説したつもりです．

　このようなデジタル表現やプログラミングの勉強を教えていて，最初問題を見たときは分からないと言っていたのに，その人に合わせて一歩ずつ学んでもらったあとでは「なんでこれが最初はあんなに難しく思えたんだろう」という学生を筆者は何人も見てきました．筆者だけでなく，プログラミングを勉強したあと「プログラミングに対する意識やイメージが変わりました」と生徒がアンケートに書いていたとおっしゃっていた先生もいます．

　この文章を読む人に一人ひとり筆者が直接教えることはできませんが，しかしきちんとこの文章を読んでもらえば，それに近い勉強ができるように，この文章は書いたつもりです．これを読んでいるあなたの勉強に活用してもらって「なんでこれが最初はあんなに難しく思えたんだろう」とあとで思ってもらえればうれしいです．

参考文献
1）電気通信大学：入試情報 情報理工学域一般選抜前期日程「情報」試作問題，サンプル問題についてhttps://www.uec.ac.jp/news/admission/2024/20240722_6390.html
2） 佐藤　喬：教科「情報」の入学試験問題って？　電気通信⼤学 試作問題 第3問 数字列の並び替え，情報処理，Vol.65，No.6，pp.e34-e43（June 2024）．　https://doi.org/10.20729/00234181
3）Wikipedia：浮動小数点数，2024年8月15日閲覧．
4）Wikipedia：IEEE754，2024年9月9日閲覧．
5）河村一樹，和田　勉，山下和之，立田ルミ，岡田　正，佐々木整，山口和紀：IT Text 一般教育シリーズ 情報とコンピュータ，オーム社（2011），ISBN978-4-274-21086-0

（2024年8月17日受付）
（2024年9月18日note公開）

■和田　勉（正会員）
長野大学教職課程高等学校情報科非常勤講師・元教授，元・大韓民国高麗大学師範学部コンピュータ教育学科招聘教授．本会情報入試委員会・初等中等教育委員会・一般情報教育委員会委員・会誌編集委員会教育WG専門委員．学会活動貢献賞受賞，本会シニア会員．

情報処理学会ジュニア会員へのお誘い
小中高校生，高専生本科～専攻科1年，大学学部１～3年生の皆さんは，情報処理学会に無料で入会できます．会員になると有料記事の閲覧，情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります．ぜひ，入会をご検討ください．入会はこちらから！