
「確率モデルのシミュレーション」は,問題設定を楽しみながら解こう!

林 宏樹(雲雀丘学園中学校・高等学校)
今回は,令和4年(2022年)11月9日に大学入試センターより公開された「情報」の試作問題 ¹⁾ の第2問Bのシミュレーションを扱った問題を解説します.分野としては情報Ⅰ(3)コンピュータとプログラミングの位置づけであり,この分野にはモデル化とシミュレーションも含まれてます.
まず,シミュレーションって言葉を聞くと,難しそうだと感じてしまいます.シミュレーションの問題のポイントは,「問題文の内容が,図のどの部分を表現しているか」を読み取ることです.
問題設定の理解
まずは,問題設定が書かれています.リード文には大切なヒントが書かれています.しかし,一度読んだだけで完璧に理解する必要はありません.一度読んで,問題を読み進めていき,理解できないところがあれば戻ることを心がけましょう.

この問題のリード文では,次の4つの状況を把握するぐらいでいいです.
文化祭の場面でお客を待たせることが多いこと
待ち状況をシミュレーションすること
お店では同時に一人の客しか対応できないこと
客が注文できるクレープは一枚のみであること
ただ,この段階では,どの情報が必要であるのかわかりませんので,読み進めます.

問題文に太字が含まれています.ここがポイントになりそうだと勘づいた人は鋭いです.シミュレーションの分野ですから,数値が出たらチェックです.青下線部では表1の内容が書かれています.ここは,まず表1を見て,わからない部分があれば戻ってもう一度読むという心構えで十分です.


10人の到着間隔が表2に示されています.さて,ここで,10人目の(ケ)の数値を求めます.「生成させた乱数」と「到着時間」の関係を読み解きましょう.「生成させた乱数」を小さい順に並べてみると,
0.11→0分,0.28→2分,0.31→2分,0.41→2分,0.43→3分
となっています.「0.41→2分,0.43→3分」で変化している部分が気になりますね.ここで,表1を見ながら,数値を読み解きます.すると,「階級値2分の累積度数が0.42」となっていることから,「生成させた乱数→前の累積相対度数より大きく,累積相対度数より小さい」ならば,「到着間隔→階級値」となっていることに気づくことができます.
したがって,この規則性から「0.95」は,0.94より大きく,0.96より小さいですから,「8分」(ケの解答)とわかります.
(ケの解答)8
シミュレーションの実行
次に,具体的なシミュレーションに進みます.
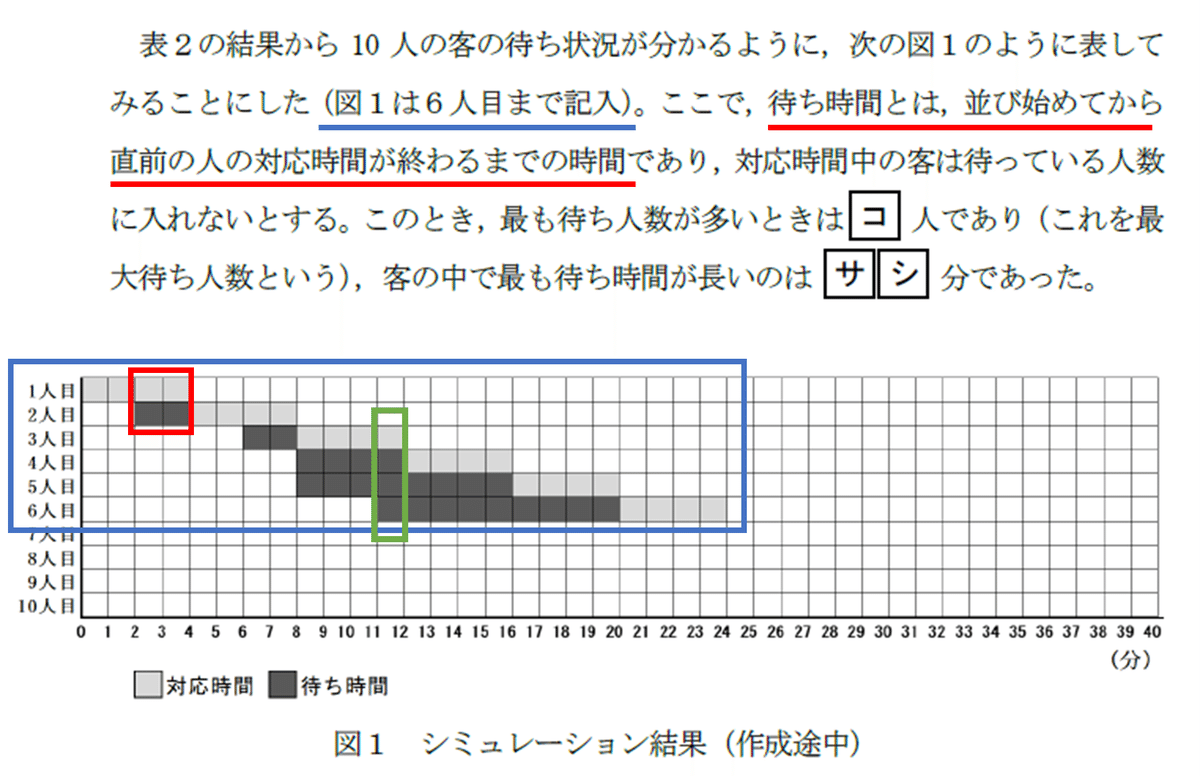
青下線部から,図1-1の青枠の部分のことであることを読み取ることはできましたか? 6人目までしか書かれていないようです.赤下線部から,2人目が赤枠の個所で待っている(待ち時間)となっていることを読み取ることができます.シミュレーションでは,リード文の説明が図(出力)のどの部分を表しているのか読み取ります.すると,緑枠の個所では,4人目,5人目,6人目の3人が待っていることがわかります.
では,問題に取り組みます.(コ)が最大の待ち時間,(サシ)が最も長い待ち時間です.では,自分でシミュレーションしてみます.まず,「到着間隔」の理解が重要です.

「到着間隔」ということから,
1人目が到着してから2マス(2分後)に2人目が到着する(オレンジの部分)
2人目が到着してから4マス(4分後)に3人目が到着する(青の部分)
3人目が到着してから2マス(2分後)に4人目が到着する(黄緑の部分)
4人目が到着してから0マス(0分後)に5人目が到着する(黄緑の部分)
5人目が到着してから3マス(3分後)に6人目が到着する(黄の部分)
となることを読み取る必要があります.さらに,図1におけるリード文を思い出しますと,赤矢印で示したところが,一人の客の対応時間4分を表していることがわかります.
よって,7人目は,到着間隔が3分ですから,図1-3のように表現できます.
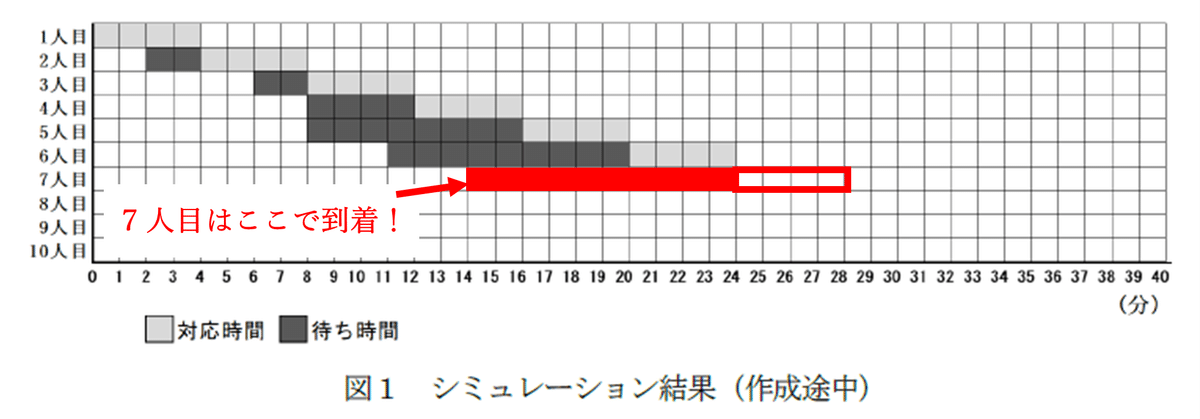
続いて,8人目,9人目,10人目をシミュレーションしてみます.
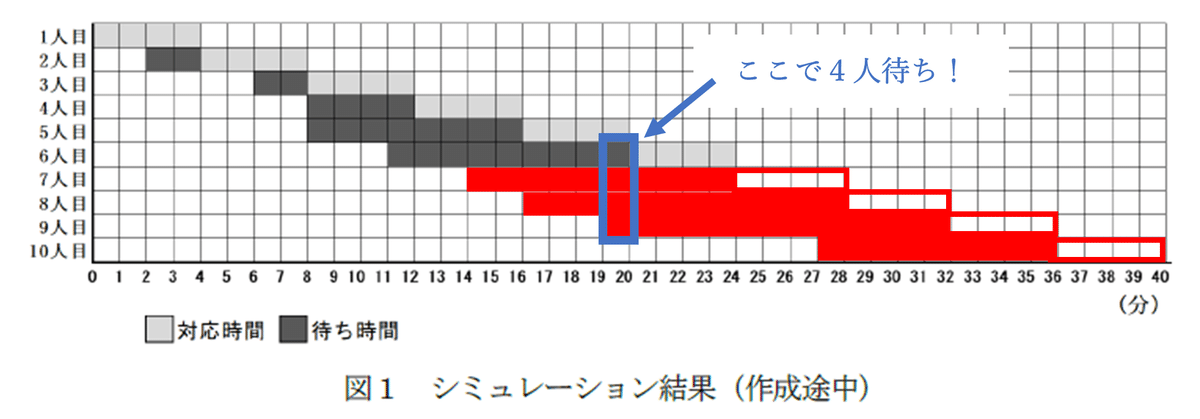
図1-4のように,自分でシミュレーションします.すると,灰色塗りは対応時間であり,黒塗り・赤塗りの縦列(青色の部分)が待っている人ですから,19-20の間で4人待っていることがわかります.また,待っている時間は,黒塗り・赤塗りの横を計算すると,19-32の間で9人目が13分待っていたことがわかります.このように,問題文を読み取り,ルールを把握し,自分でシミュレーションする問題です.
(コの解答)4
(サシの解答)13
シミュレーション結果の読み取り

来客数が10人,20人,30人,40人の場合のシミュレーションの結果です.グラフでは必ず横軸,縦軸の項目をチェックします.横軸は最大待ち人数,縦軸は回数です.

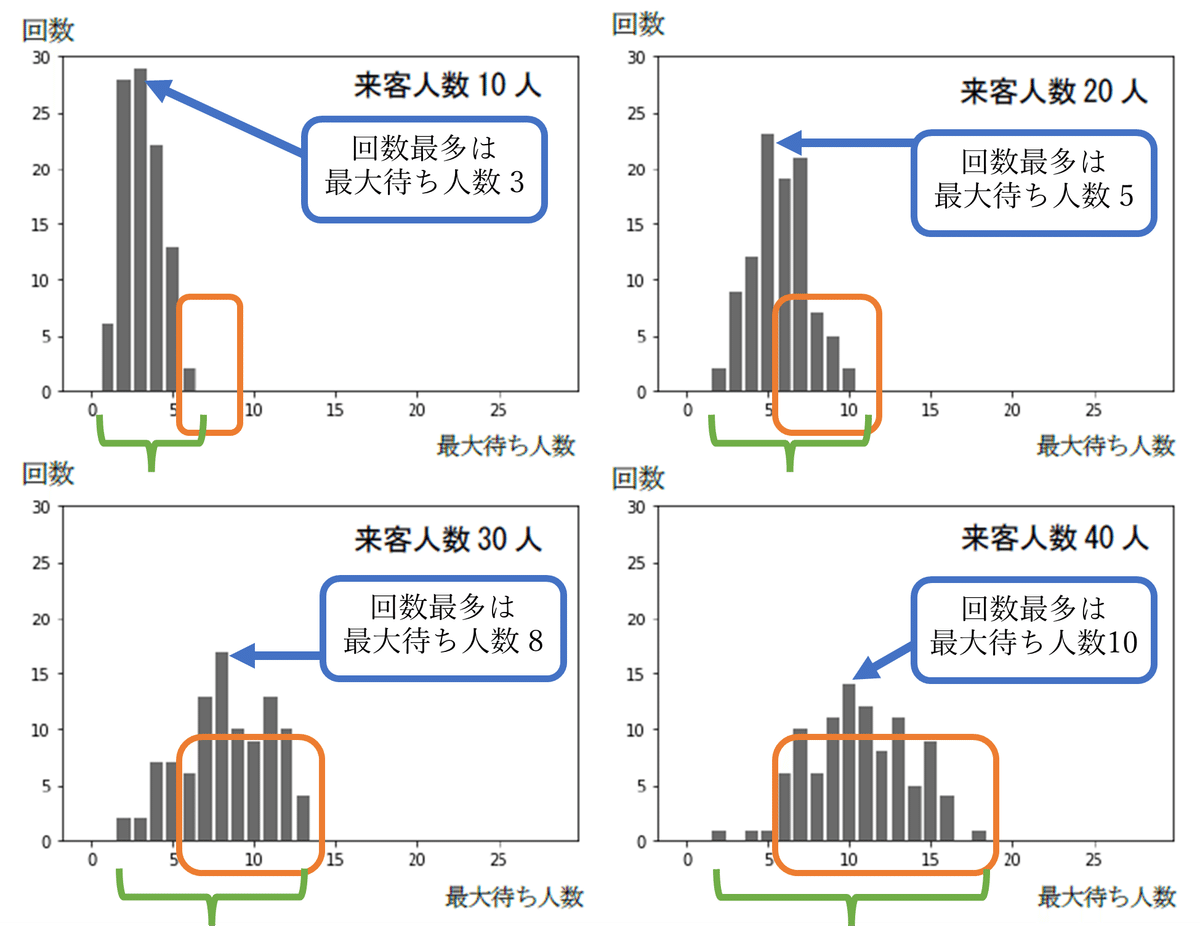
シミュレーション結果の特徴的な部分を図2-1に示しました.
選択肢⓪は,オレンジ色の変化を見ると,最大待ち人数が増えていることがわかる(正しい).
選択肢②は,青色の個所を見ると,最大待ち人数は来客人数の1/4前後の人数の頻度が高くなっていることがわかる(正しい).
選択肢③は,黄緑色の幅の変化を見ると,散らばりが大きくなっていることがわかる(正しい).
そして,選択肢①は,来客人数が10人のとき,最大待ち人数が6人の場合があるため,「半数以下に収まっている」のは正しくない.
(スの解答)1
改善のシミュレーション
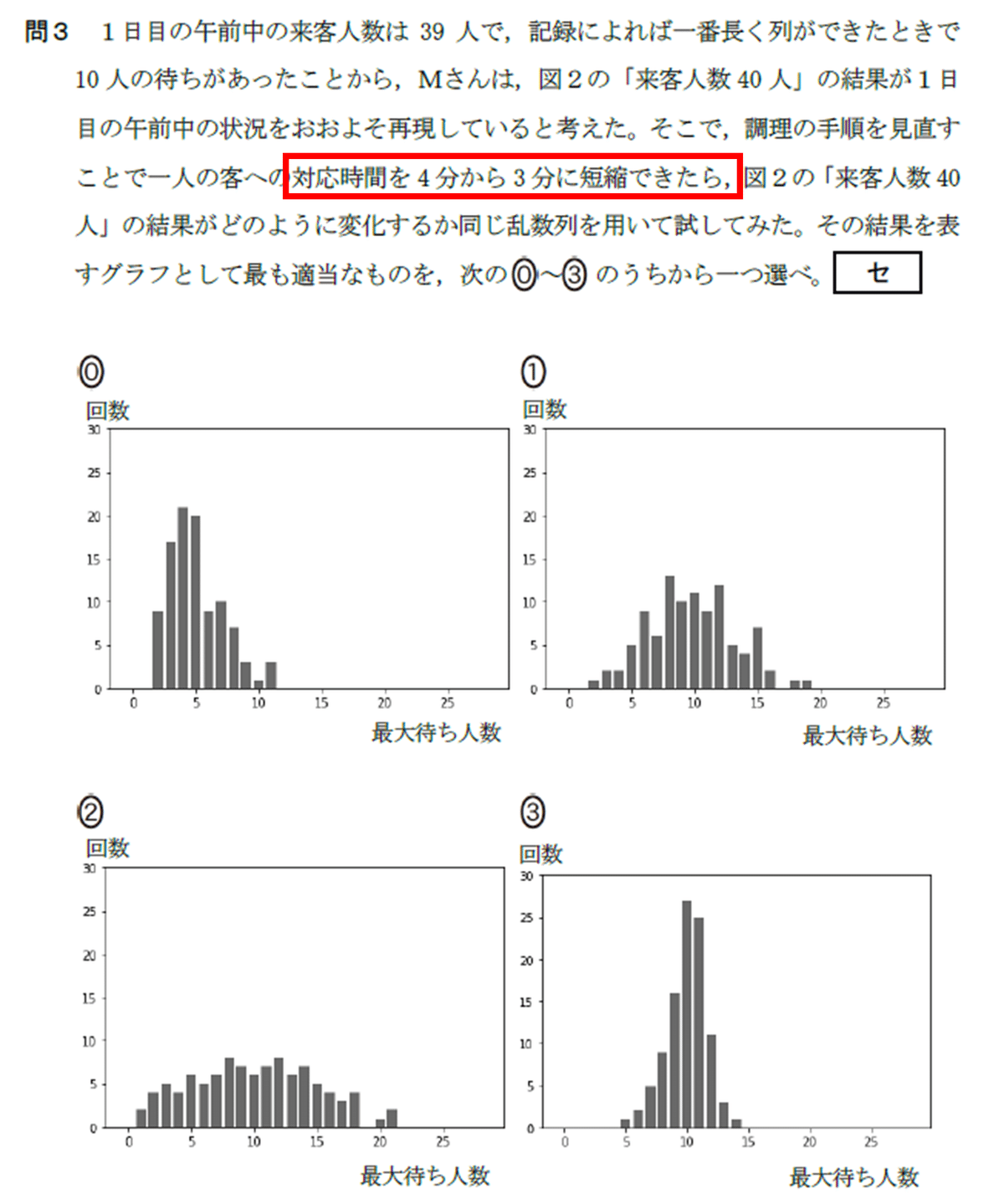
問3の問題文から,4分から3分に改善された(赤枠)と読み取る必要があります.すると,図2右下の図(来客人数40人)と比較して改善されている,つまり,散らばりは小さくなったり,分布の最大待ち人数が小さい方に変化することが想定できます.今回は散らばりや分布に着目してみます.
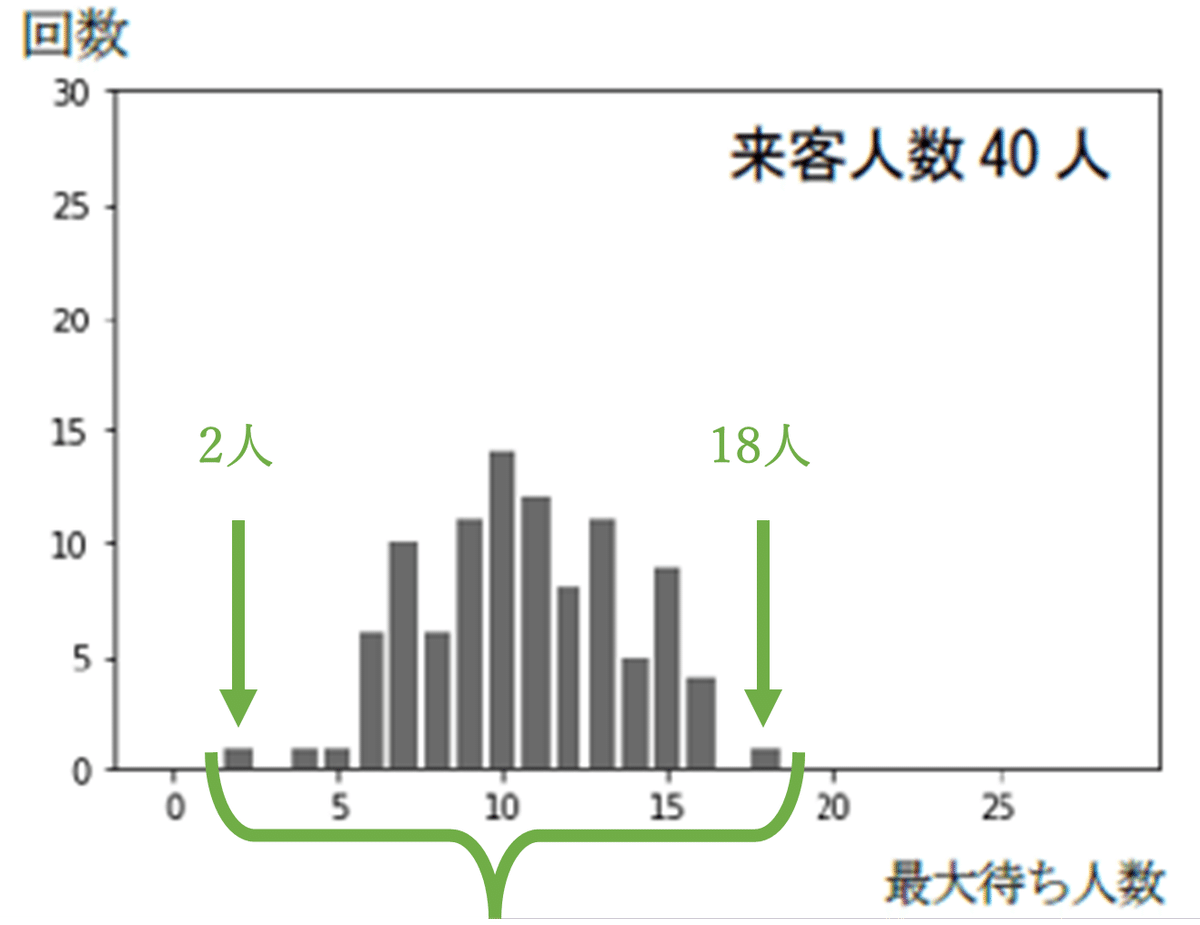
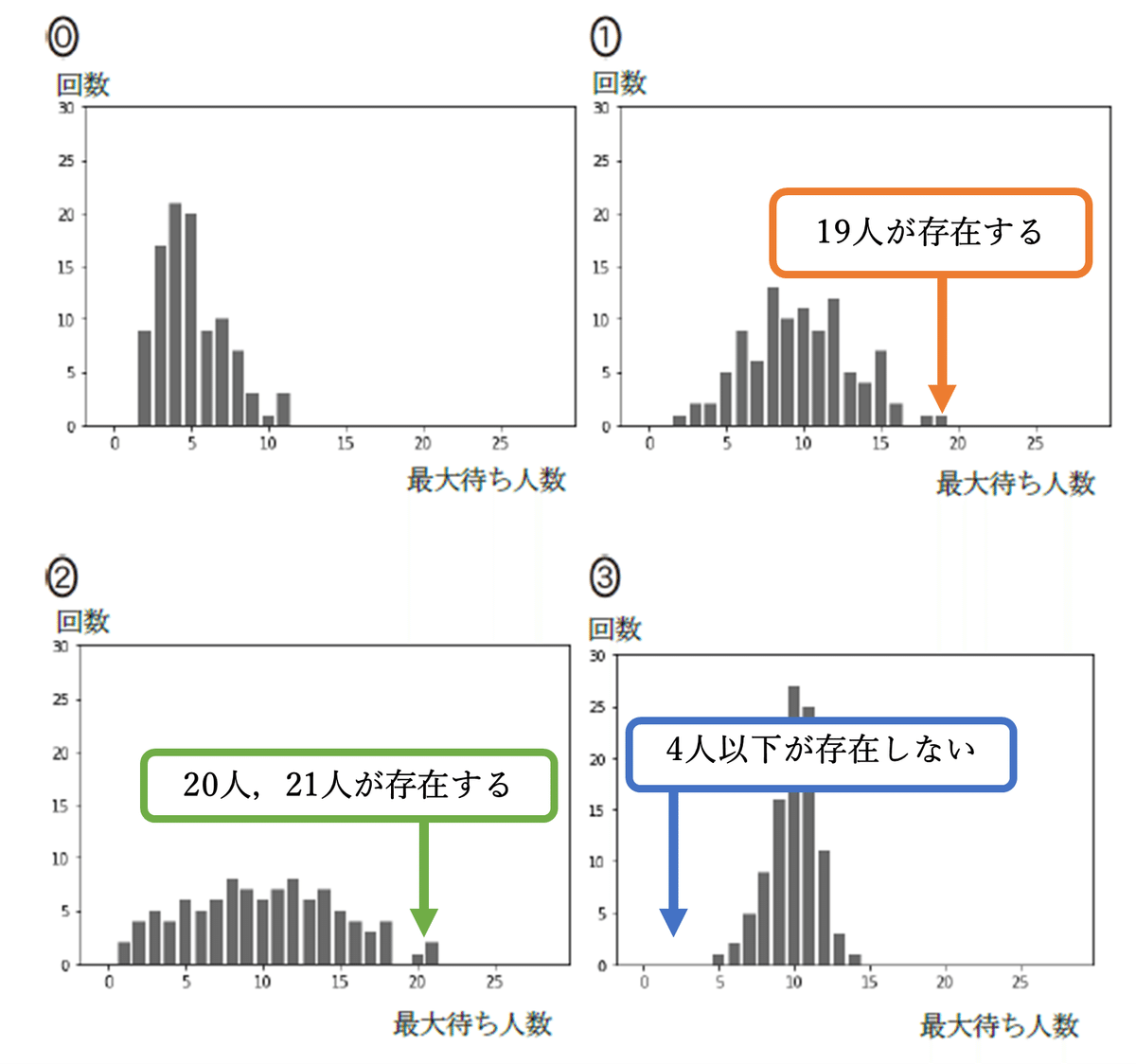
図2-2(改善前)と比較すると,
選択肢①と②は,最大待ち人数が18人より多くなっている
選択肢③は,4人以下がおらず不自然な分布になっている
とわかり,これらは不適切であると判断できます.よって,選択肢⓪は,最大待ち人数が小さい方に変化しており,改善が見られると判断できますね.
(セの解答)0
情報Ⅰを活かした探究活動の充実
大学入学共通テストの試作問題のシミュレーションの問題を解説しました.シミュレーションという用語は難しそうと感じますが,きちんと問題文を読めば納得のいく流れであることがわかります.
令和4年度から実施されている学習指導要領の特徴の1つとして,探究活動の充実が挙げられます.今回の問題は,文化祭の場面での事例でした.問題を解き終わってから改めて見ると,「情報Ⅰ」で学んだ知識・技能を用いて培った思考力によって,多くの高校生が実行可能な探究活動の事例となっています.情報教育が試験対策とならず,情報的思考力を身に付けられる授業作りが求められています³⁾.
「情報Ⅰ」での学びは,教科内だけでとどめるのではなく,日常生活における活用,探究活動における活用によって,学びを深化させることが期待できます.近年では中高生情報学研究コンテスト²⁾ という情報技術を活用した探究活動の全国大会が開催されています.私が指導する生徒においても,全国規模のコンテスト入賞を目指し,自主的に高度な情報技術を学習したいという生徒が増えています.
今後,大学入学共通テストに出題される題材をきっかけに,教科「情報」の学びが日常生活を過ごす上で有用であることを伝え,さらには情報技術を活用した探究活動を行う高校生の育成に貢献していきたいと考えています.
参考文献
1)大学入試センター:令和7年度試験の問題作成の方向性,試作問題等
https://www.dnc.ac.jp/kyotsu/shiken_jouhou/r7/r7_kentoujoukyou/r7mondai.html
2)中高生情報学研究コンテスト:https://www.ipsj.or.jp/event/event_chukousei.html
3)稲垣俊介:大学情報入試の動向:4. 高等学校から見た情報入試,情報処理,Vol.65,No.2,pp.e14-e16 (2024).
https://doi.org/10.20729/00231770.
(2023年10月18日受付)
(2024年1月15日note公開)
■林 宏樹(正会員)
雲雀丘学園中学校・高等学校(兵庫県宝塚市).情報科主任・数学科・探究科教諭.高等学校「情報」実践事例集原稿執筆.JDSSP高等学校データサイエンス教育研究会主査(https://ds-education.com/).
情報処理学会ジュニア会員へのお誘い
小中高校生,高専生本科~専攻科1年,大学学部1~3年生の皆さんは,情報処理学会に無料で入会できます.会員になると有料記事の閲覧,情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります.ぜひ,入会をご検討ください.入会はこちらから!
