
【麻雀】安定段位をベイズ推定する
はじめに
天鳳・雀魂といったネット麻雀の世界では、プレイヤーの実力を表す指標のひとつとして安定段位が利用されています。安定段位は長期的には何段で安定できるかを表す指標で、たとえば天鳳の安定段位が8段なら、鳳凰卓で数多く打つと8段で安定すること意味します。安定段位は「段位」として解釈できるというわかりやすさから、最も利用されている実力指標のひとつになっています。
安定段位の「安定」は長期的にはこの段位で「安定」するという意味なので、少ない試合数では実はあまり「安定」しません(安定段位の安定性、つまり標準誤差に関しては別の記事で書く予定です)。なので、少ない試合数でプレイヤー1とプレイヤー2の安定段位を比較しても、どちらが強いか確定的なことは言えません。なら試合数が多ければいいのかというと、2000試合なら比較していいとか、いや5000試合必要だ、みたいな議論も行われています。もちろん試合数が多ければ多いほど安定段位の信頼性は上がっていきますが、結局2000試合なら2000試合なりの、5000試合なら5000試合なりの不確実性は残ります。
とはいえ、500試合ような少ない試合数でも結果は結果なわけで、「500試合の結果からは何もわかりません」というのも極端な姿勢に思えます。もちろん少ない試合数だと不確実性が強く残りますが、それでもなんらかの参考情報にはなるはずです。この記事では、不確実性を考慮しながら「安定段位が8段を超えている確率はxxx%」「プレイヤー1のほうが強い確率はxxx%」のように確率的な主張ができることを目指します。
たとえば、
プレイヤー1:500戦で順位率が$${(0.29, 0.26, 0.23, 0.21)}$$の安定段位10段
プレイヤー2:3000戦で順位率が$${(0.27, 0.26, 0.25, 0.22)}$$の安定段位8.9段
という2人のプレイヤーがいたとして、どちらが強い可能性が高いでしょうか?プレイヤー1は単なる確変かもしれませんが、とはいえある程度実力も反映されていると思われます。プレイヤー2の安定段位は相対的に信頼できますが、それでもある程度の不確実性も残っています。このように両プレイヤーの戦績には不確実性があるわけですが、それを考慮しながら「プレイヤー1が強い確率は30%」のように答えられることを目指します。
安定段位をベイズ推定する
設定
以降、確率分布のパラメータはギリシャ文字で、ベクトルは太字で表記します。プレイヤーの順位率を$${\bm{\theta} = (\theta_1, \theta_2, \theta_3, \theta_4)}$$で表すとします。つまり、$${\theta_k}$$はこのプレイヤーが$${k}$$位になる確率です。この順位率から生成された着順を確率変数$${X \in \{1, 2, 3, 4\}}$$とします。このとき、$${X = k}$$になる確率は単純に$${\theta_k}$$になります。あとで便利なので、順位率が与えられたときの着順$${X}$$の確率質量関数を以下のように表します。
$$
\newcommand{\paren}[1]{\left(#1\right)}
\newcommand{\vtheta}{\bm{\theta}}
\newcommand{\prodk}{\prod_{k=1}^4}
\newcommand{\one}[1]{\bm{1}\left\{#1\right\}}
\newcommand{\Cat}{\mathrm{Categorical}}
P(X \mid \vtheta) = \Cat\paren{X \mid \vtheta} = \theta_k^{\one{X = k}}
$$
これはカテゴリカル分布と呼ばれています。
プレイヤーが$${N}$$試合行った結果を$${\bm{X} = (X_1, \dots, X_i, \dots, X_N)}$$で表すとします。いま考えたいのは、データ$${\bm{X}}$$が与えられたときの順位率に対する分布$${P(\bm{\theta} \mid \bm{X})}$$です。データが与えられたあとの分布なので、これは事後分布と呼ばれています。$${\bm{\theta}}$$の事後分布がわかれば、そこから安定段位の分布を導くことができます。
ところで、事後分布$${P(\bm{\theta} \mid \bm{X})}$$はベイズの定理から以下のように変形できることが知られています。
$$
\newcommand{\vX}{\bm{X}}
\newcommand{\vtheta}{\bm{\theta}}
\begin{align*}
P(\vtheta \mid \vX) &= \frac{P(\vX \mid \vtheta)P(\vtheta)} {P(\vX)}
\end{align*}
$$
事後分布を求めるためのパーツがわかったので、それぞれ確認していきましょう。
尤度
まず、$${P(\bm{X} \mid \bm{\theta})}$$は順位率$${\bm{\theta}}$$が与えられたときの$${N}$$試合の結果の確率分布になります(ちなみにこれは尤度と呼ばれています)。先程、1試合の結果の確率分布は$${ \theta_k^{\bm{1}(X = k)} }$$になることを確認したので、それの$${N}$$試合を考えればよさそうです。
話を簡単にするために、試合の結果は互いに独立に同じ分布から生成されているとします。つまり、流れがないことと、実力が一定であるという仮定をおきます。このとき、$${N}$$試合の結果が従う分布は
$$
\newcommand{\paren}[1]{\left(#1\right)}
\newcommand{\one}[1]{\bm{1}\left\{#1\right\}}
\newcommand{\vX}{\bm{X}}
\newcommand{\vtheta}{\bm{\theta}}
\newcommand{\valpha}{\bm{\alpha}}
\newcommand{\Cat}{\mathrm{Categorical}}
\newcommand{\Dir}{\mathrm{Dirichlet}}
\newcommand{\sumi}{\sum_{i=1}^N}
\newcommand{\prodi}{\prod_{i=1}^N}
\newcommand{\prodk}{\prod_{k=1}^4}
\begin{align*}
P(\vX \mid \vtheta)
&= \Cat\paren{\vX \mid \vtheta} \\
&= \prodi\prodk \theta_k^{\one{X_i = k}}\\
&= \prodk \theta_k^{\sumi \one{X_i = k}}\\
&= \prodk\theta_k^{N_k}
\end{align*}
$$
となることがわかります。ここで、$${k}$$位をとった回数$${\sum_{i=1}^N \bm{1}(X_i = k)}$$を表記の単純化のため$${N_k}$$としています。また、それぞれの着順をとった回数をまとめて$${\bm{N} = (N_1, N_2, N_3, N_4)}$$と表記することにします。あとで使います。
事前分布
次に、$${P(\bm{\theta})}$$について考えます。これは順位率$${\bm{\theta}}$$の事前分布と呼ばれていて、プレイヤーの試合結果$${\bm{X}}$$が与えられる前に、プレイヤーの順位率の分布がどんな感じだと想定しているかという事前の信念を表しています。たとえば、「プレイヤーの順位率がどうなるかは全然わからない」とか、「いくら強くても長期的には1位率40%は超えないでしょ」とか、そういう事前の信念を事前分布で表現できます。
事前分布には確率をいい感じに表現できて、カテゴリ分布とも相性がいいディリクレ分布を利用することにします。
$$
\newcommand{\paren}[1]{\left(#1\right)}
\newcommand{\one}[1]{\bm{1}\left\{#1\right\}}
\newcommand{\vX}{\bm{X}}
\newcommand{\vtheta}{\bm{\theta}}
\newcommand{\valpha}{\bm{\alpha}}
\newcommand{\Cat}{\mathrm{Categorical}}
\newcommand{\Dir}{\mathrm{Dirichlet}}
\newcommand{\sumi}{\sum_{i=1}^N}
\newcommand{\prodi}{\prod_{i=1}^N}
\newcommand{\prodk}{\prod_{k=1}^4}
\begin{align*}
P(\vtheta) &= \Dir\paren{\vtheta \mid \valpha} \\
&= \frac{1}{B(\valpha)}\prodk \theta_k^{\alpha_k - 1}
\end{align*}
$$
パラメータ$${\bm{\alpha}}$$を調整することで事前の信念を表現できます。なお、$${B(\bm{\alpha})}$$はベータ関数から計算されていますが、確率分布としての要件を満たすために積分したら1になるように調整しているだけなので、あまり気にしなくて大丈夫です。
「プレイヤーの順位率がどうなるかは全然わからない」ということを表現したい場合は、小さめの$${\bm{\alpha}}$$を設定します。$${(\alpha_1, \alpha_2, \alpha_3, \alpha_4) = (1, 1, 1, 1)}$$でもいいんですが、ディリクレ分布を無情報の事前分布として使いたいときは1/2を設定することがおすすめされています(参考:Jeffreys prior)。この場合、事前の順位率の分布は以下のようになると想定していることになります。

また、この場合の安定段位の分布は以下になります。

ただし、安定段位20以上はカットしています。事前分布が弱いということはどんな順位率もとり得ると想定していることを意味します。安定段位もどんな値にもなり得るという想定になるので、マイナスから20以上まで広がっています。
ただ、長期的に安定段位が11段を超えるとか、4位率が15%を切るというのは現実的には考えづらいです。そして、このような事前の信念を事前分布に反映してあげたほうが、より確からしい推定ができると考えることもできます。特に、プレイヤーの試合数が少ない場合、データから推定される順位率は信用性が低くなるので、事前の信念で調整してあげることが有効です。実際、たとえば$${(\alpha_1, \alpha_2, \alpha_3, \alpha_4) = (200, 200, 200, 200)}$$を設定してあげると順位率と安定段位の事前分布は以下のようになります。


順位率は25%を中心に20%から30%の間に、安定段位は7段を中心に5段から10段くらいの間に収まっています。データを受け取る前の信念として、こちらのほうがより妥当な想定をしているように見えます。実際、天鳳ランキングサイト(仮)から鳳南で2000戦以上打ったプレイヤーの安定段位お借りして、分布を可視化すると以下のようになっています。

実際の安定段位の分布は5.5段から10段くらいに分布していますが、事前分布の安定段位は5から10段くらいをカバーできているのでちょうど良さそうです。
ヒストグラムを見ると、安定段位がだいたい6.5段以下の人がガクッと少なくなっていますが、安定段位が低いと鳳凰卓から弾かれて打数が稼げない可能性が高くなることが影響していると考えられます。また、数千試合をこなす仮定で雀力が向上していることもありそうです。なので、この観測された安定段位の平均値は7.4段ですが、これは若干高めに出ていると思われます。そう考えると、事前分布の安定段位の平均が7段なことは悪くない設定だと思います。
もちろん、この事前の信念が正しい保証があるわけではないですし、パラメータをどのように決めるかによって推定結果が変わってくるという意味では分析者の恣意性が入ってきてしまいます。ただ、そもそもの話として、雀力は一定と仮定する、事前分布をディリクレ分布で表現する、などのモデリングにすでに分析者の意思が入っていることを考えると、事前分布のパラメータ設定だけをことさら取り上げるのも不自然とも考えられますし、主観がパラメータとして明示されている分むしろわかりやすいとも考えられます。ですので、この分析に限らず、分析には常に恣意性が入ってきていることに留意しながら、自分でより妥当だと思う設定に調整していってもらえたらと思います。
分母
最後に、$${P(\bm{X})}$$ですが、これは推定したいパラメータ$${\bm{\theta}}$$に関係なく、あとで積分して1になるように適当に調整すればOKなので無視します。
事後分布
以上の結果をまとめると、順位率の事後分布は以下のように表現できます。
$$
\newcommand{\paren}[1]{\left(#1\right)}
\newcommand{\one}[1]{\bm{1}\left\{#1\right\}}
\newcommand{\vX}{\bm{X}}
\newcommand{\vtheta}{\bm{\theta}}
\newcommand{\valpha}{\bm{\alpha}}
\newcommand{\Cat}{\mathrm{Categorical}}
\newcommand{\Dir}{\mathrm{Dirichlet}}
\newcommand{\sumi}{\sum_{i=1}^N}
\newcommand{\prodi}{\prod_{i=1}^N}
\newcommand{\prodk}{\prod_{k=1}^4}
\begin{align*}
P(\vtheta \mid \vX)
&= \frac{P(\vX \mid \vtheta)P(\vtheta)} {P(\vX)}\\
&\propto P(\vX \mid \vtheta)P(\vtheta)\\
&= \paren{ \prodk\theta_k^{N_k}}\paren{\frac{1}{B(\valpha)}\prodk \theta_k^{\alpha_k - 1}}\\
&\propto \prodk\theta_k^{\alpha_k + N_k - 1}
\end{align*}
$$
ここで、$${\propto}$$は比例関係を表します。繰り返しになりますが、推定したいパラメータ$${\bm{\theta}}$$に関係ない部分はあとで調整するので無視してOKです。実際、パラメータ部分に注目すると、これはパラメータ$${\bm{\alpha} + \bm{N}}$$のディリクレ分布と同じ形になっています。ということは、$${B(\bm{\alpha} + \bm{N})}$$で割ってあげれば積分して1になるよう補正でき、結局
$$
\newcommand{\paren}[1]{\left(#1\right)}
\newcommand{\one}[1]{\bm{1}\left\{#1\right\}}
\newcommand{\vX}{\bm{X}}
\newcommand{\vN}{\bm{N}}
\newcommand{\vtheta}{\bm{\theta}}
\newcommand{\valpha}{\bm{\alpha}}
\newcommand{\Cat}{\mathrm{Categorical}}
\newcommand{\Dir}{\mathrm{Dirichlet}}
\newcommand{\sumi}{\sum_{i=1}^N}
\newcommand{\prodi}{\prod_{i=1}^N}
\newcommand{\prodk}{\prod_{k=1}^4}
\begin{align*}
P(\vtheta \mid \vX)
&= \frac{1}{B(\valpha + \vN)}\prodk\theta_k^{\alpha_k + N_k - 1}\\
&=\Dir\paren{\vtheta \mid \valpha + \vN}
\end{align*}
$$
となります。つまり、順位率$${\bm{\theta}}$$の事後分布はパラメータ$${\bm{\alpha} + \bm{N}}$$のディリクレ分布に従います。このように、事後分布が事前分布と同じ分布族になるような事前分布のことを共役事前分布と呼びます。共役事前分布を用いると事後分布を解析的に求められるので便利です。
事後分布のパラメータを確認すると、順位率$${\bm{\theta}}$$の事後分布は事前分布のパラメータ$${\bm{\alpha}}$$と戦績$${\bm{N}}$$のあわせ技で決まりまることがわかります。事前の信念が弱いと($${\bm{\alpha}}$$が小さいと)データを強く信頼した推定を行いますし、一方で事前の信念が強いと($${\bm{\alpha}}$$が大きいと)データだけでなく事前の信念も考慮して推定を行うことになります。
モンテカルロシミュレーションによる事後分布の近似
事後分布の形は解析的に求まりましたが、ここから安定段位の事後分布を計算したり、プレイヤー1とプレイヤー2の安定段位の事後分布を比較してプレイヤー1が強い確率を算出したりするのは大変です。なので、モンテカルロシミュレーションで近似することにします。事後分布の形状はわかっているので、ここから$${M}$$個の順位率$${\bm{\theta}}$$をサンプリングします。
$$
\newcommand{\paren}[1]{\left(#1\right)}
\newcommand{\one}[1]{\bm{1}\left\{#1\right\}}
\newcommand{\vX}{\bm{X}}
\newcommand{\vN}{\bm{N}}
\newcommand{\vtheta}{\bm{\theta}}
\newcommand{\valpha}{\bm{\alpha}}
\newcommand{\Cat}{\mathrm{Categorical}}
\newcommand{\Dir}{\mathrm{Dirichlet}}
\newcommand{\sumi}{\sum_{i=1}^N}
\newcommand{\prodi}{\prod_{i=1}^N}
\newcommand{\prodk}{\prod_{k=1}^4}
\begin{align*}
\vtheta^{(m)} \sim \Dir\paren{\vtheta \mid \valpha + \vN}
\end{align*}
$$
これを使うと安定段位を$${M}$$個求めることができます。
$$
\newcommand{\paren}[1]{\left(#1\right)}
\newcommand{\one}[1]{\bm{1}\left\{#1\right\}}
\newcommand{\vX}{\bm{X}}
\newcommand{\vN}{\bm{N}}
\newcommand{\vtheta}{\bm{\theta}}
\newcommand{\valpha}{\bm{\alpha}}
\newcommand{\Cat}{\mathrm{Categorical}}
\newcommand{\Dir}{\mathrm{Dirichlet}}
\newcommand{\sumi}{\sum_{i=1}^N}
\newcommand{\prodi}{\prod_{i=1}^N}
\newcommand{\prodk}{\prod_{k=1}^4}
\begin{align*}
安定段位^{(m)} = \frac{1}{15}\paren{\frac{90\theta_1^{(m)} + 45\theta_2^{(m)}}{\theta_4^{(m)}} - 135}
\end{align*}
$$
この操作をプレイヤー1とプレイヤー2でそれぞれ行い、プレイヤー1の安定段位がプレイヤー2の安定段位よりも高かった割合を求めることで、プレイヤー1のほうが(安定段位の意味で)強い確率を求めることができます。
$$
\newcommand{\paren}[1]{\left(#1\right)}
\newcommand{\one}[1]{\bm{1}\left\{#1\right\}}
\newcommand{\vX}{\bm{X}}
\newcommand{\vN}{\bm{N}}
\newcommand{\vtheta}{\bm{\theta}}
\newcommand{\valpha}{\bm{\alpha}}
\newcommand{\Cat}{\mathrm{Categorical}}
\newcommand{\Dir}{\mathrm{Dirichlet}}
\newcommand{\sumi}{\sum_{i=1}^N}
\newcommand{\prodi}{\prod_{i=1}^N}
\newcommand{\prodk}{\prod_{k=1}^4}
\begin{align*}
P\paren{安定段位_1 > 安定段位_2} \approx \frac{1}{M}\sum_{m=1}^M\one{安定段位_1^{(m)} > 安定段位_2^{(m)}}
\end{align*}
$$
シミュレーション
実際にモンテカルロシミュレーションで事後分布を近似してみましょう。具体的に、以下の2名のプレイヤーの安定段位を比較することにします。
プレイヤー1:500戦で順位率が$${(0.29, 0.26, 0.23, 0.21)}$$の安定段位10段
プレイヤー2:3000戦で順位率が$${(0.27, 0.26, 0.25, 0.22)}$$の安定段位8.9段
事前分布のパラメータが1/2の場合
まずは、弱い事前分布を置いた場合、つまり、プレイヤーの順位率に対して事前には何もわからないと考えている場合についてシミュレーションします。具体的に$${(\alpha_1, \alpha_2, \alpha_3, \alpha_4) = (1/2, 1/2, 1/2, 1/2)}$$のケースを考えると、プレイヤー1の順位率の事後分布は以下のように推定されます。

事後分布から順位率を10万回サンプリングしてヒストグラムとして可視化しました。プレイヤー1のトップ率は29%だったので、それが最頻値となっています。とはいえ500試合の結果だと不確実性があるので、確実に29%と推定されるわけではなく、不確実性が考慮されています。この順位率の分布から計算された安定段位の事後分布は以下になります。

プレイヤー1は10段の確率が高いが、500戦の結果なので不確実性も大きくでていることが見て取れます。現実的には考えづらいですが、12段や13段の可能性も十分にあるこという推定になっています。
同様に、プレイヤー2の順位率と安定段位の事後分布を見ます。


だいたい9段を中心に分布していることがわかります。
それでは、いよいよプレイヤー1とプレイヤー2の安定段位を比較します。画像がバラバラだとプレイヤー1とプレイヤー2の比較がしづらいので、安定段位の画像を重ねてみましょう(画像左)。
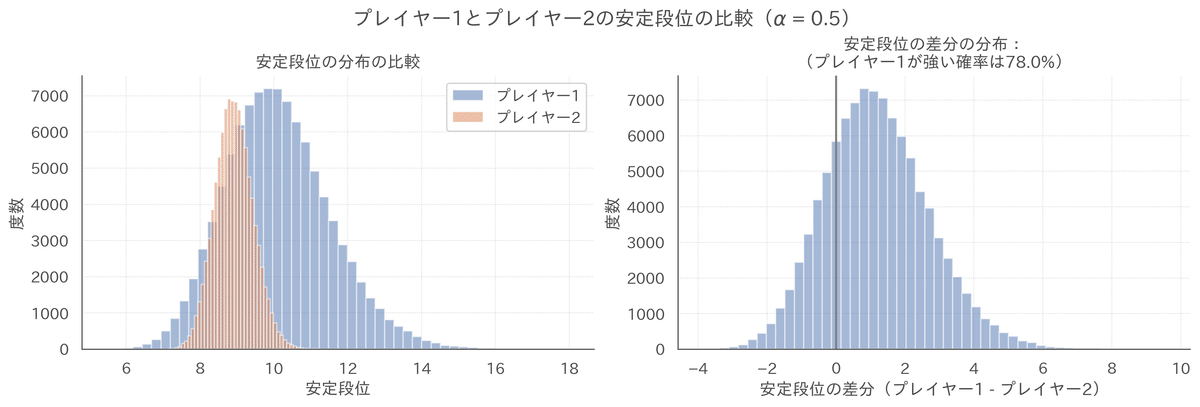
プレイヤー1の事後分布と比較して、プレイヤー2の事後分布は圧倒的に狭い区間に分布していることがみてとれます。プレイヤー1の安定段位は500戦の結果から計算されていますが、プレイヤー2の安定段位は3000戦の結果から計算されており、信頼度がかなり高まっています。
両プレイヤーの分布を比較すると、プレイヤー1の方が安定段位が高い可能性が高そうです。実際、安定段位の差分をとって可視化すると右図のようになります。差分が0以上の部分をカウントすると、プレイヤー1が強い確率が78%となりました。
事前分布のパラメータが200の場合
弱い事前分布を置いた場合はプレイヤー1が強い確率が高くなりました。しかし、安定段位の事後分布を確認すると、現実的に考えてその可能性は低いにもかかわらず、プレイヤー1の安定段位が10を超える可能性がかなり高く推定されてしまっています。
前述したように、鳳南2000戦以上打っているプレイヤーの安定段位の分布を知っています。その知識を使えば「何もわからない」よりも妥当な事前分布を考えることができそうです。実際に、事前分布のパラメータを$${(\alpha_1, \alpha_2, \alpha_3, \alpha_4) = (200, 200, 200, 200)}$$とするプレイヤー1の順位率と安定段位の事後分布は以下になります。
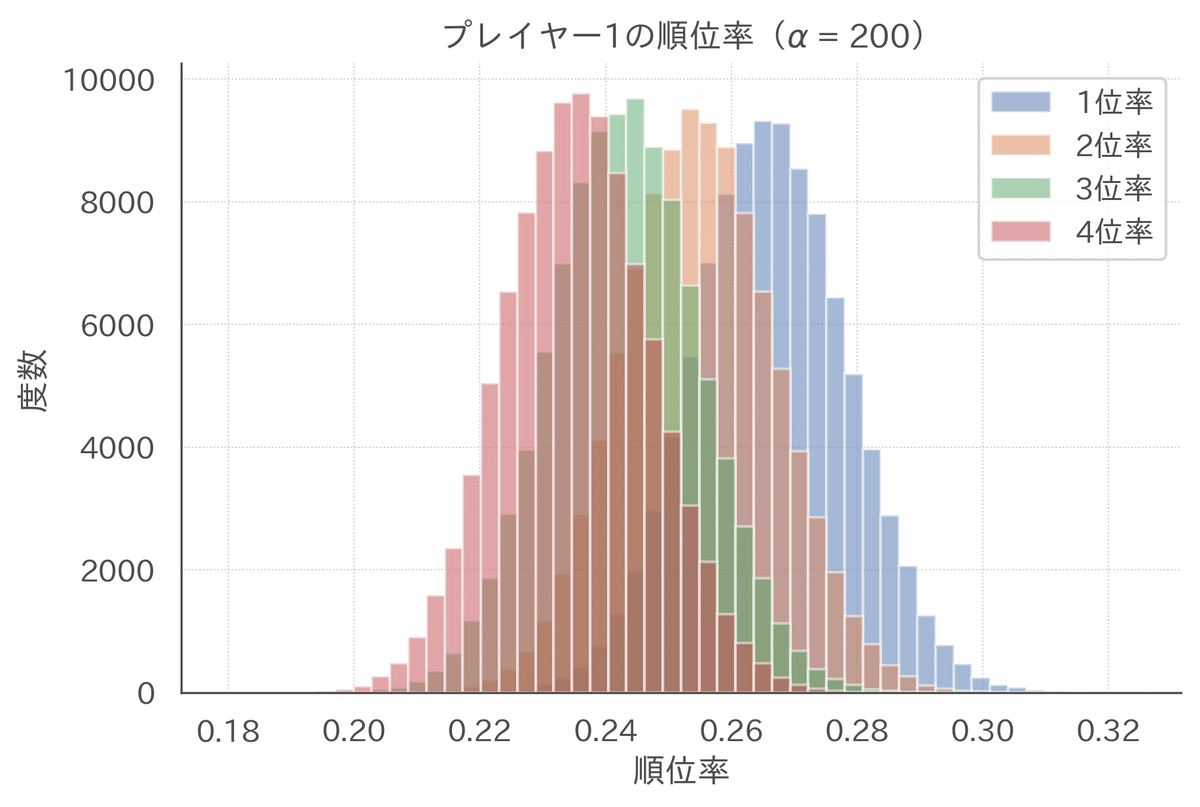

500戦の結果だけをみると安定段位は10段ですが、試合数が少ないので事前分布に強く引っ張られて「実際は8.5段くらいと想定するのが妥当でしょ」という推定になっています。
同様に、プレイヤー2の事後分布は以下になります。


試合数が多いのでプレイヤー2は相対的に事前分布の影響を受けづらく、安定段位の最頻値も8段くらいに落ち着いています。
プレイヤー1とプレイヤー2の安定段位の事後分布を比較したものが以下になります。

先程とは打って変わって、プレイヤー2の事後分布のほうが右側によっていることが見て取れます。実際、安定段位の差分を取るとプレイヤー1が強い確率は30.3となり、プレイヤー2のほうが強い可能性が高いことがわかります。
弱い事前分布と強い事前分布で逆の結果になりました。どちらの結果を信用するかですが、僕は強い事前分布の結果のほうがより妥当、より現実的だと思います。せっかく他のプレイヤーの戦歴から安定段位の分布に関する情報がわかるので、使える情報は使ったほうが妥当な分析になると思うからです。これは僕がそう思っているだけなので、実際に使う場合は納得の行く方を使ってみてもらえればと思います。
まとめ
この記事では、ベイズ推定を利用して安定段位の事後分布を推定する方法と、プレイヤー間で安定段位の比較方法を検討しました。ベイズ推定は事前分布の設定で結果が変わる場合があるので、実際に利用する際には自分が納得の行くやり方で計算してもらえればと思います。
例によって、この記事は間違いを含んでいる可能性もありますし、より良いやり方がある可能性もあります。間違いのご指摘やご意見などあれば、ぜひTwitter(@ippou1000)などでご連絡いただけると嬉しいです。
コード
可視化のコードがほとんどで、コアのコードはこれだけです。
事前分布のパラメータalpha、順位率p、試合数n_roundsを指定してあげれば、事後分布からn_draws回順位率をサンプリングしてくれる関数です。ついでに平均順位や安定段位も計算してくれます。
def draw_posterior(
alpha: np.ndarray = np.ones(4) / 2,
p: np.ndarray = np.array([0.25] * 4),
n_rounds: int = 0,
n_draws: int = 100000,
) -> pd.DataFrame:
df = pd.DataFrame(
np.random.dirichlet(alpha + p * n_rounds, size=n_draws),
columns=["1位率", "2位率", "3位率", "4位率"],
)
df["平均順位"] = df.values @ np.array([1, 2, 3, 4])
df["安定段位"] = 7 + ((90 * df["1位率"] + 45 * df["2位率"]) / df["4位率"] - 135) / 15
return df