
数理盤の成り立ち

数理盤の成り立ちをプラトン図形を使って説明したいと思います。
私達人間は三次元的存在ですから、三次元を認識するためには4次元以上の存在でないと認識できないというのはいいですね。
では、私達の一生の人生空間を正六面体で表現し、上下を省いた側面を映画のスクリーンのように見立てて、映し出される考えてみましょう。
4つの側面が人生の春、夏、秋、冬として映し出されるのです。
それを四次元方向からみつめているわけです。もちろんスクリーンに落ち込んでいる私達にはそのことは分かりません。
そうするとこのモデルで4次元方向って、どこにあたるのでしょうか?
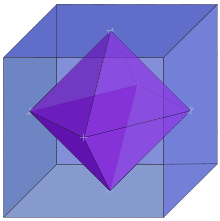
なお、この正六面体の中に入っているのは正八面体は肉体空間です。もちろん一生における肉体空間です。
この空間は螺旋運動をしていると考えてみましょう。もちろん三次元的存在である私達にはそれはわかりません。
そうすると、回転しているうちに六角形の形に見える視覚が現れる事が分かります。

この正六面体が六角形の形になったときに、四次元方向が現れるというのはよろしいですね。


この正六面体が六角形になったとき、つまり、正六面体の立体対角線が一点になるとき、四次元方向の視点が開かれます。
この立体対角線が一点になるときですね。
こんな形です。


そうすると、立体対角線が中心の一点になるとき、正八面体の中心から角が出て(動画のオムニスターのように)正六面体の面の一点に出ます。これが現象であります。正六面体の立体対角線から、正八面体の禄方向軸に変換されます。つまり四次元が三次元に変換された事を示します。

六方向の面に接するのですが、どれか一点において現象になります。

この一点はホログラムのように部分は全体を含むごとく四次元視点の表裏を含んだ構造になっているということです。(何故、表裏を含むかはこれから説明しますね。)
四次元視覚ではどうなっていたかと申しますとこちらから見ると六角形です。ただし、こちらから見た図だけでは現象になりませんから、かならず反対側から見みる必要があります。
反対側から見ると、正三角形八面体が外に出て、正四角形六面体が内側に入る形になります。形としては六角形ですが、反対方向から見ますと、反転しますので縦が横になります。
ちょうど野球のボールのようになります。




これを縦亀甲と横亀甲と言います。
これを直行させたもの(両方同時に見た図)が私達が使っている数理盤です。

なんとなく分かったような気になりますが、まだ腑に落ちないと思います。
ではこの意味を立体的で考えてみましょう。

四次元方向の視点が現れるのは正六面体の頂角でした。そして正八面体の六軸方向が三次元空間を作る方向でした。
まず正六面体の頂角に接する外接球を作ります。それは四次元空間を現す球体です。そして正六面体の内接球を作ります。こちらは三次元を現す球体です。

左が四次元を現す球体。右が三次元を現す球体。
四次元からの視点は六面体が六角形になったときですから、この場合立体対角線は距離がなくなりますから、四次元球から三次元球に射影すると考えても良いわけです。そうすると三次元の球体は四次元の球から射影されますから二重の空間をもつことになります。
ただし、この場合、射影されるのは立体対角線を通じてですから、4つの立体対角線の軸の球体を作らなくてはいけません。そして三次元球面に射影するわけですから、軸の長さは正八面体の軸の長さにしなければいけません。
それを表現したのが、ベクトル平衡体がつくる14面体球です。これは三次元球体の半径(つまり正八面体の軸の長さ)でカットしたモデルです。
これを高速回転させると球体になります。
この14面体モデルは正六面体と正八面体の両方を等化した一つ上の次元のモデルになります。

これを回転させるともう一つの亀甲(六角形)があらわれます。
さらに回転させると両方を含んだ図形が現れます。

これは、縦亀甲と横亀甲の両方を含んでいます。四隅を重なっていいると見ると全部で9つの場。重なっていないと見ると12の場になります。
縦の亀甲と横の亀甲が現れますね。
動画をみて参考にしてください。
私達が使っている数理盤は4次元を投影したものだということを頭に入れておいて下さい。
これを時間空間論で考えると四次元の視覚という部分を局所場である空間場が一転して時間波(場)に変換されると言い換えれば良いです。
