ソートアルゴリズム「ヒープソート」とは？

「ヒープソート」。

IPAの基本情報試験や応用情報試験を勉強していると、必ずといっていいほど目にするソート名ですが、実際にどのようなソートがなされているのかご存じでしょうか。

今回は、ヒープソートについての概要、実際にどのようにソートが行われるのか、について紹介していきたいと思います。

ヒープソートとは

ヒープソートとは。Wikipediaによると、

「リストの並べ替えを二分ヒープ木を用いて行うソートのアルゴリズムである」

らしいです。よく分からないですね。

ヒープソートの手順について、またまたWikipediaによると、

１. 未整列のリストから要素を取り出し、順にヒープに追加する。すべての要素を追加するまで繰り返し。

２ . 根（最大値または最小値)を取り出し、整列済みリストに追加する。すべての要素を取り出すまで繰り返し。

少し分かってきたでしょうか。自分は怪しいです。

そもそも、「ヒープ」とは、どのようなものでしょうか。

一言でいうならば、

「親要素が子要素よりも常に大きい（もしくは小さい）値をもつデータ構造」

のことです。

例として、以下のように、根（ヒープの一番上の要素）に最大値が入っているもの（以降、図1という）として考えていきたいと思います。

まずは一番上の要素である「10」から見ていきましょう。

「10」は「根」であると同時に「親」でもあります。そして、親である「10」の「子」にあたる要素は、「8」,「9」となります。

同様に考えていくと、親である「8」と「9」の「子」にあたる要素は、それぞれ「4」,「7」と「1」,「6」になります。

このように、「ヒープ」とは「親要素 > 子要素」の関係を常にもつデータ構造であることを意識しましょう。

ヒープソートの流れ

ヒープについて把握できたところで、ヒープソートの流れを紹介していきたいと思います。

大まかな手順としては、

１. ヒープの根から最大値を取り出し、これを別に用意した配列の末尾に置く。

２. 根を失ったヒープを再構成し、１の手順を行う。以降、配列が埋まるまで繰り返す。

といった具合です。

上記の手順、図1と照らし合わせてみると、まずは根である「10」を配列の末尾に入れることになります。配列については、上の行には「要素番号」、下の行には「値」が入るものとします。

すると、ヒープから根であった「10」が消えてしまい、ヒープの定義を満たさなくなるので、再構成していく必要が生じます。

根が除かれたヒープでは、一番下の要素を根に持ってきます。上図の場合、「5」を根に持っていきます。

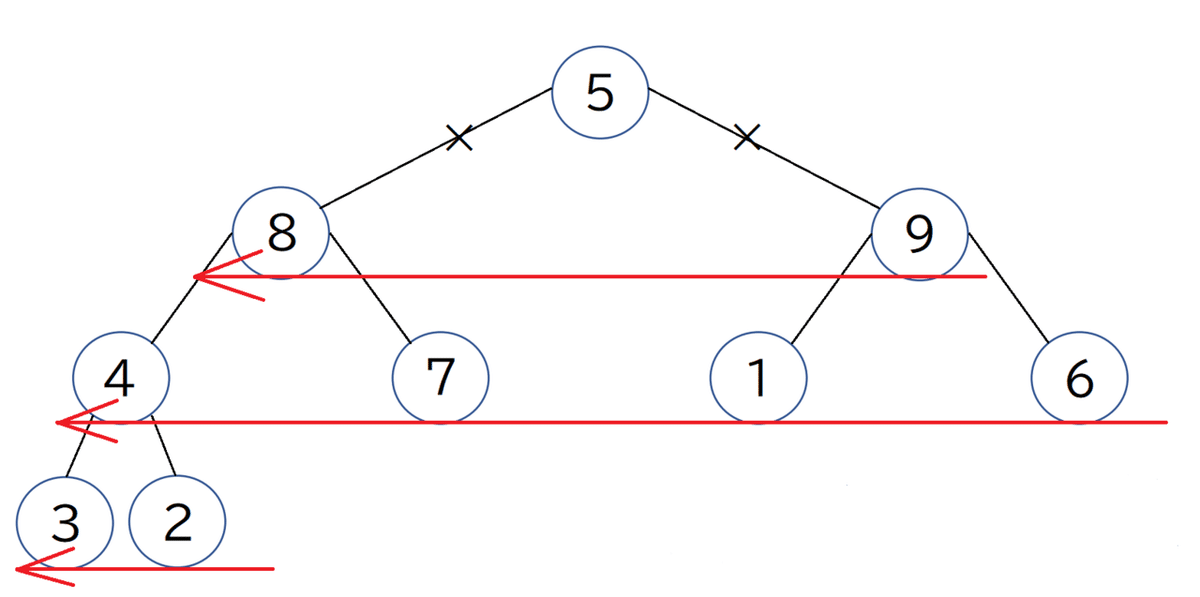
「5」を根にすると、その子である「8」,「9」との親子関係（親 > 子）がとれていないことが確認できます。このような場合は、一番下の要素の右から左へ、そして、その上の要素の右から左へ見ていき、上の親との関係が正しいかを確認していきます。上図の場合、順を追って見ていくと、根(5) > 子(9) の関係を満たしていないことが分かるので、これらを入れ替えます。

再度、順を追って見ていくと、親(5) > 子(6) の関係を満たしていないことが確認できるので、これらを入れ替えます。

これで、ヒープの定義を満たした構造に再構築することができたので、配列に根である「9」を格納します。

以降、先ほどと同様にヒープの再構築を行い、根を配列に格納し…という作業を繰り返すことでソート処理を行います。

ヒープソートの流れについて、理解したところで、実際にトレース（数値を当てはめてアルゴリズムの処理を順に行っていくこと）を行いたいところですが、分量が多くなりそうなので、今回は一旦このあたりで区切りたいと思います。

余裕のある方は、以下の記事を参考に実際にトレースを行ってみてください。

https://note.com/inc_daifuku/n/nd94135fcfd6e

著者：かわ