
ふんわり統計学 -仮説検定の仕組み-
こんにちは!事業会社でデザイナーをしているhukuroです。
広告の集客率や、ランディングページのCVR(コンバージョン率)等を改善するために行われるA/Bテスト。
A/Bテストツールが示す勝ち負け判定に従い「成果が良い」とされたクリエイティブを採用したが、効果が現れてこないという経験ありませんか?
A/Bテストをしていつも気になるのは、「どのくらいのサンプル数のテストを実施したら統計学的に決着がついたといえるのか」です。果たしてあのテストは本当に決着がついていたのでしょうか…
ツールが示す判定が本当に正しいのかどうかが気になり調べてみた結果、統計学の「仮説検定」という概念に行き当たりました。
この記事は、私と同じような「統計学初心者だけど普段のサービス改善業務で何気なくこの領域に触れてる人」に向けて、簡単に仕組みなどをまとめてみたものになります。色々と省いたり分かりやすい言葉にしながら説明をしていますが、間違いがありましたらご指摘ください!
目次
・仮説検定ってどういうもの?
・「LPでA/Bテストを実施した場合」を例に考える
・手順① 期待する結果を考える
・手順② 対立仮説/帰無仮説の設定
・手順③ 有意水準を決める
・手順④ 実データで判断する
・「有意差あり」の状態になるには?
・まとめ
仮説検定ってどういうもの?
仮説検定の考え方では、ある立証したい仮説に対し、「敢えて反対の仮説の立証を試みて、確率的にありえない事が起きた!という事実から棄却し、反対の(元々立証したかった方の)仮説を採択する」といった、回りくどい方法をとります。(背理法の考え方ですね!)

考え方がやや複雑なため、実際の例で考えてみましょう。
「LPでA/Bテストを実施した場合」を例に考える
とあるWebサイトのLPで、CVR向上を狙った新しい機能の追加を検討しており、テストマーケティング(A/Bテスト)を実施することになりました。
(a)既存パターン:現行サイトから変更無しの状態
(b)新規パターン:新機能を追加した状態
※それぞれのパターンに「ランダム」に「同等数のユーザー」が振り分けられるものとする。
上記2パターンのCVRを比較し、成果の良い方を採用したい。
この例で仮説検定を利用してはっきりさせたいのは、「どちらのCVRが高いか」という勝敗の決着がついたかどうかになります。
このとき、仮説検証は以下のような手順で行っていきます。
手順① 期待する結果を考える

まずは期待している結果を考えます。
ここでは勝ち負けどちらにせよ、ユーザーに何らかの行動の変化があると考えているため、期待している結果は「既存パターンと新規パターンのCVRは異なる状態(勝敗の決着がついた状態)」となります。
手順② 対立仮説/帰無仮説の設定
以下2つの仮説を立てます。
対立仮説:主張したい(期待する)仮説
帰無仮説:棄却したい(否定したい)仮説
対立仮説には期待する仮説を置き、帰無仮説には否定したい仮説(反対の仮説)を置きます。

既存パターンのCVRをA、新規パターンのCVRをBとすると
対立仮説:A ≠ B
帰無仮説:A=B ←否定したい
帰無仮説とは、無に帰す、つまり「最初からダメになることを狙って検証する仮説」ということになります。これからこの帰無仮説を間違っていると判断(棄却)させ、対立仮説を採択するという流れになります。
手順③ 有意水準を決める
有意水準とは、「この確率を下回っていたら"稀なこと"として帰無仮説を棄却する」という決めの確率です。
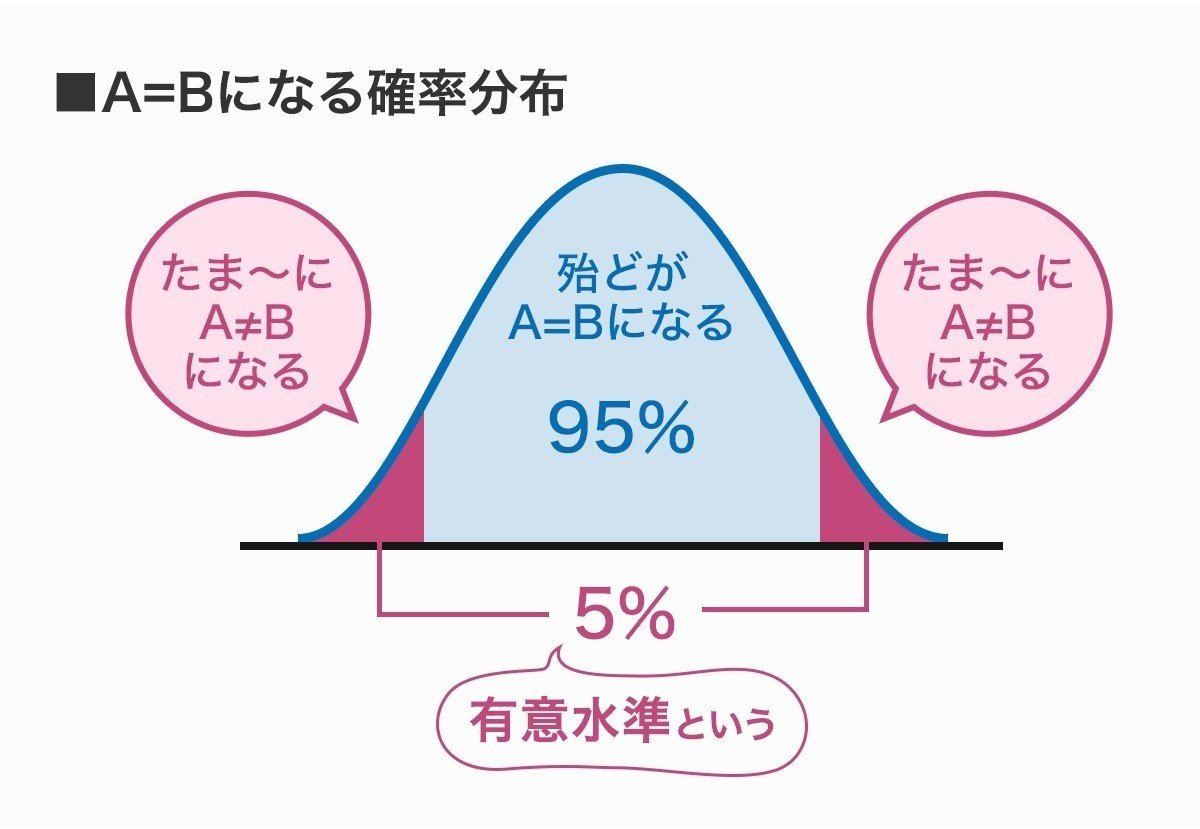
統計学の中で一般的には5%や1%で設定されることが多いようですが、この数値には数学的な裏付けは無いそうです。
手順④ 実データで判断する
帰無仮説が正しいと仮定した場合に期待される【検定統計量の確率分布】において、実データから得られた確率が有意水準より小さいかどうかで、帰無仮説を棄却するかどうかが決まります。

「有意差あり」の状態になるには?
では「有意差あり」の勝敗の決着がついた状態になるには、何がどうなっていれば良いのでしょうか。
判定に影響する2つの要素をみていきましょう。
①既存パターンと新規パターンのCVRの差
既存パターンと新規パターンのCVRの差が大きい場合、
【帰無仮説:A=B】の可能性が低くなるため有意差は出やすくなります。
②テストを実施したユーザの数(テスト母数)
テスト母数が多いほど、AとBそれぞれのCVRのばらつきが無くなり
【帰無仮説:A=B】の可能性が低くなるため有意差は出やすくなります。
まとめ
A/Bテストにおいて、統計学的に誤差が生まれにくい判断をするためには、
①CVRが大きく変化するテストを行う
②テスト対象のユーザー数を多くする
これらに取り組む必要があります。
あまり実用的では内容になりましたが、如何でしたでしょうか。
私は推測統計学を学んでみて、推測統計学的な判断では確率を利用するため、常に5%(1%)の割合で判定が誤る危険性が孕んでいるということを知りました。
100%理解することは難しかったのですが、理屈を知っておくことでツールの判断を鵜呑みにせず考えて結論を出すことが出来そうです。
