
【機械学習】PaCMAPで高次元を見る【次元削減】
最近、次元削減の手法について整理してたので、今回はPaCMAPの紹介をしてみます。
改めて勉強してたら、次元削減おもろ!!あたまよ!!かっこよ!!!ってなったので少しでも共有できたら嬉しいです☺️
お品書きはこんな感じです。
イントロ
次元削減とは高次元データの様子を低次元データに変換し、扱いやすくするための手法群です。
たぶん主成分分析が一番有名ですね。他にもt-SNE,UMAPなども有名かなと思います。
今回紹介するPaCMAPもこのような次元削減の手法の一つです。
低次元として2次元を選ぶと、変換結果の散布図をかくことができます。他の手法と比較しつつPaCMAPによる次元削減の凄さを散布図をたくさんかいて眺めてみましょう。
いい感じの次元削減とは?🤔
いい感じの次元削減手法を作るためには、どう振る舞っていればいい感じなのかを胸に手を当てて考える必要があります。
この記事ではたくさん実験をしてみたいので、実際にPaCMAPを実行して振る舞いを見てみましょう。比較のためにMDS(多次元尺度構成法)、UMAPでも実行してみます。
localな構造を保つ
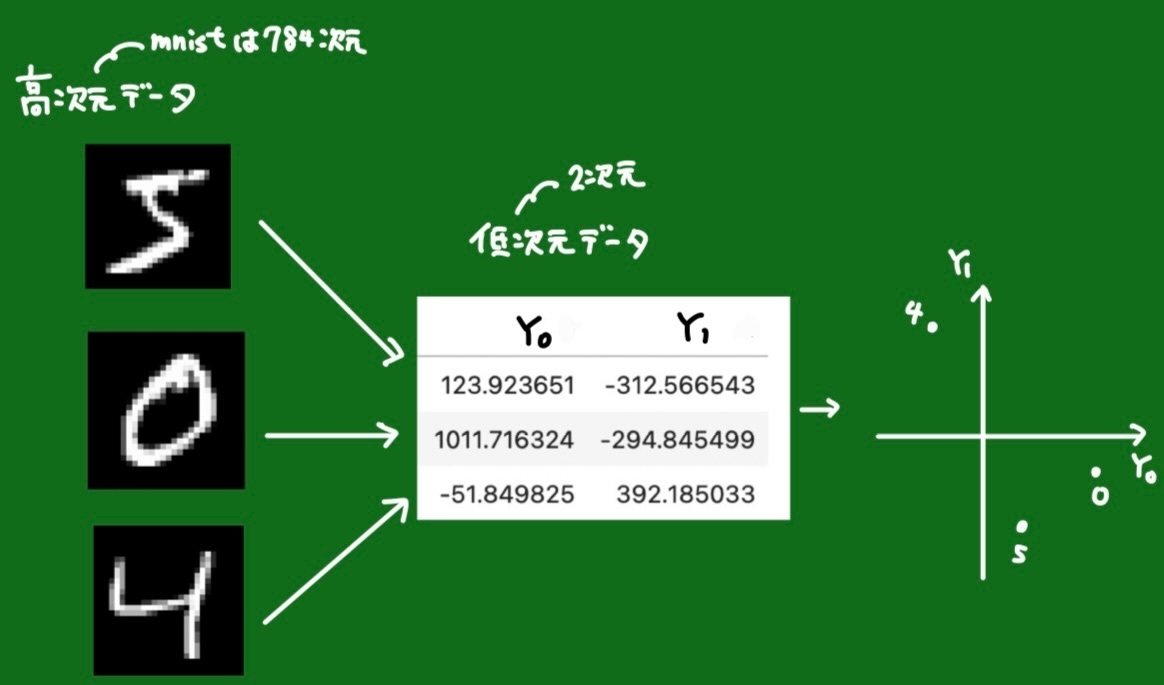
使うデータはみんな大好きmnistデータです。縦横28のピクセルを持つ画像のデータで0から9までの数字が手書きで書かれています。
784(=28×28)次元のデータをそれぞれの手法で2次元に変換し、結果をプロットしてみます。
MDSの結果を見てみましょう。mnist全部で実行しようとしたら時間がかかりすぎたのでサイズを落としています。
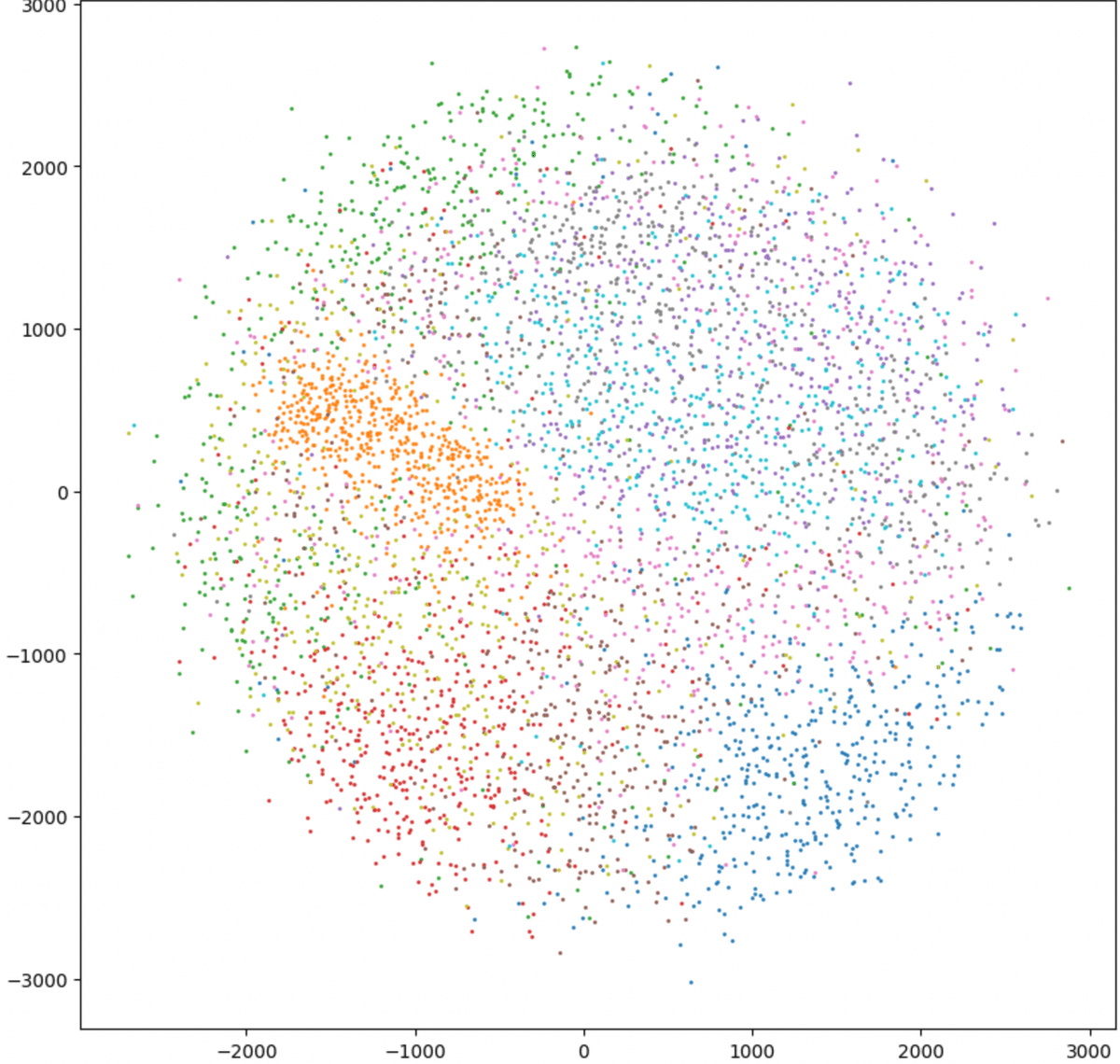
プロットの各点はデータ点(つまり今回は1枚の手書き画像)に対応しています。また、点の色は正解ラベルに対応しています。
mnistデータは然るべきモデルで学習すれば高精度でラベルの分類ができます。ということは、784次元空間の中で(想像するのは難しいけど)各ラベルはある程度分離して存在しているはずです。
このことを踏まえて、MDSのプロットを見てみましょう。
同じ色ごとには結構固まっていますが、各かたまりが重なり合ってぐちゃっとなっています。「元の高次元では分離している」という大事な情報が見えなくなってしまっていますね😩(このような現象をcrowding problemといいます)
対して、UMAPはこんな感じ
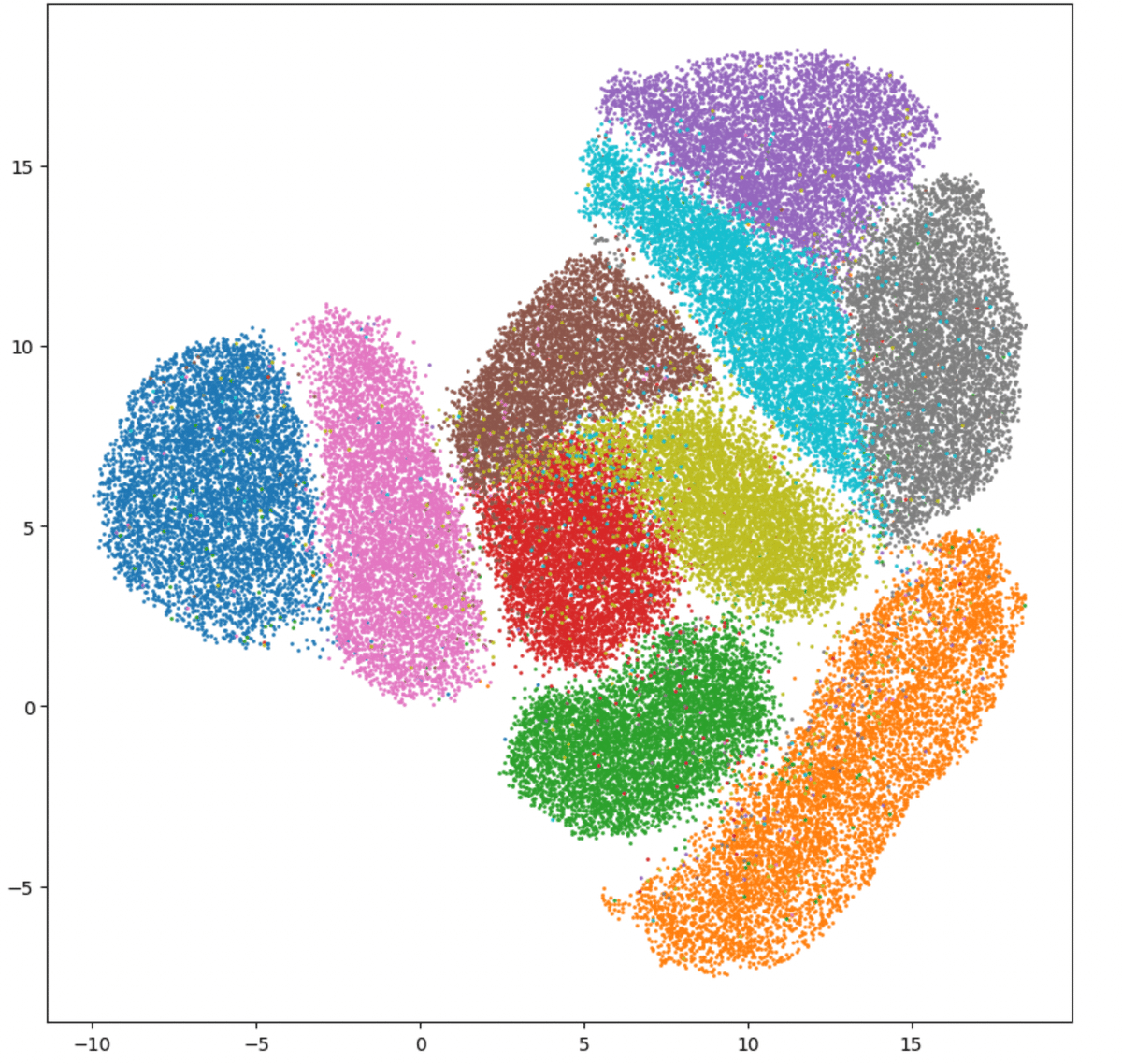
そして本命のPaCMAPはこう
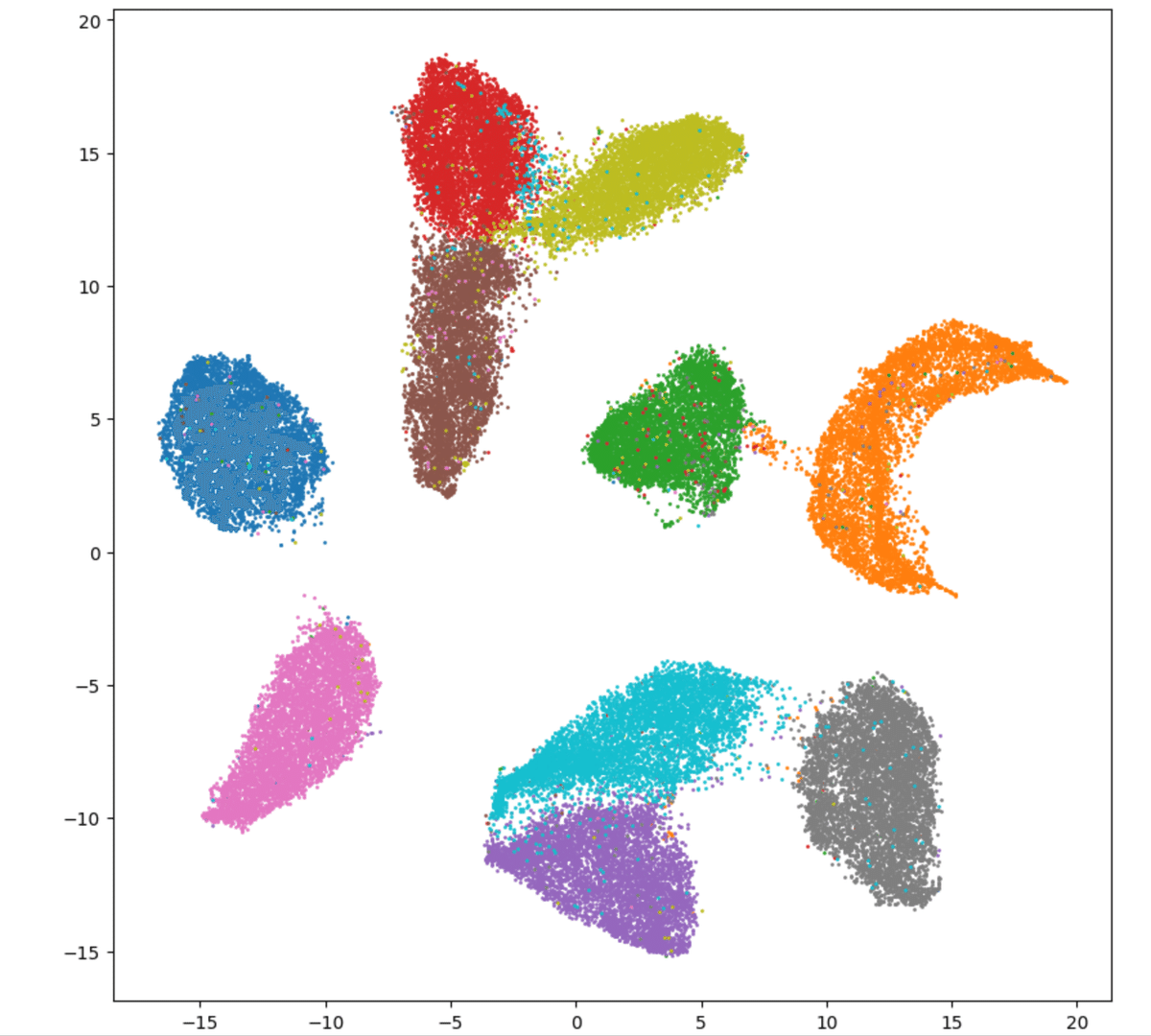
MDSと違ってUMAPとPaCMAPでは各かたまりがはっきり分かれているのが見て取れます。
UMAPとPaCMAPではこの分離みがちゃんと保存されているのが、いい感じポイントの1つめです。
分離したかたまり(つまりクラスター)の有無についての構造をlocalな構造といいます。
globalな構造を保つ
これだけだとUMAPとPaCMAPの違いが見えてきていないので、別のデータでも見てみます。
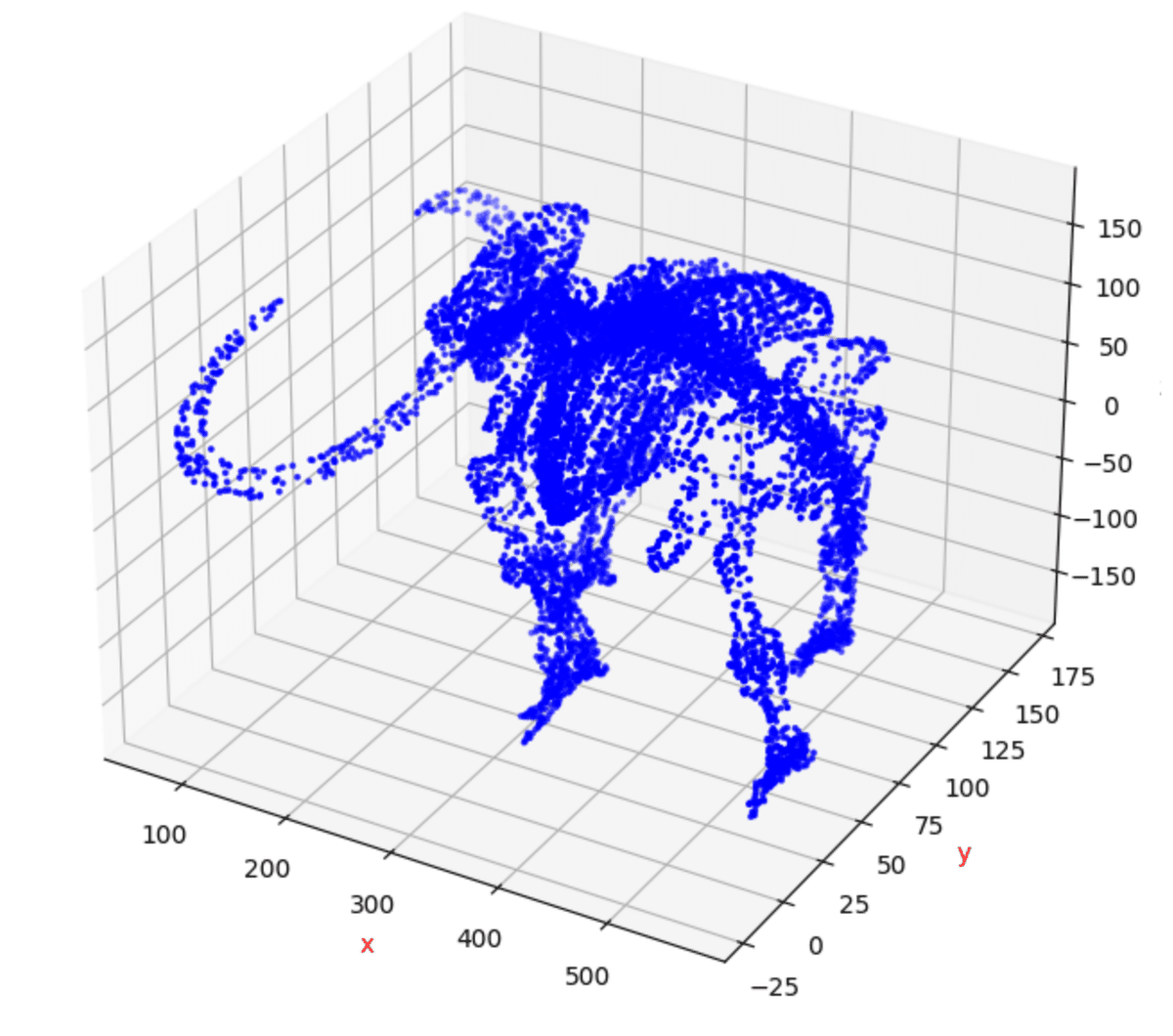
使うのはmammothデータです。これは、マンモスの骨格に沿って点が散布している3次元のデータです。胴体から牙や脚、尻尾などが生えています。
3次元なので次元削減タスクの対象としては微妙ですが、様子がわかりやすいのでこれでやってみます。
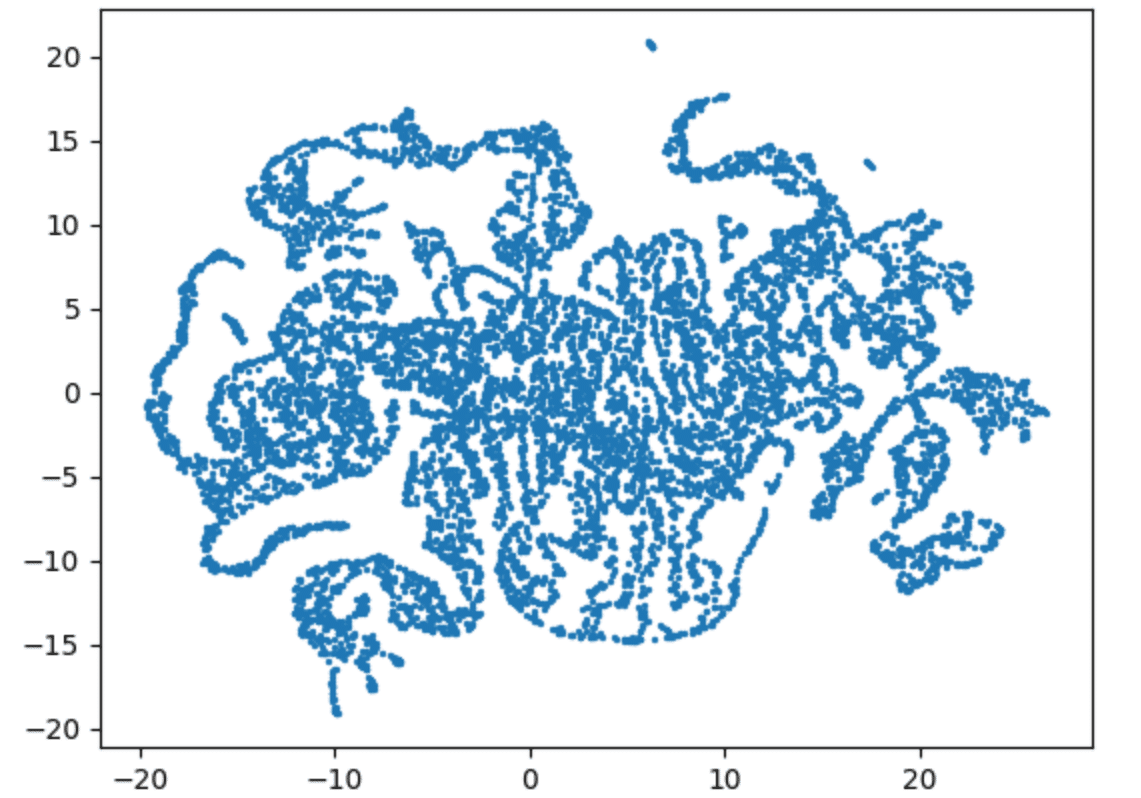
UMAPでの実行結果はこうです。
PacMAPではこんなふうになります。だいぶマンモスみありません?
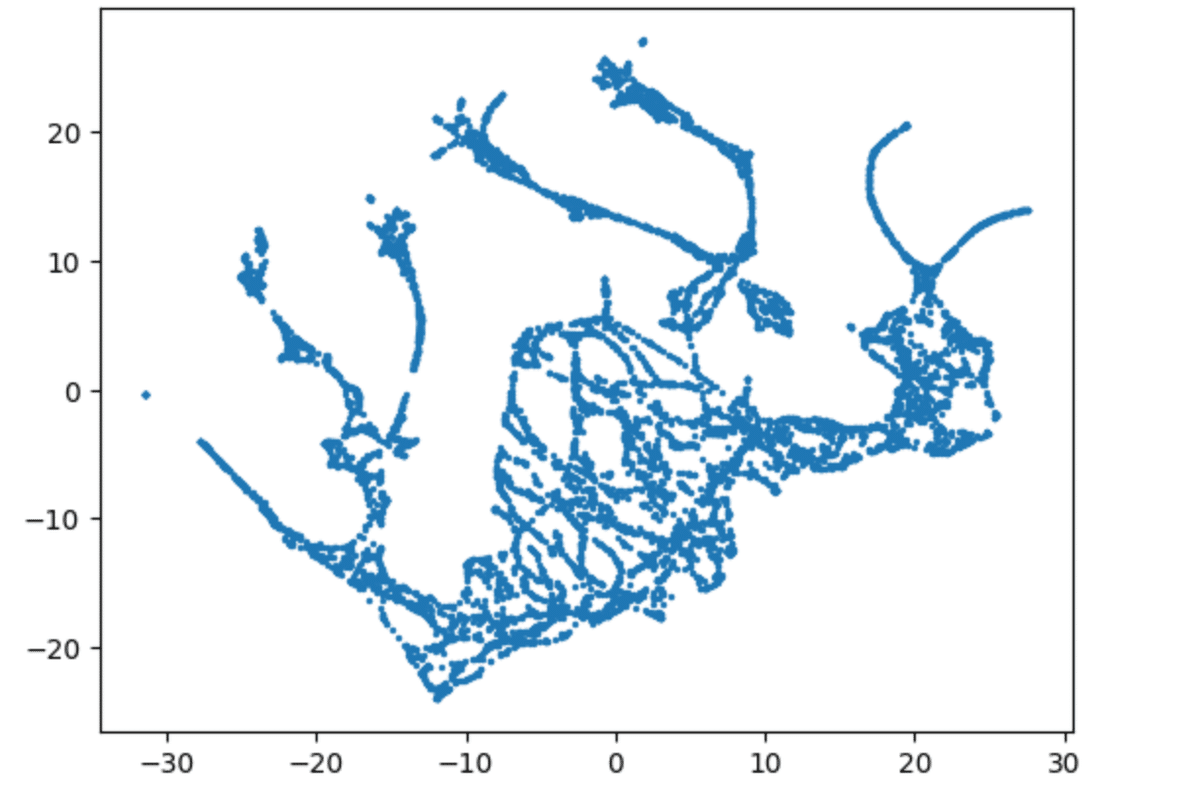
PaCMAPの方が胴体にあたるかたまりから牙や脚が細く伸びている感じが保たれている感じがよく出てるように見えます。牙がくるんってなってるのも少し表現できていそうです。
点同士の相対的な位置関係についての構造をglobalな構造といいます。
localな構造、globalな構造を共によく保ってくれそうな手法がPaCMAPです。
もっと実験してみる
globalな構造というのが抽象的でわかりにくいと思うので別の例でも見てみます。点の並びの曲がり具合はglobalな構造の要素です。
そこで、曲がり具合がないような点の並び、つまり直線的に並んだ点に対して次元削減をおこなってみます。
用意したのは10次元のデータで、原点で直交する2本の直線に沿って点を配置しています。
このデータをUMAPで2次元に次元削減した散布図がこちらです。
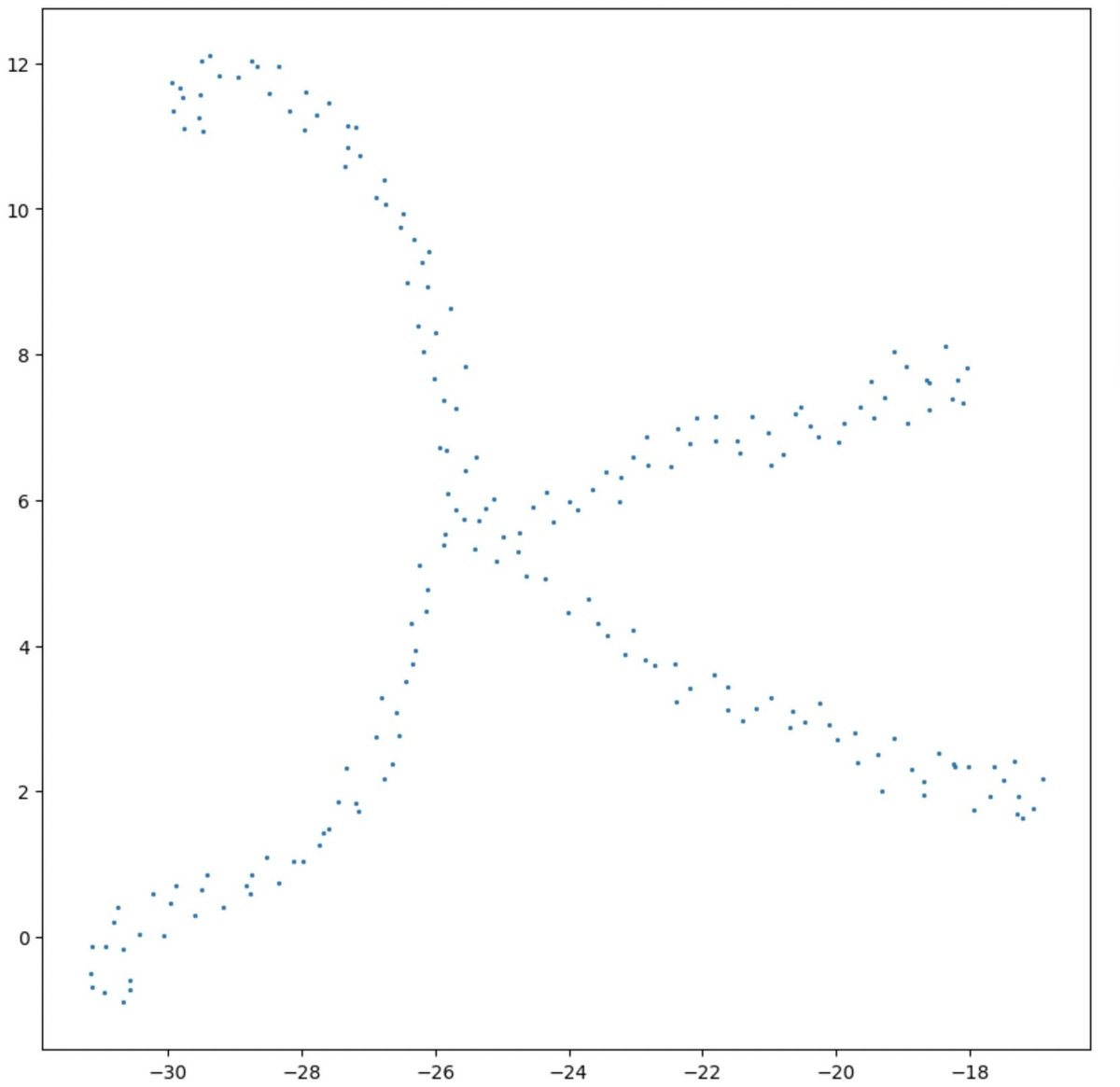
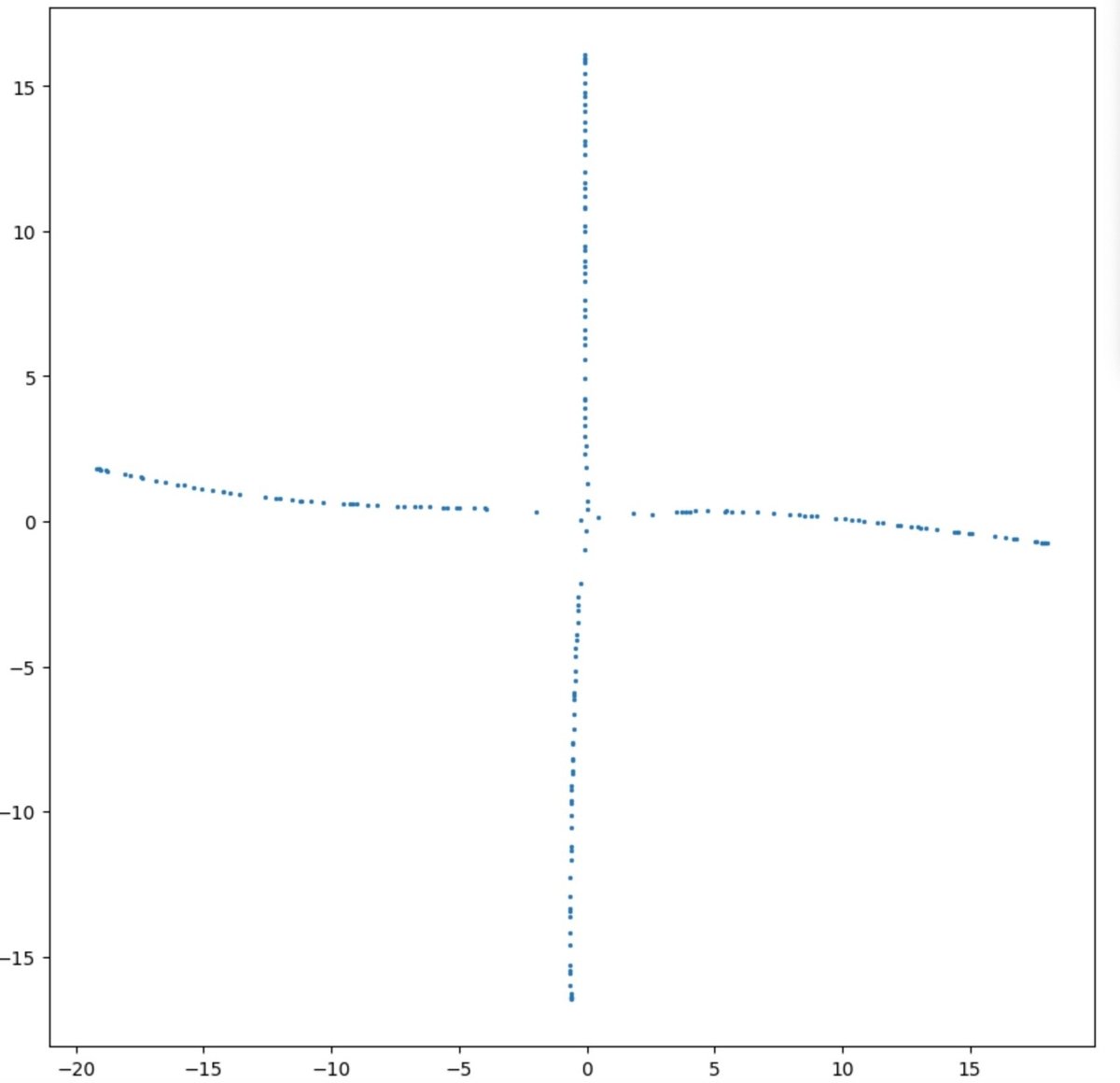
一方でPaCMAPはこうなります。
UMAPは元々は真っ直ぐなはずの点の並びがふわっとしてしまっています。直交もまあまあ崩れちゃっていそうです。
一方でPaCMAPはかなり真っ直ぐっぽさも直交みも保っていることがわかります。
円、螺旋、曲面などで実験してみても面白いかもしれません。
誰かやって結果を教えてくれないかな…🤔
おしまい
ということでPaCMAPって次元削減の方法ってすごくない?って話をしてみました。高次元のいろいろな構造を保存して低次元に見せてくれる様子が伝わったでしょうか?
今回は数学的な中身に全然触れられなかったので、別の機会に紹介できたらと思います。(欲張ってると一生投稿できなくなっちゃいそうだったので😢)
最後まで読んでいただき、ありがとうございました!!!!!
