
数学Ⅲ「積分法」に手も足も出なくて困っている方へ…置換積分法や部分積分法もこれならできます
(微分法については、こちらのページをご覧ください。
数学Ⅲの「積分法」についてみていきましょう。
表題(「積分法」に手も足も出なくて困っている方へ…置換積分法や部分積分法もこれならできます)のとおり、初級者向けのものです。
また、今回は「不定積分」の範囲にしぼり、積分の基本計算方法を勉強していきます。
「置換積分法」や「部分積分法」が、あまりよくわからなくて困っている人も多いと思います。
そういうみなさんに向けて、これらの積分のやり方を身に付けてもらうことを主眼にしております。
取り扱い問題は、こちらからダウンロードできます。
解答は、こちらです。
解説動画は、埋め込みのものの他に、その上に再生時間をのせリンクを貼っておきます。
リンクは別タグで開かれますので、使いやすい方でどうぞ。
それでは、始めましょう。
1.基本の積分法
ここは、簡単に確認だけです。
解説動画では、基本的な積分法の解説を加えてから、各問の解答を示しています。大切なところは、この解説指示内でも文章で書きおこしているので、2回目からは、こちらだけみれば大丈夫でしょう。
⑴ 積分の基本的性質
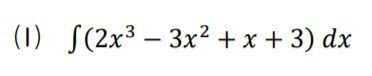
数学Ⅱの段階で、nが正の整数のとき

ということを勉強しました。これは微分の逆の操作なので大丈夫でしょう。
また、「x」を微分すると「1」になるのと反対で、「1」を積分すると「x」になります。これは上の公式で「n=0」のときなので、n=0 のときも、この公式に含まれます。
また、次のような公式も数学Ⅱの段階で確認しました。

これは単に、例えば「2x³ -3x² +x +3」を積分する際、
「2x³」と「-3x²」と「x」と「3」を、それぞれ積分してたせばよいということです。
さらには、「2x³」を積分する際、「2 ×(関数「x³」を積分したもの)」と考えて処理すればよいということです。
動画では、わかりやすくするため数学Ⅱの範囲の積分で説明しています。
ここは、大丈夫という人は、みなくてもよいでしょう。
数学Ⅲに入り、三角関数や指数関数などの積分も出てきますが、基本的にはこの考え方でこなせる、ということです。
例えば、(ここでは計算しませんが)・・・
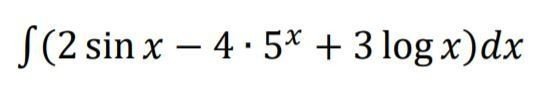
・・・と、いうような不定積分も・・・

・・・という形だと考え(計算のときに、この1行は、はさまなくてもよいでしょう。頭の中で処理できればよいです)、「∫sinx dx」や「∫logx dx」などを、それぞれ考えてゆけばよい、ということになります。
とても大切な内容なので、確認しておきましょう。
⑵ 「xの累乗」型のの不定積分
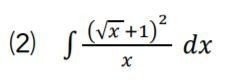
数学Ⅲの「微分法」で、xについている指数が正の整数のときだけでなく、負の整数を含め整数全体で、また、小数や分数を含め有理数全体で、さらには根号を使って表す数などの無理数でも・・・
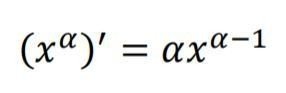
・・・という微分についての公式が成り立つことを確認しました。
よって、その逆の操作である積分でも、αを実数として・・・

・・・という公式が成り立ちます。
しかし、α=-1のとき「α+1」は0になってしまうので、この公式は適用できません。
α=-1のとき、xは逆数になります。
なので、(logx)を微分したとき、xの逆数になることから、次の形になります。
真数条件で、必ず正の数になるので絶対値が必要なことに注意しましょう。

α=-1のときの積分法については、動画の中で補足します。
⑶ 三角関数の不定積分1
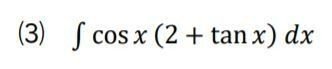
「sinx」を微分すると「cosx」、「cosx」を微分すると「-sinx」になりました。
よって、「sinx」は積分すると、(微分すると「sinx」になるようにと考えて、)「-cosx」・・・
「cosx」を積分すると、(積分して「cosx」になるようにと考えて、)「sinx」になります。
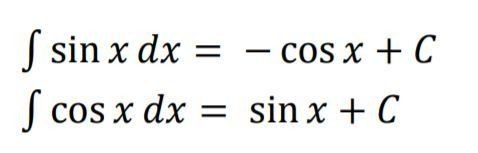
(Cは積分定数ですが、くどくなるので、これから先は公式の紹介のときは、特に断らないことにします。)
確認問題です。
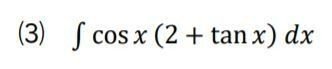
上でみた、積分法の2の性質は、わりと大切で、あのような形に持ち込めれば、それにこしたことはありません。
ここでも、分配してそうならないか?から考え始めています。
動画の中で説明していますが、tanxの性質から、tanxにcocxをかけると(分母が払えて)sinxになる、というのは、すぐにみえるといいです。
⑷ 三角関数の不定積分2
また、・・・
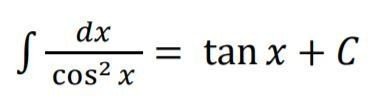
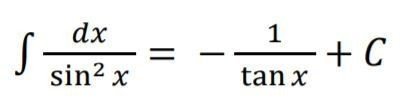
・・・という公式もあります。
こちらは、文だけでは説明が難しいので、解説動画の方で紹介します。
微分から説明します。
みなさんも、微分から自分でこの公式をおこせるようにしておきましょう。
では、これも簡単な問題で確認しておきましょう。
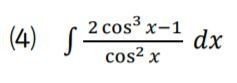
なお、「tanx」の積分については、置換積分法を使うので、後述します。
⑸ 指数関数の積分法
自然対数 e のx乗は、微分しても同じ形になるので、積分のときも同じです。
定数のx乗の場合の積分の形は覚えづらいですね。
やはり、微分から自分で起こせるようにしておく必要があります。
こちらは、動画で解説します。(e の場合もついでに解説します。)
こういう証明も、自分でできるようにしておかないと、なかなか定着しないので、しっかり練習しておきましょう。
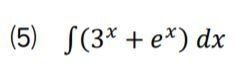
問題自体は公式にあてはめれば簡単ですが、公式にあてはめて何とかする・・・で通用する分野でもありません。
自分に厳しく、とりくんでいきましょう。
なお、対数「logx」の積分については、部分積分法を使って計算するので、そこで確認します。
2.置換積分法(基本)
・・・と、その前に…
「微分法」の段階で不安のある方もいるかもしれません。
すべて、さかのぼるのも非効率ですが、とりあえず「合成関数の微分法」は大切です。(これが、できないと積分した後に確かめができませんからね。)
「(1かたまりと思って微分)×(中身の部分)」という感覚が、まだつかめていない方は、こちらの動画からご覧ください。
「2.置換積分法(基本)」であつかう問題は、教科書などで・・・
「f (ax+b) の不定積分」などの名前であつかわれているものです。
ふつう、これくらいは文字に置き換えないでこなそうよ…と、されるところです。
でも、いまいちピンとこない、という人もいるかと思います。
最初は、文字に置き換えて計算してみましょう。
また、ここで説明するのは置換積分法の基本ですから「置換積分」がよくわからないという方は、ここからはじめるといいでしょう。
「置換積分法」の基本的な考え方がつかめます。
そして、この考え方さえつかめれば、置換積分法はできるようになります。
解説動画では、まず文字で置き換えた積分法を紹介し、その後、文字で置き換えないでこなす考え方を紹介します。
これから先を考えると、やはり置き換えないで積分できないと、つらくなってきます。
でも、慣れてしまえば、わりと簡単です。
「(1かたまりと思って積分)×(微分したときよぶんに出てくるものを消す)」・・・この感覚が、つかめれば大丈夫です。
それでは問題をみていきましょう。
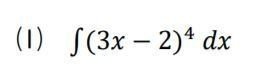
⑴ この段階で、わざわざ文字で置き換えなくてもいいかな?・・・と思えるかもしれません。置換積分法の確認のつもりで置き換えてみましょう。
「3x-2」を1かたまりととらえ、「t=3x-2」とおきます。
この式の両辺を微分すると、左辺はtという式をxで微分したということで、dt/dx と表されます。
この dt や dx は、等式のように処理ができ、これらを使って、もともとのxについての不定積分の式を「tについての」不定積分の式に置換できます。
これが、置換積分法です。
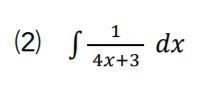
⑵ 対数が出てくるので、もう1回だけ文字で置き換えて解いてみましょう。よい確認になります。
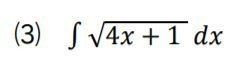
⑶ さすがに、もう大丈夫だと思うので、今回は最初から文字で置き換えないで解いてみます。意味さえとれていれば、置き換えない方が、よっぽどすっきりと解けます。
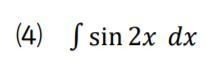
⑷ 三角関数です。置き換えない方がいいですね。
「(1かたまりと思って積分)×(微分したときよぶんに出てくるものを消す)」・・・で、サラッと解けます。
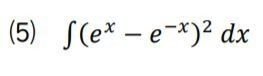
⑸ このままでは進まないので、2乗の展開からはじめましょう。
積分できる関数だけの多項式になるので、積分が進められます。
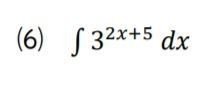
⑹ 指数関数は、やっかいそうにみえますね。
でも、同じように扱えます。
3.置換積分法
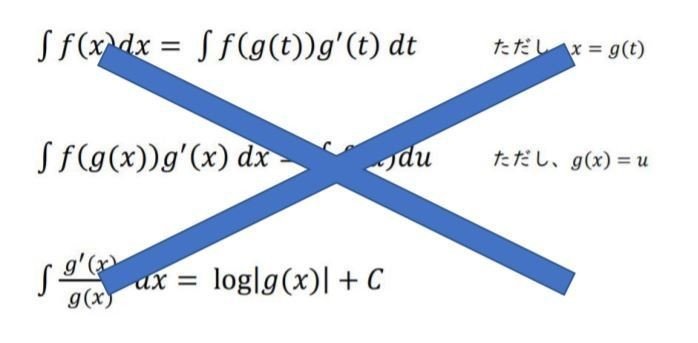
公式のようなものとして、教科書などで・・・

・・・このようなものが、紹介されています。
でもこれって・・・ちょっと何言ってるのかのか?・・・わからないですよね。
わからないものは、しかたがありません。
みなかったことに、しましょう。
解き方を「技」として身に付けていけば、大丈夫です。
そこで、活きてくるのが置換積分法です。
式を文字で置き換えましょう。
どの式のどの範囲を文字で置けばよいか?最初はわからないかもしれません。
でも、わからなかったら、適当にどこかおいてみればよいだけです。
それでダメだったら、別なところを置いて試す、・・・それがダメだったら、また・・・というふうに試行錯誤を繰り返せばいいのです。
しだいに計算の先を読み、すんなり適切なものをみつけられるようになります。
むしろ、よっぽどの天才でもない限り、最初からショートカットで正しい解法で進める、と思っている方が甘いです。
とにかく、練習が大切です。
それでは例題から、みてみます。

「5-x」を1かたまりと考えて、「t=5-x・・・①」とおきます。
(5-x)⁴ はtを使ってt⁴ と表されますし、①を変形すれば、xもtを使って表すことができます。
また、①の両辺をxについて微分することで、dx も dt で表すことができます。
これらを使い、もとの式がtについての不定積分に置き換えられました。
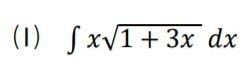
⑴ この問題なんか、根号の中身だけ tとおいても、根号全体をtとおいても、計算できます。悩む前にやってみればよい、という好例ですね。
動画では、どちらの解法も示します。確かめ算もしておきましょう。
確かめ算は、答えにめどがついている計算なので、計算力を高めます。
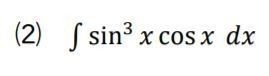
⑵ 発想としては、cosxの方を文字で置いてもしかたないので、sinxの方を文字で置く・・・くらいで、解けます。
「t=sinx」とおいた式の両辺を微分することで、「dt = cosxdx」という情報が得られます。
もとの式にも「cosxdx」という部分があり、まとめて dt と置き換えられます。これで、tについての不定積分になります。
なお、sinxは微分するとcosxになるというとみこして処理しろ、・・・というのが、上で紹介した公式の内容です。
あの公式を覚えてあてはめる・・・というのは、ものすごく非効率的ですが、ある程度は先はみこして、「sinを文字で置けば、微分してcosが出てくるので、もとの式のcosも、さばけるだろうな・・・」と、考えられるといいです。
これは、最初からできなくてもいいです。
たくさん練習して、少しずつ慣れていきましょう。
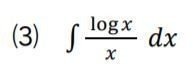
⑶ logxは微分するとxの逆数になるので、うまく進みそうです。
(なお、この問題で分母の方を文字で置いても、1歩も進みませんよね。文字が入れ替わるだけです。)
logxを文字で置けば、微分してxの逆数が出てきますよね。
もとの式の分母のxも、きっちりさばけます。
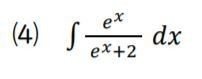
⑷ 分母と分子、どちらが微分したら簡単になるか?という発想でもいいでしょう。
分子は微分しても変わりませんが、分母は微分すると定数の部分が消えます。この「定数の部分が消える」というのは、わりと大切な視点です。
なお、これも上記の公式でいうと、「分母を微分すると、分子と同じ形になることを、確認して・・・」というものにあたります。
やはり、ああいう公式に頼らない方がいいですね。
「技」を増やしていく、という意識で勉強していくといいでしょう。
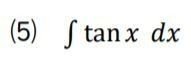
⑸ 三角関数「tanx」の積分は、置換積分法で求められます。
まずは、tanxをcosxとsinxに分解してみましょう。
分母の cosxを文字で置けば、微分して sinxが出てくるので、分子の sinxも、きっちりさばけます。
「tanxの積分は、置換積分法を使う」ということは、覚えておいたほうがよいでしょう。
4.部分積分法

こちらは、この公式が重要です。
必ず、自分でも1度証明してみて、いつでも導けるようにしておきましょう。
「f(x)×g(x)」を微分し、その両辺を積分することで導けます。
それでは、問題演習を進めましょう。
どちらを f(x) にして、どちらを g'(x) とすればよいか、わからない・・・なんて、お悩みはあり得ないですよね。
たかだか2拓です。
片方試してダメだったら、もう片方を試してみればいいだけの話です。
f(x) や g(x) 、また f'(x) や g'(x) が、ゴチャゴチャしてよくわからなくなる、ということはあると思います。
解説動画の中でもやっていますが、ノートの別のところで、みやすいように整理するとよいです。整理の仕方を、参考にしてください。
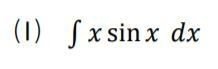
xを積分すると1になるから、簡単になりますね。こちらを f(x) としましょう。
g'(x) がsinxになります。g(x) は、微分して sinxになるものと考えるといいでしょう。
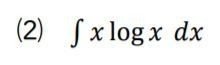
今度は、logxを g'(x) としてしまうと、微分して logxになるものは、すぐに出てこないので、進みません。
logxを f(x) とすれば、微分してxの逆数になるので、式も簡単になり、計算が進みます。
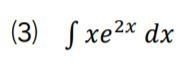
「e の 2x 乗」の方の積分を、上手にこなす必要があります。
そこらへんに不安がある方は、この解説の「2.置換積分法(基本)」に、お戻りください。
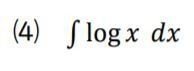
対数関数(logx)の積分は、部分積分法で処理します。
「logx」を「1×logx」と考え、「1」の方を g'(x) とします。
「tanxの積分は、置換積分法で」・・・と同じように、
「log xの積分は、部分積分法で」
さらには、「1×logx」と考える、ということは、覚えておくとよいでしょう。
以上です。ありがとうございました。
コメントなどいただけると、とてもうれしいです。
「こういう教材があったらいいな」のようなご意見でも、助かります。
執筆:井出進学塾(富士宮教材開発) 代表 井出真歩
井出進学塾のホームページは こちらをクリック
無料体験授業も、受付中です。
富士宮教材開発のホームページは こちらをクリック
各種教材を、準備しております。
note上に「高卒認定対策 特設サイト」もたちあげています
