
完全数と等差数列の関係
完全数とは
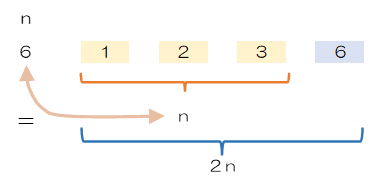
完全数とは、自身が自分自身を除く正の約数の和に等しくなる正の整数のことを指します。1番小さな完全数は6になりますが、n=6について自身6以外の約数は1,2,3となり、その合計は6になります。このため、正の整数nに対して正の約数の合計が2nになるものと考えた方が分かりやすい場合もあります。
完全数は小さい順に、6,28,496,8128,33550336,8589869056,137438691328と続きます。
完全数と等差数列
完全数と等差数列とは深い関係があります。例として、次の計算をしてみます。
(1) 1から3の合計
(2) 1から7の合計
(3) 1から31の合計
(4) 1から127の合計
(5) 1から8191の合計
(6) 1から131071の合計¶
(7) 1から524287の合計
def sumup_1(num):
total = 0
for i in range(1,num+1):
total+=i
return total
l_1=[3,7,31,127,8191,131071,524287]
print([sumup_1(num) for num in l_1])
#[28, 496, 8128, 33550336, 8589869056, 137438691328]完全数であれば、ある整数までの初校1、交差1の等差数列の合計になりそうです。
整数を3乗する数列との関連
さらに、3乗についての数列との関連も興味深いものがあります。例として次の計算をします。
(1) $1^3$から$3^3$の奇数の3乗の合計
(2) $1^3$から$7^3$の奇数の3乗の合計
(3) $1^3$から$15^3$の奇数の3乗の合計
(4) $1^3$から$127^3$の奇数の3乗の合計
(5) $1^3$から$511^3$の奇数の3乗の合計
(6) $1^3$から$1023^3$の奇数の3乗の合計
def sumup_3(num):
total = 0
for i in range(1,num+1,2):
total+=i**3
return total
l_2=[3,7,15,127,511,1023]
print([sumup_3(num) for num in l_2])
#[28, 496, 8128, 33550336, 8589869056, 137438691328]はじめの6以外、完全数は奇数を3乗した数列の合計として表すことができます。
詳しくは、次をご参照ください。
