＃5良問日誌〜1991 名古屋大文系③

⚡️ツナはる⚡️

はじめに

前回の記事はこちらから

ここから本格的に1990年代の問題を取り上げる。
今回の問題は見た目からウッとなる問題だが、そのような問題をどのような思考で解くのかを覚えていって欲しい。
今回は1991年名古屋大の問題だが、1991年名古屋大文系②も良問であるため、是非解いてみて欲しい。(下のツイートがとても参考になります)

筆者の実績

京都大学入試実戦模試(夏) 偏差値79.6
京都大学オープン模試(夏) 偏差値75.2
京都大学入試実戦模試(秋) 偏差値74.2
阪大入試実戦模試　数学全国2位
その他全国模試では常に偏差値70↑をキープ


問題



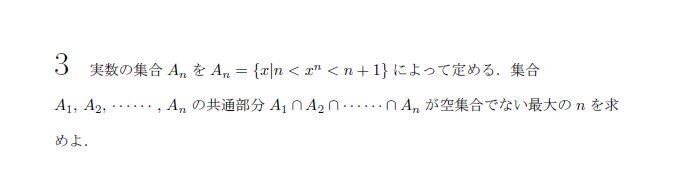
問題方針

$${n}$$絡みでよくわからない場合に大事なのは「実験」である。

$${n=1}$$ のとき $${1 < x < 2}$$

$${n=2}$$ のとき $${2 < x^2 < 3}$$

$${n=3}$$ のとき $${3 < x^3 < 4}$$

$${n=4}$$ のとき $${4 < x^4 < 5}$$

$${n=5}$$ のとき $${5 < x^5 < 6}$$

$${n=6}$$ のとき $${6 < x^6 < 7}$$

試しに$${A_1}$$と$${A_2}$$について調べてみよう。
$${A_1}$$ と$${A_2}$$を比べるために$${x^n}$$の$${n}$$を揃える。
$${A_1 = 1 < x < 2 = 1^2 < x^2 < 2^2 }$$
$${A_2 = 2 < x^2 < 3 }$$
とすると確かに共通部分があることがわかった。
これを$${A_3,A_4,A_5・・・}$$で調べると$${n=4}$$が答えであることが予測できる。
それを解答にすれば良い。(解答の作成方法は解答で)

それと他に$${logx}$$の微分を用いる別解(マクローリン展開利用)も紹介する。理系は参考にしてほしい。

今回の解答はあまり自信がないので誤植があったら指摘お願いします。

解答


$${(i)}$$

$${A_3 = 3 < x^3 < 4 = 3^5 < x^{15} < 4^5}$$

$${A_5 = 5 < x^5 < 6 = 5^3 < x^{15} < 6^3}$$

$${3^5 = 9×3^3 , 6^3 = 8×3^3 \\ \because 6^3<3^5}$$

$${\therefore A_3∩A_5}$$は空集合である。

$${(ii)}$$

$${A_1 = 1 < x^1 < 2}$$

$${= 1 < x^{12} < 4096  \land  x > 0}$$

$${A_2 = 2 < x^2 < 3}$$

$${= 64 < x^{12} < 729}$$

$${A_3 = 3 < x^3 < 4}$$

$${= 81 < x^{12} < 256  \land  x>0}$$

$${A_4 = 4 < x^4 < 5}$$

$${= 64 < x^{12} < 125}$$

$${\therefore A_1∩A_2∩A_3∩A_4}$$

$${= 81 < x^{12} < 125  \land  x > 0}$$

$${\therefore A_1∩A_2∩A_3∩A_4}$$は空集合ではない。

$${(i),(ii)}$$より、$${A_1∩A_2∩…∩A_n}$$が空集合ではない最大の$${n}$$は$${4}$$である。



解答(理系向け)



$$
n<x^n<n+1 
$$


$$
\iff \dfrac{1}{n}･logn<logx<\dfrac{1}{n}･log(n+1)
$$


ここで、$${f(x)=\dfrac{1}{n}･logn}$$とおくと


$$
f’(x)=-\dfrac{1}{n^2}･logn + \dfrac{1}{n^2} 
$$


$$
=-\dfrac{1}{n^2}(-logn+1)
$$


よって、$${n=e}$$のとき$${f(x)}$$は最大値となる。
$${2 < e < 3}$$より、

$$
f(2)=log\sqrt{2} \\
f(3)=log3^\frac{1}{3} \\
1.41<\sqrt{2}<1.42 \\
1.44<3^\frac{1}{3}<1.45
$$


よって
$${n}$$が自然数のとき、$${f(x)}$$は$${log3^\frac{1}{3}}$$が最大値となる。

また、$${g(x)=\dfrac{1}{n}･log(n+1)}$$とすると、


$$
g’(x)=-\dfrac{1}{n^2}･log(n+1)+\dfrac{1}{n}･\dfrac{1}{n+1} 
$$


$$
=\dfrac{1}{n}-(\dfrac{1}{n}･log(n+1) + \dfrac{1}{n+1})
$$


$${n=1}$$のとき

$$
g’(x)=-log2+\dfrac{1}{2} 
$$


$$
=log\dfrac{1}{2}+log\sqrt{e} 
$$


$$
=log(\dfrac{\sqrt{e}}{2})<0
$$


$${n\geqq 2}$$のとき


$$
g’(x)=\dfrac{1}{n}(-\dfrac{1}{n}･log(n+1)+\dfrac{1}{{n(1+\frac{1}{n})}} )
$$


$$
=\dfrac{1}{n}(-\dfrac{1}{n}･log(n+1) 
+\dfrac{1}{n}･(1-\dfrac{1}{n}+\dfrac{1}{n^2}-\dfrac{1}{n^3}+・・・) 
$$


$$
=\dfrac{1}{n^2}(ｰlog(n+1)+1-\dfrac{1}{n}+\dfrac{1}{n^2}・・・)<0
$$

よって、$${log3^\frac{1}{3} < \dfrac{1}{n}･log(n+1)}$$を満たす
最大の$${n}$$をもとめればよい｡


$$
1.44<3^\frac{1}{3}<1.45 
$$


$$
1.49<5^\frac{1}{4}<1.5 
$$


$$
1.43<6^\frac{1}{5}<1.44
$$


よって､求める最大の$${n}$$は$${4}$$

この記事が気に入ったらサポートをしてみませんか？