もっと使えるAUC〜ROCカーブを利用してよりよいモデルを選ぼう
ヒューマノーム研究所・代表の瀬々です。
今回は、機械学習モデルを作成したあと、そのモデルの性能を評価する指標・ROCカーブ (Receiver Operating Characteristic curve)とAUC(Area Under the Curve)について解説します。AUCの計算のもととなるROCカーブの形から、よりよいモデルはどれなのか?を読み解く方法もご紹介しますので、ぜひ最後までご覧ください。
モデル評価に使われる指標について〜精度とAUC
AUCは、「故障有り」「故障無し」を予測するモデルのように、2つのクラスのどちらにあたるかを予測するモデルの評価時によく用いられる指標です。
モデルの評価でよく用いられる指標に精度・正答率(Accuracy:正答数/全数)があり、これとAUCは、「似たようなもの」と思われがちですが、実は両者が意味するところは大きな差があります。
特にAUCは、計算のもとになるROCカーブをしっかり見ることで、機械学習のモデルを適切に評価するための判断材料として活用できます。今回の記事(機械の故障を判定するAIモデルの評価)で用いるROCカーブを作成する際に必要となる指標は以下の通りです。
感度:壊れている機械(見つけたい物)のうち、壊れていると予測した機械の割合
偽陽性率:壊れていると予測したが、本当は正常だった機械の割合(1−特異度も同じ値)
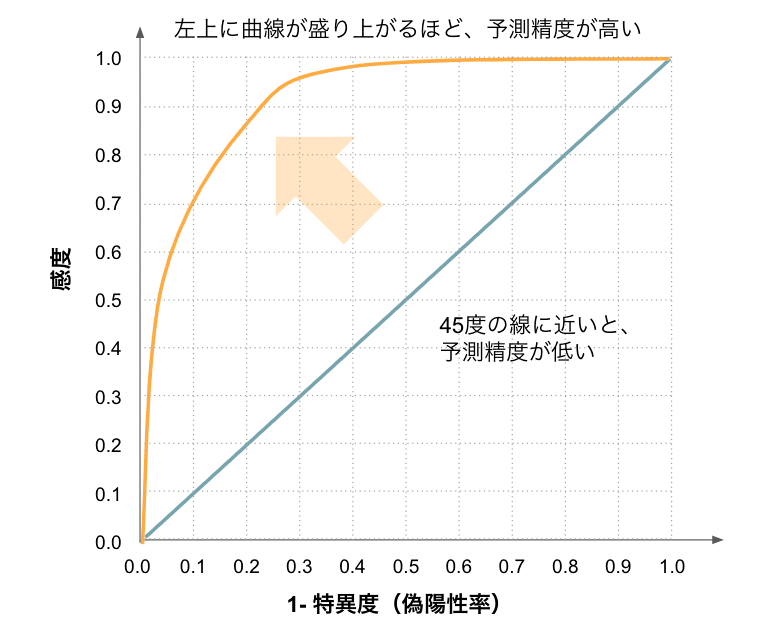
ROCカーブは、感度を縦軸に、偽陽性率を横軸にとったグラフです(図1)。カーブが左上に偏っているほど、よい精度のモデルと言えます。

ROCグラフについては下記の記事でも詳しく説明しています。よろしければご覧ください。
AUCの計算方法とROCカーブの描き方
まず、AUCの計算方法とROCカーブの描き方をおさらいします。ご存知の方は、次の項目まで飛ばしていただいて構いません。
AUCの計算方法
AUCはROCカーブの下の面積を表す値です。値が大きいほど精度の良いモデルと言えます。下の例では、緑の線がROCカーブを示します。全部で100マスのうち、薄緑で塗られた91マスがROCカーブの下に存在するため、AUCは0.91となります(図2)。

ROCカーブの描き方
ここでは、20台の機械を対象として、これらの機械が故障しているか?正常か?について予測したと仮定します。機械学習のモデルは予測の確信度(Confidence Score:予測がどのくらい正確であるかに関する推定値)を出力します。
この全20台の予測結果を、故障しているという確信度の高い方から順番に並べ、実際にそれらの機械に故障があったかどうか?についてもあわせて記載した表を以下に示します(図3)。全20台の内、故障ありは10台、故障なしは10台でした。

それでは、上記の図3のデータを使って、ROCカーブを描いていきます。
確信度1.0以上の機械を「故障あり」と判定した場合、最大でも確信度が0.98なので、 故障ありと判断される機械は1台もなく、全て「故障なし」と判断されます(図4 - ①の状態)。このとき、故障のない10台の内、1台も故障していると判定されてはいないので、偽陽性率は 0/10 = 0.0 となります。また、故障している10台の内、1台も故障ありと判定できていないので、感度は 0/10 = 0.0 です。これで、左下の① (0.0, 0.0) の点が描かれます。
次に、確信度0.98以上を故障ありと判定する場合を考えます。この場合は、機械番号1〜6までが故障あり判定となります(図4 - ②の状態)。故障のない10台のうち1台も故障有りとは判定されていないので、偽陽性率は0.0 。故障している10台中6台が見つかっているので、感度は 6/10 = 0.6。これで、②(0.0, 0.6) が描かれます。
同様に、確信度0.90以上で区切ると、偽陽性率0.1 (故障のない10台中1台が故障ありと判定されている)、感度0.6となり③が書かれます。0.80だと④になります。このようにして、ROCカーブを描くことができます(図4)。

ROCカーブが描かれたら、その下の面積を計算した値がAUCとなります。上記で説明した描き方から、確信度の高いところに「故障あり」が集まると、カーブが左上に偏り、AUCが大きくなります。確信度の高い順に並べたにも関わらず、故障ありとなしの順番がランダムに現れれば現れるほど、ROCカーブは角度が45度の線に近くなります(図5)。
同じAUCでも異なるROCカーブが描ける
AUCが同じ値であっても、状況によって使えるモデル、使えないモデルが存在します。
例えば、AUCが0.85 となったら、ROCカーブは一意に決まるでしょうか?答えはNOです。以下に、AUC0.85 の2つのROCカーブを描きました(図6)。AUCの値では差はつきませんが、ROCカーブは明らかに異なります。これは、何を意味しているでしょうか?

先のROCカーブの書き方に戻って考えてみましょう。オレンジの方は、X軸の偽陽性率が0.0の状態が長く、あるしきい値を境に偽陽性率があがっていきます。
つまり、確信度が高い方からサンプルを並べたとき、故障の有無が図7のように、確信度が高いところに実際に故障している機器が集中している一方、確信度が低いところにも故障している機器が含まれる状態を示します。

緑の方は、偽陽性率が高いとき、感度が低いので、オレンジのグラフ同様に確信度順に並べると図8のように、確信度の低いところに「故障なし」が集中している状態になります。しかし、確信度の高いところにも故障なしの機材が含まれています。

AUCの値は同じこの2つのグラフですが、どちらが良いのでしょうか? この良し悪しは状況によります。
オレンジの方は、確信度が高いところに故障している機器が少ないので、モデルが「故障あり」と予測した場合、必ず壊れているモデルが欲しい場合に適しています。しかし、確信度が低いところにも故障している機器があるため、故障を見逃す恐れがあることには注意する必要があります。
緑の方は、確信度が高いところにエラーが多いので「故障あり」と予測したとしても、故障がない場合がある(偽陽性が有る)状況ですが、故障は取りこぼさないモデルが欲しい場合に適しています。
機材の故障を予測する場合は、AIの予測結果に従って、予備の部品の発注などを考えたい場合が多いでしょうから、同じAUCであっても、緑の方のモデルが適しています。
AIモデルを比較する場合、精度やAUCなどの指標が高いモデルを選ぶことが多いですが、AUCの値だけでなく、ROCカーブも調査して、自身の目的に適しているか調べることで、現場の判断に即した機械学習モデルが構築できます。
簡単に確信度を計算して、ROCカーブを描く方法
以上、AUCの計算方法やROCカーブの描き方をご紹介しました。
評価指標の算出にあたり、Pythonのscikit-learnなどを用いた場合、AUCの計算まではすぐにできても、どのサンプルが、どれだけの確信度で予測されたのかの対応づけは、意外と面倒です。当社が開発するノーコードAI開発ツールのHumanome CatDataは、実際にデータ解析に携わってきたメンバーが開発しているため、このような「ちょっと面倒くさい作業を便利にする」有用な機能が備わっています。
CatDataは図9の様に、各サンプルの予測の値と確信度の値が、コーディングなしですぐに表示できます。今回紹介したような、一歩深いモデルの精度検証も非常に簡単です。是非おためしください。

ROCカーブに関する関連記事
AI・DX・データサイエンスについてのご質問・共同研究等についてはお気軽にお問い合わせ下さい!