
曲線運動におけるエネルギー保存
はじめに
高校物理では力学を一番はじめに習います.力学においては,簡単な状況設定でエネルギー保存を導出することができ,数学でいう定理に対応します.しかし,問題が複雑になる,あるいは熱力学などの分野に学習を進めると,エネルギー保存は定理というよりむしろ第一原理となります.議論の出発点としてエネルギーが保存するということを仮定するのです.
理論的に重要である一方で,高校物理の問題を解く上でも,エネルギー保存は必須です.特に力学においては,台の上に束縛された物体のなめらかな運動は頻出であり,通常はエネルギー保存と運動量保存が連立されます.台上面の形状が一般の曲線である場合,そこに束縛された運動を運動方程式から時間追跡するのは不可能だからです.
現在,曲線が特に直線である場合の物体と台のエネルギー保存の導出はネット上に多く存在しますが,曲線が一般の場合の証明はほとんどありません.そこで,一般曲線の場合にもエネルギー保存を証明しておくことに意義があると考え,記事にします.
導出は, デカルト座標と曲線座標に基づいた2つの方法でなされます.デカルト座標は,本記事では静止系に固定されています.一方で曲線座標は, 曲線に固定されており,時間と共に変化する直交座標です.合成関数の微分と,ベクトルの内積を理解していれば,読み進めることができます.
問題設定
さて,本題に入りましょう.図のように台上に束縛された質量$${m}$$の質点の運動を考えます.摩擦はないものとし,重力加速度を$${g}$$とします.質点は台から飛び出さないとします.
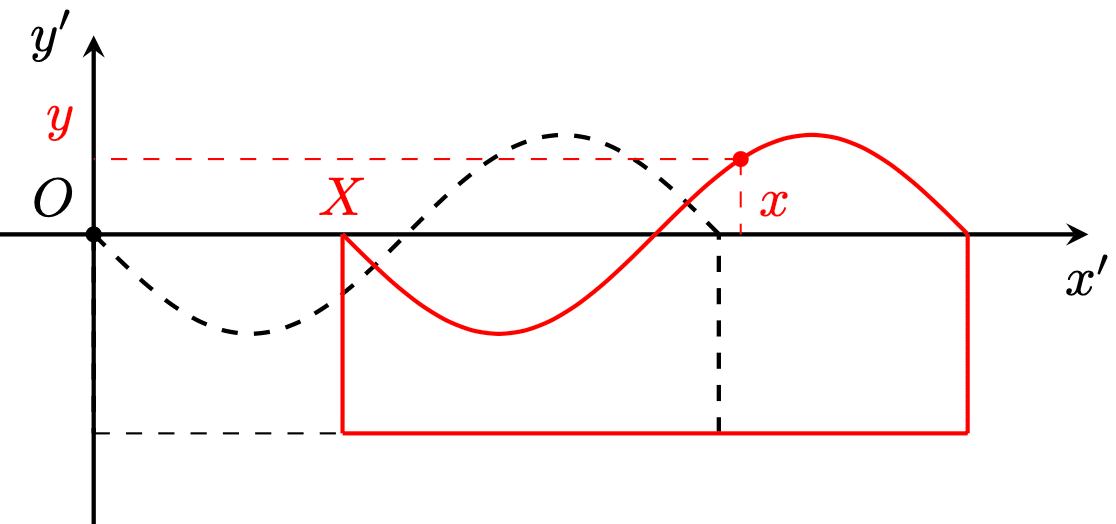
質点の位置を$${(x,y)}$$で,台の位置を$${X}$$で表します.時刻$${0}$$において,$${x=y=X=0}$$が満たされているとし,このときの台の関数形が$${f(x')}$$であったとします.時刻$${t}$$において,台の曲面は$${f(x')}$$を$${x}$$軸正の方向へ$${X}$$だけずらしたものになるので,その関数形は$${f(x'-X)}$$となります.これに$${x'=x(t)}$$を代入したものが$${y(t)}$$にならなければなりません:
$$
y=f(x-X).
$$
この関係は,質点が台の上を運動していることを表しているため,束縛条件と呼ばれます.
束縛条件を時刻$${t}$$で微分すると,合成関数の微分を用いて
$$
\dot{y} = f'(x-X)(\dot{x}-\dot{X})
$$
となります.$${'}$$は$${x-X}$$での微分を, $${\cdot}$$は時刻での微分を表しています.これは質点の台に対する相対速度が,曲線$${y' = f'(x'-X)}$$の$${x'=x(t)}$$における接線に平行であるということを意味しています.
小球の運動方程式をベクトルで表現すると,
$$
m\begin{pmatrix}
\ddot{x}\\ \ddot{y}
\end{pmatrix}
=
\begin{pmatrix}
N_{x}\\N_{y}
\end{pmatrix}
+
\begin{pmatrix}
0\\ -mg
\end{pmatrix}
$$
となります.ここで$${N_{x}}$$, $${N_{y}}$$はそれぞれ垂直抗力の$${x,y}$$成分です.今,摩擦は考えていないことから,ある点の垂直抗力と,その点における曲線の接線は直交します.
$$
\begin{pmatrix}
N_{x}\\ N_{y}
\end{pmatrix}
\cdot
\begin{pmatrix}
1\\
f'(x-X)
\end{pmatrix}
=0.
$$
曲線の接線は台に対する質点の相対速度に平行であったことを思い出すと
$$
\begin{pmatrix}
N_{x}\\ N_{y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\dot{x}-\dot{X}\\ \dot{y}
\end{pmatrix}
=0
$$
も言えます.垂直抗力は,台に対する質点の相対速度に直交します.
デカルト座標での議論
運動方程式の$${x}$$成分に$${\dot{x}}$$をかけたものと,$${y}$$成分に$${\dot{y}}$$をかけたものを足すと
$$
\begin{align*}
m(\dot{x}\ddot{x}+\dot{y}\ddot{y}) = N_{x}\dot{x}+N_{y}\dot{y}-mg\dot{y}
\end{align*}
$$
合成関数の微分を用いて整理すると
$$
\begin{align*}
\frac{d}{dt}\left(\frac{1}{2}mv^{2}+mgy\right) = \begin{pmatrix}N_{x}\\ N_{y}\end{pmatrix}\cdot \begin{pmatrix} \dot{x}\\ \dot{y}\end{pmatrix}
\end{align*}
\tag{1}
$$
となります.速さ$${v}$$を$${v=\sqrt{\dot{x}^{2}+\dot{y}^{2}}}$$で定義しました.右辺は一般に$${0}$$ではないことに注意しましょう.垂直抗力は台の曲線の接線に直交しているのであり,実際の運動曲線の接線には直交していないためです.したがって,台の上の物体だけを考えても,エネルギーは保存しません.$${M}$$が$${m}$$より十分大きく,近似的に$${\dot{X}=0}$$とみなせる場合には,垂直抗力は運動曲線の接線と直交し,したがってエネルギーは保存するとみなせます.
そこで,台のエネルギーも含めて考えましょう.台の運動方程式の両辺に$${\dot{X}}$$をかけると
$$
\frac{d}{dt}\left(\frac{1}{2}M\dot{X}^{2}\right)=-N_{x}\dot{X} \tag{2}
$$
となり,これと$${(1)}$$を合わせると
$$
\frac{d}{dt}\left(\frac{1}{2}mv^{2}+\frac{1}{2}MV^{2}+mgy\right)=
\begin{pmatrix}
N_{x}\\
N_{y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\dot{x}-V\\
\dot{y}
\end{pmatrix}=0
\tag{3}
$$
となります.$${V=\dot{X}}$$と定義しました.最後の等式では,垂直抗力と相対速度が直交することを用いました.結局,台と物体両方を一つの系とみなすと,そのエネルギーは保存することが言えます.
曲線座標での議論
前セクションでは,デカルト座標を用いてエネルギー保存を議論しました.言い換えれば,任意の時刻において共通の単位ベクトル
$$
\vec{e}_{x}=\begin{pmatrix} 1\\0\end{pmatrix},\vec{e}_{y}=\begin{pmatrix} 0\\ 1\end{pmatrix}
$$
を用いて運動方程式を成分表示したということです.それに対し,このセクションでは,運動曲線に接する単位ベクトル方向の運動方程式を導出し,そこからエネルギー保存を導出します.法線方向の運動方程式はエネルギー保存とは関係がないので,本記事では省略します.速度ベクトル$${\vec{v}}$$を用いて,接ベクトル$${\vec{e}_{\mathrm{T}}}$$を
$$
\vec{e}_{\mathrm{T}}=\frac{\vec{v}}{v}
$$
と定義します.
加速度$${\frac{d\vec{v}}{dt}}$$, 垂直抗力$${\vec{N}}$$, 重力$${m\vec{g}}$$の$${\vec{e}_{\mathrm{T}}}$$成分を計算すると
$$
\begin{align*}
\vec{a}\cdot\vec{e}_{\mathrm{T}} & = \frac{\vec{v}}{v}\cdot\frac{d\vec{v}}{dt}\\
\vec{N}\cdot\vec{e}_{\mathrm{T}} & = \frac{1}{v}(N_{x}\dot{x}+N_{y}\dot{y})\\
m\vec{g}\cdot{\vec{e}_{T}} &= \frac{1}{v}(-mg\dot{y})
\end{align*}
$$
となります.したがって物体の$${\vec{e}_{\mathrm{T}}}$$方向の運動方程式として
$$
m\vec{v}\cdot\frac{d\vec{v}}{dt} = \frac{1}{v}(N_{x}\dot{x}+N_{y}\dot{y})+ \frac{1}{v}(-mg\dot{y})
$$
が得られます.両辺に$${v}$$をかけて整理すると
$$
\frac{d}{dt}\left(\frac{1}{2}mv^{2}+mgy\right) = \begin{pmatrix} N_{x}\\ N_{y}\end{pmatrix}\cdot\begin{pmatrix} \dot{x}\\ \dot{y}\end{pmatrix}
$$
再び,右辺は一般には$${0}$$ではないことに注意します.台のエネルギーと仕事の関係$${(2)}$$まで考えれば$${(3)}$$が得られ,やはり系全体でエネルギーが保存することがわかります.
終わりに
曲線に束縛された質点の運動におけるエネルギー保存則を導出しました.この導出が入試で問われることはありませんが,なぜ系全体でエネルギーが保存するのか納得しておくと,物理の学習が進みやすいのではないでしょうか.このような高校物理の背景を今後も解説していく予定です.
