Derivation of the formula of conditional probability

The formula of conditional probability

The meaning:

• P: probability

• A | B: A given the event B has already occurred.

• A ∩ B: the joint event of A and B (look the image below)

The Venn diagram which shows the event of A ∩ B.

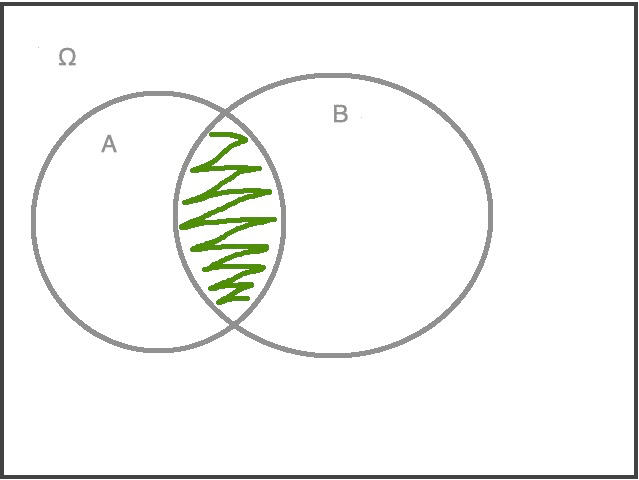
The derivation of the formula

So the meaning of P(A | B) is the probability of the event A given the information the event B has already happened.
Look at the image above. P(A | B) concerns the event A ∩ B, so the green area is considered in this situation. Because the event B has already occurred, the whole possible case is B (the sample space is narrowed to B). So the probability of P(A | B) is (using the definition of probability) :

(1) the probability in terms of A and B

The equation (1) if and only if (using algebra):

(2) where Ω is the sample space

And P(B) and P(A ∩ B) are (using the definition of probability):

(3)

(4)

So the equation (2) is transformed into the formula of the conditional probability by substituting it with (3) and (4). QED.