雑学マニアの雑記帳（その２２）那須の算額

栃木県那須町の那須歴史探訪館を訪ねた際、興味深い展示品を見ることができた。明和六年（１７６９年）三月吉日と日付が記された「算額」である。
算額とは、主に江戸時代に、和算（日本で発展した数学）の難問が解けたことを感謝するために、神社へ奉納した額のことである。算額には、その問題と答え、さらに解法の概要などが記される。あるいは、問題のみを記載して、その問題解決を祈願する目的で奉納されることもあったようだ。難しい問題を考案した者が、挑戦者を求めて広く問題を告知する意味もあったのだろう。
この那須の算額には、三つの問題と、その解法が書き綴られていた。独特の和算用語が使用されているため、内容の理解は容易ではないが、第２問については、なんとか概要を理解することができた。
その問題記述の部分には、下図のような図形が描かれていた。長方形の中に、図のように外接する三つの円が内接している。

ここで、
・長方形の縦横の長さの和は２４寸
・円の外積（円の外側のグレーの部分の面積）は８４．１２５（単位は未記載であるが「平方寸」と解釈するのが妥当であろう）であるとき、円の直径は何寸であるか、という問題だ。
　この算額では、問題の記述に続いて「答曰（答えていわく）円径五寸」と、解答が五寸であることが記されている。続いて４行ほどの簡単な解法が続く。典型的な算額である。
　さて、この問題を現代の数学で解いてみるとどうなるのか興味が沸いてくる。早速挑戦してみた。円の直径をＲとして、ピタゴラスの定理を活用するのが良さそうである。長方形の縦横の長さや、外積の情報を加味すればＲに関する二次方程式が完成する。詳細は省くが、次のような方程式である。

円径は正の数であることに注意して、二次方程式の解の公式を適用すれば、円径Ｒは次の通りとなる。

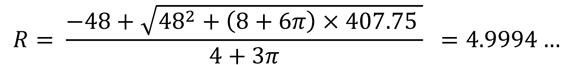
この計算では円周率として厳密な値を使用したが、仮に円周率π=3.14と仮定すれば、ちょうど円径R = 5.0となり、算額に記載された答えと完全に一致する。当時すでに、円周率として小数第二位まで正確な値が使用されていたようだ。
一方、この算額に記載されている解法であるが、もちろんピタゴラスの定理が使われた形跡はない。この算額ではそれを使わない別解が示されている。解法は概略のみの記載なので、思考の過程が詳らかではないのが残念であるが、四角形や円の面積の公式を用いて、基本的な幾何学的思考法で解いているように見える。最終的には、やはり二次方程式に帰着させて解いている。
面白いことに、その二次方程式の解き方自体については言及がない。調べてみると、当時は「算木」と呼ばれる木製の棒と、算盤（「そろばん」ではなく「さんばん」と読む。格子状の枠が書かれた板や布のことである。）を使って二次方程式を解く方法が存在していたらしい。そのため、方程式を解く部分についてはわざわざ記載しなかったのであろう。円周率に３．１４が使用されていたことも併せて、当時の和算のレベルの高さを改めて窺い知ることができた。
江戸時代の農村といえば、日々の農作業に追われて学問や趣味に時間を割く余裕など無かったものと勝手に想像していたが、このような幾何学の問題を考案したり解決したりするといった活動が行われていたとは驚きである。江戸時代の数学マニア達に拍手を送りたい。