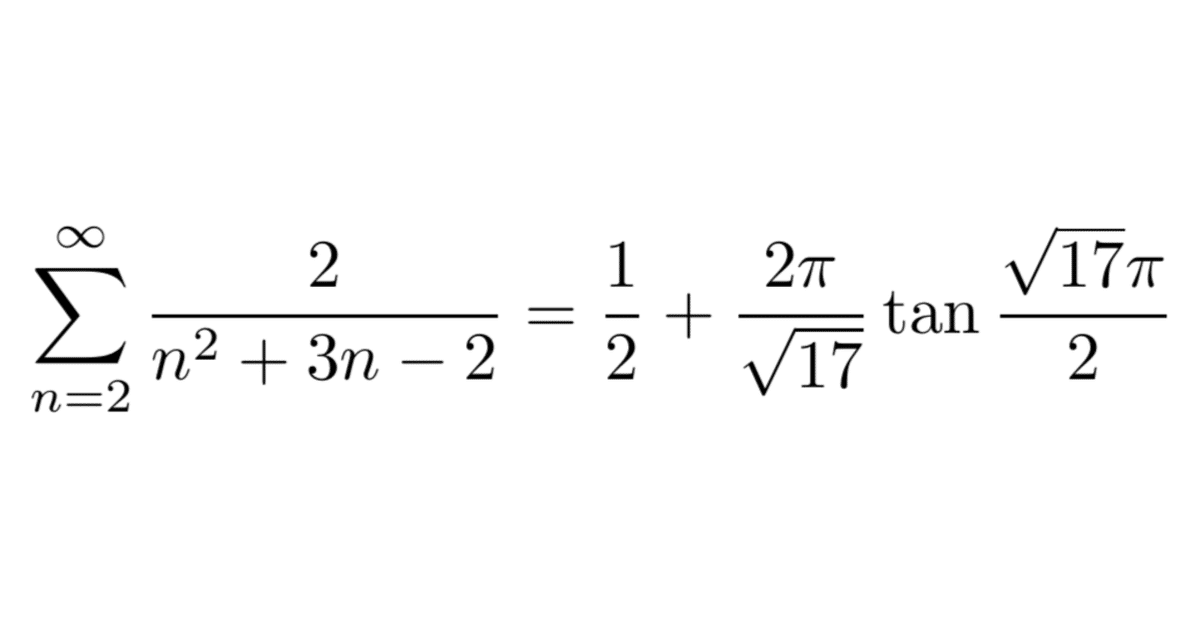
見出し画像

2025東京理科大で出題された無限級数（高校範囲外！？）

大澤裕一

2025/02/05(水)に実施された東京理科大理学部数学科の大学入試で、以下の無限級数を問う問題が出題されました（原題については、このnoteの下のほうに掲載しています）。

　　　　　　　　　$${S=\displaystyle \sum_{n=2}^{\infty} \frac{2}{n^2+3n-2}}$$

これを高校範囲で求めることは困難（≠不可能）であり、出題不備（出題ミス）かと思われます（理科大に連絡済みです）。

さて、その上で、この無限級数を求めましょう。いくつかの方法がありますが、ここでは$${\cos \pi x}$$の無限乗積展開
　　　　　　　　　$${\displaystyle \cos \pi x =\prod_{n=1}^{\infty } \left(1-\frac{x^2}{\left(n-\frac{1}{2}\right)^2}\right)}$$ …(1)
を用いて考えます（高校生でもギリギリ理解できる！？）。
ここで、$${M \leqq N}$$なる整数$${M,N}$$に対し、
　　　$${\displaystyle \prod_{n=M}^{N} A_n=A_M A_{M+1} A_{M+2}\cdots A_N、\prod_{n=M}^{\infty} A_n=\lim_{N \to \infty} \prod_{n=M}^N A_n}$$
です。
(1)が成り立つことは、$${\cos \pi x=0}$$となる$${x}$$が$${\displaystyle x=\pm \left(n-\frac{1}{2}\right)~(n=1,2,3,\cdots)}$$であること、および$${\cos 0=1}$$から理解（≠証明）できますね（雑に言えば「$${\cos \pi x}$$を$${x}$$の無限次の多項式とみなして因数定理や定数項を考える」ということ）。

(1)の両辺の$${\log}$$を取って両辺を$${x}$$で微分（右辺は項別微分）することで、
　　　　　　　　　$${\displaystyle \frac{-\pi\sin \pi x}{\cos \pi x} =\sum_{n=1}^{\infty }\frac{-2x}{\left(n-\frac{1}{2}\right)^2-x^2}}$$
です。従って、$${\displaystyle x \neq 0,\pm\left(n-\frac{1}{2}\right)~(n=1,2,3,\cdots)}$$のとき
　　　　　　　　　$${\displaystyle \sum_{n=1}^{\infty }\frac{1}{\left(n-\frac{1}{2}\right)^2-x^2}=\frac{\pi\tan \pi x}{2x}}$$ …(2)
が得られます。
■ちなみに、$${\sin \pi x}$$の無限乗積展開
　　　　　　　　　$${\displaystyle \sin \pi x =\pi x \prod_{n=1}^{\infty } \left(1-\frac{x^2}{n^2}\right)}$$
で同じことを考えると、以下が得られます。ここで、$${x}$$は整数でないとします。
　　　　　　　　　$${\displaystyle \sum_{n=1}^{\infty }\frac{1}{n^2-x^2}=\frac{1}{2x^2}-\frac{\pi\cos \pi x}{2x\sin\pi x}}$$
（この式の両辺で$${x \to 0}$$とすることで、$${\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}}$$が得られます！）


さあ、(2)を用いて$${S}$$を求めましょう。

　$${\displaystyle S=\sum_{n=2}^{\infty} \frac{2}{n^2+3n-2}=\sum_{n=2}^{\infty} \frac{2}{\left(n+\frac{3}{2}\right)^2-\frac{17}{4}}}$$
　　（$${n}$$を$${n-2}$$に置き換えて）
　　$${\displaystyle =\sum_{n=4}^{\infty} \frac{2}{\left(n-\frac{1}{2}\right)^2-\frac{17}{4}}=2\sum_{n=1}^{\infty} \frac{1}{\left(n-\frac{1}{2}\right)^2-\frac{17}{4}}-\sum_{n=1}^{3} \frac{2}{n^2-n-4}}$$
　　（(2)で$${\displaystyle x=\frac{\sqrt{17}}{2}}$$を代入して）
　　$${\displaystyle =2\cdot\frac{\pi}{\sqrt{17}}\tan\frac{\sqrt{17}\pi}{2}-\left(-\frac{1}{2}-1+1\right)}$$
　　$${=\displaystyle \frac{1}{2}+\frac{2\pi}{\sqrt{17}}\tan\frac{\sqrt{17}\pi}{2}}$$

キレイな（！？）結果ですね！

■この他に、ディガンマ関数（ガンマ関数の自然対数の導関数）やフーリエ級数を用いる方法などもあります。


■原題は次の通りです。今回の無限級数は(4)で問われています。問題の下に略解も載せています。

[問題]
座標平面内の点で$${x}$$座標、$${y}$$座標がすべて整数である点を格子点とよぶ。自然数$${n}$$に対して、以下の条件
　　　　　　　$${\displaystyle 0＜x \leqq \frac{n}{2}~ ,~ 0＜y \leqq \frac{n}{2}~ ,~ \frac{n}{2} \leqq x+y}$$
をすべてみたす格子点$${(x,y)}$$の個数を$${A_n}$$とする。このとき、次の問いに答えよ。
(1) $${A_5,A_6,A_7}$$を求めよ。ただし答のみでよい。
(2) 自然数$${n}$$に対して$${A_{2n+1}}$$を求めよ。また$${2}$$以上の自然数$${n}$$に対して$${A_{2n}}$$を求めよ。
(3) 自然数$${m}$$に対して$${\displaystyle \sum_{n=1}^m \frac{1}{A_{2n+1}}}$$を求めよ。
(4) $${\displaystyle \lim_{m \to \infty} \sum_{n=1}^m \frac{1}{A_{2n}}}$$を求めよ。
(5) $${\displaystyle \lim_{m \to \infty} \frac{1}{m}\sum_{n=m}^{2m} \log\frac{A_{4m+1}}{A_{2n+1}}}$$を求めよ。ただし対数は自然対数を表す。

[略解]
(1) 順に$${3,8,6}$$
(2) 順に$${\displaystyle \frac{1}{2}n(n+1),\frac{1}{2}(n^2+3n-2)}$$
(3) $${\displaystyle \frac{2m}{m+1}}$$
(4) $${\displaystyle \frac{1}{2}+\frac{2\pi}{\sqrt{17}}\tan\frac{\sqrt{17}\pi}{2}}$$
(5) $${2-2\log2}$$

[追記(2025/02/06(木))]
この件について、2025/02/05(水)に東京理科大に問い合わせをしていましたが、2025/02/06(木)に東京理科大学入試課よりお返事を戴きました。早い！最近は、「入試の不備に関する問い合わせの対応」がとても早く行われますね。適切なことです（対応内容が良いかどうかは別として）。

[追記(2025/02/21(金))]
2025/02/21(金)に東京理科大が「この問題は出題ミスである」と発表しました。
・問題文の条件に不足があり、高校の学習範囲内では解答不能な設問となった。
・当該問題については、全員正解として取り扱う。

https://www.tus.ac.jp/today/archive/2024/20250221_7126.pdf


いいなと思ったら応援しよう！